启用前?绝密
2009年贵州省黔东南州初中毕业升学统一考试
数学试卷
注意事项:
1、本卷共有三个大题,26个小题,满分150分,考试时间120分钟。
2、请用(蓝、黑)色墨水钢笔或圆珠笔直接在试卷上答题。
3、答题前务必将密封线内的项目填写清楚。并填上座位号。
一、单项选择题:(每小题4分,共40分)
1、下列运算正确的是( )
A.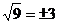 B.
B.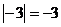 C.
C.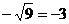 D.
D.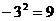
2、在下列几何图形中一定是轴对称图形的有( )

A.1个 B.2个 C.3个 D.4个
3、下列图形中,面积最大的是( )
A.对角线长为6和8的菱形; B.边长为6的正三角形;
C.半径为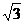 的圆;
D.边长分别为6、8、10的三角形;
的圆;
D.边长分别为6、8、10的三角形;
4、下面简举几何体的主视图是( )

正面 A B C D
5、抛物线的图象如图所示,根据图象可知,抛物线的解析式可能是( )
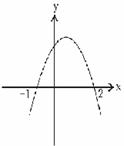
A.y=x2-x-2
B.y=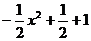
C.y=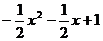 D.y=
D.y=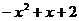
6、如图,在△ABC中,AB=AC,点D在AC上,且BD=BC=AD,则∠A等于( )
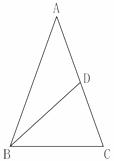
A.30o B.40o C.45o D.36o
7、方程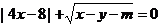 ,当
,当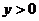 时,m的取值范围是( )
时,m的取值范围是( )
A.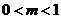 B.
B.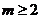
C.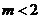 D.
D.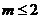
8、设矩形ABCD的长与宽的和为2,以AB为轴心旋转一周得到一个几何体,则此几何体的侧面积有( )
A.最小值4π B.最大值4π
C.最大值2π D.最小值2π
9、某校生物教师李老师在生物实验室做试验时,将水稻种子分组进行发芽试验;第1组取3粒,第2组取5粒,第3组取7粒……即每组所取种子数目比该组前一组增加2粒,按此规律,那么请你推测第n组应该有种子数( )粒。
A.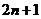 B.
B.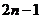 C.
C.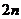 D.
D.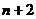
10、如图,在凯里一中学生耐力测试比赛中,甲、乙两学生测试的路程s(米)与时间t(秒)之间的函数关系的图象分别为折线OABC和线段OD,下列说法正确的是( )
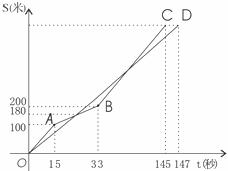
A.乙比甲先到终点;
B.乙测试的速度随时间增加而增大;
C.比赛进行到29.4秒时,两人出发后第一次相遇;
D.比赛全程甲的测试速度始终比乙的测试速度快;
二、填空题:(每小题4分,共32分)
11、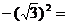 ___________
___________
12、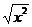 =___________
=___________
13、当x______时,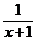 有意义。
有意义。
 14、在实数范围内分解因式:
14、在实数范围内分解因式: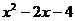 =__________________。
=__________________。
15、不透明的口袋中有质地、大小、重量相同的白色球和红色球数个,已知从袋中随机摸出一个红球的概率为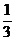 ,则从袋中随机摸出一个白球的概率是________。
,则从袋中随机摸出一个白球的概率是________。
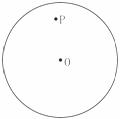
16、如图,⊙O的半径为5,P为圆内一点,P点到圆心O的距离为4,则过P点的弦长的最小值是_____________。
17、二次函数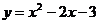 的图象关于原点O(0, 0)对称的图象的解析式是____________。
的图象关于原点O(0, 0)对称的图象的解析式是____________。
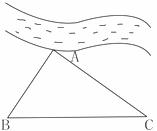
18、如图,某村有一块三角形的空地(即△ABC),其中A点处靠近水源,现村长准备将它分给甲、乙两农户耕种,分配方案规定,按每户人口数量来平均分配,且甲、乙两农户所分土地都要靠近水源(即A点),已知甲农户有1人,乙农户有3人,请你把它分出来。(要求:尺规作图,保留作图痕迹,不写作法,不要求证明)
三、解答题(8个小题,共78分)
19、(7分)先化简,再求值: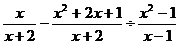 ,其中
,其中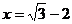 。
。
20、(7分)若不等式组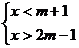 无解,求m的取值范围。
无解,求m的取值范围。
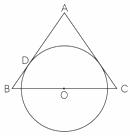
21、(9分)如图,△ABC为等腰三角形,AB=AC,O是底边BC的中点,⊙O与腰AB相切于点D,求证AC与⊙O相切。
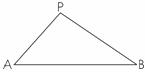
22、(9分)如图,在凯里市某广场上空飘着一只汽球P,A、B是地面上相距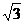 =1.732)
=1.732)
23、(10分)赏郎中学初三某班的同学积极参加体育锻炼,该班班长在篮球场对自己进行篮球定点投球测试,下表是他的测试成绩及相关数据:
第一回投球
第二回投球
第三回投球
第四回投球
第五回投球
第六回投球
每回投球次数
5
10
15
20
25
30
每回进球次数
3
8
16
17
18
相应频率
0.6
0.8
0.4
0.8
0.68
0.6
(1)请将数据表补充完整。
(2)画出班长进球次数的频率分布折线图。
(3)就数据5、10、15、20、25、30而言,这组数据的中位数是多少?
(4)如果这个测试继续进行下去,每回的投球次数不断增加,根据上表数据,测试的频率将稳定在他投球1次时进球的概率附近,请你估计这个概率是多少?并说明理由。(结果用分数表示)
24、(12分)如图,l1、l2、l3、l4是同一平面内的四条平行直线,且每相邻的两条平行直线间的距离为h,正方形ABCD的四个顶点分别在这四条直线上,且正方形ABCD的面积是25。
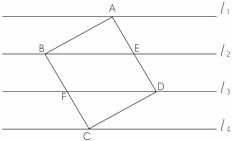
(1)连结EF,证明△ABE、△FBE、△EDF、△CDF的面积相等。
(2)求h的值。
25、(12分)凯里市某大型酒店有包房100间,在每天晚餐营业时间,每间包房收包房费100元时,包房便可全部租出;若每间包房收费提高20元,则减少10间包房租出,若每间包房收费再提高20元,则再减少10间包房租出,以每次提高20元的这种方法变化下去。
(1)设每间包房收费提高x(元),则每间包房的收入为y1(元),但会减少y2间包房租出,请分别写出y1、y2与x之间的函数关系式。
(2)为了投资少而利润大,每间包房提高x(元)后,设酒店老板每天晚餐包房总收入为y(元),请写出y与x之间的函数关系式,求出每间包房每天晚餐应提高多少元可获得最大包房费收入,并说明理由。
26、(12分)已知二次函数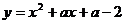 。
。
(1)求证:不论a为何实数,此函数图象与x轴总有两个交点。
(2)设a<0,当此函数图象与x轴的两个交点的距离为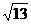 时,求出此二次函数的解析式。
时,求出此二次函数的解析式。
(3)若此二次函数图象与x轴交于A、B两点,在函数图象上是否存在点P,使得△PAB的面积为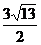 ,若存在求出P点坐标,若不存在请说明理由。
,若存在求出P点坐标,若不存在请说明理由。