2009年5月北京市朝阳区九年级综合练习(一)
数学试卷
第Ⅰ卷(选择题32分)
一、选择题(共8道小题,每小题4分,共32分)
1.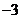 的绝对值是
的绝对值是
A.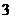 B.
B.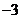 C.
C.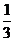 D.
D.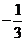
2.为积极转化奥运会、残奥会志愿者工作成果,完善和健全志愿者服务体系及长效机制,北京市将力争实现每年提供志愿服务时间11000万小时. 11000万小时用科学记数法表示为
A.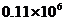 万小时
B.
万小时
B.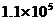 万小时
万小时
C.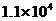 万小时
D.
万小时
D.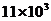 万小时
万小时
3.方程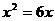 的解是
的解是
A.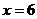 B.
B.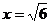
C.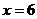 或
或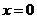 D.
D.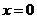
4.某市2008年4月的一周中每天最低气温如下:13,11,7,12,13,13,12,则在这一周中,最低气温的众数和中位数分别是
A.13和11 B.12和13
C.11和
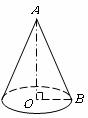
5.如下图,圆锥的高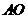 为12,母线
为12,母线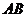 长为13,则该圆锥的侧面积等于
长为13,则该圆锥的侧面积等于
A. B.
B.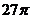 C.
C.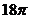 D.
D.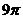
6.如图,△ABC内接于⊙O,∠C =45°,AB=2,则⊙O的半径为
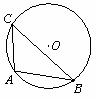
A.1 B.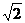 C.2 D.
C.2 D.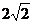
7.把4张形状完全相同的卡片的正面分别写上数字1,2,3,4,洗匀后正面朝下放在桌子上,随机从中抽取一张卡片,记下数字后放回,再随机从中抽取一张卡片,则两次抽取的卡片上的数字之和等于5的概率是
A.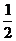 B.
B.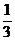 C.
C.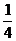 D.
D. 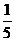
8.如下图,在直角梯形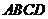 中,
中,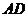 ∥
∥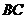 ,
,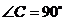 ,
,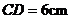 ,AD=
,AD=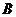 出发,点
出发,点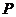 沿BA、AD、DC运动到点
沿BA、AD、DC运动到点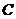 停止,点
停止,点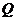 沿
沿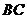 运动到
运动到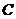 点停止,两点运动时的速度都是
点停止,两点运动时的速度都是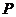 到达点
到达点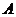 时,点
时,点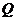 正好到达点
正好到达点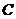 .设P点运动的时间为
.设P点运动的时间为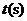 ,
,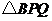 的面积为
的面积为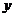
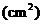 .
.
下图中能正确表示整个运动中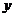 关于
关于 的函数关系的大致图象是
的函数关系的大致图象是
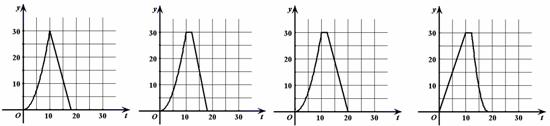
A. B. C. D.
第Ⅱ卷 (填空题和解答题,共88分)
二、填空题(共4个小题,每小题4分,共16分)
9.计算: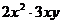 =
.
=
.
10. 因式分解: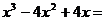 .
.
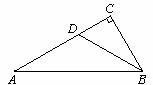
11.如下图,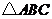 中,
中,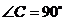 ,
,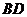 平分
平分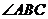 交AC于点D,若CD=6,则点D到AB的距离为
.
交AC于点D,若CD=6,则点D到AB的距离为
.
12.已知抛物线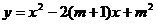 与x轴的两个交点的横坐标均为整数,且m<5,则整数m的值为
.
与x轴的两个交点的横坐标均为整数,且m<5,则整数m的值为
.
三、解答题(共13个小题,共72 分)
13.(本小题5分)
计算: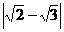 ― tan30° ÷
― tan30° ÷ 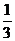 +
+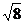 .
.
14.(本小题5分)
解方程: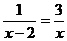 .
.
15.(本小题5分)
先化简,再求值: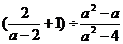 ,其中
,其中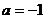 .
.
16.(本小题5分)
已知:如下图,AD∥BC,AD=BC,E为BC上一点,且AE=AB.
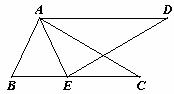
求证:DE=AC.
17.(本小题5分)
如下图,点 在反比例函数
在反比例函数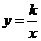 的图象与直线
的图象与直线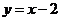 交于点
交于点 ,且
,且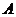 点纵坐标为1,求该反比例函数的解析式.
点纵坐标为1,求该反比例函数的解析式.
18.(本小题5分)
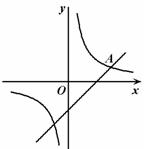
通常情况居民一周时间可以分为常规工作日(周一至周五)和常规休息日(周六和周日). 居民一天的时间可以划分为工作时间、个人生活必须时间、家务劳动时间和可以自由支配时间等四部分. 2008年5月,北京市统计局在全市居民家庭中开展了时间利用调查,并绘制了统计图:
 图①
图①
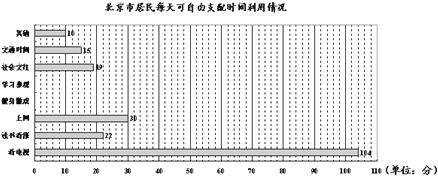
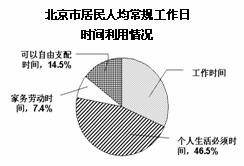
图②
(1)由图①,调查表明,我市居民人均常规工作日工作时间占一天时间的百分比为
(2)调查显示,看电视、上网、健身游戏、读书看报是居民在可自由支配时间中的主要活动方式,其中平均每天上网占可自由支配时间的12%,比读书看报的时间多8分钟. 请根据以上信息补全图②;
(3)由图②,调查表明,我市居民在可自由支配时间中看电视的时间最长. 根据这一信息,请你在可自由支配时间的利用方面提出一条建议:___ ____________.
19.(本小题5分)
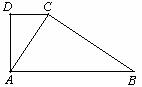
如下图,在梯形ABCD中,AB∥CD,∠D=90°,CD=4,∠ACB=∠D,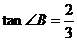 ,求梯形ABCD的面积.
,求梯形ABCD的面积.
20.(本小题5分)
改革开放30年来,我国的文化事业得到了长足发展,以公共图书馆和博物馆为例,
1978年全国两馆共约有1550个,至2008年已发展到约4650个. 2008年公共图书馆的数量比1978年公共图书馆数量的2倍还多350个,博物馆的数量是1978年博物馆数量的5倍. 2008年全国公共图书馆和博物馆各有多少个?
21.(本小题5分)
响应“绿色环保,畅通出行”的号召,越来越多的市民选择乘地铁出行,为保证市民方便出行,我市新建了多条地铁线路,与旧地铁线路相比,新建地铁车站出入口上下楼梯的高度普遍增加,已知原楼梯BD长
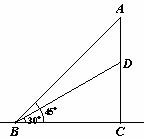
(结果保留整数,参考数据: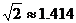 ,
,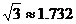 )
)
22.(本小题7分)
已知:在⊙O中,AB是直径,AC是弦,OE⊥AC于点E,过点C作直线FC,使∠FCA=∠AOE,交AB的延长线于点D.
(1)求证:FD是⊙O的切线;
(2)设OC与BE相交于点G,若OG=2,求⊙O半径的长;
(3)在(2)的条件下,当OE=3时,求图中阴影部分的面积.
23.(本小题5分)
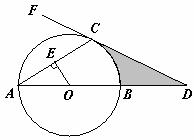
将图①,将一张直角三角形纸片ABC折叠,使点A与点C重合,这时DE为折痕,
△CBE为等腰三角形;再继续将纸片沿△CBE的对称轴EF折叠,这时得到了两个完全重合的矩形(其中一个是原直角三角形的内接矩形,另一个是拼合成的无缝隙、无重叠的矩形),我们称这样两个矩形为“叠加矩形”.
图① 图② 图③
(1)如图②,正方形网格中的△ABC能折叠成“叠加矩形”吗?如果能,请在图②中画出折痕;
(2)如图③,在正方形网格中,以给定的BC为一边,画出一个斜三角形ABC,使其顶点A在格点上,且△ABC折成的“叠加矩形”为正方形;
(3)如果一个三角形所折成的“叠加矩形”为正方形,那么它必须满足的条件是 ;
(4)如果一个四边形一定能折成“叠加矩形”,那么它必须满足的条件是 .
24.(本小题7分)
抛物线与x轴交于A(-1,0)、B两点,与y轴交于点C(0,-3),抛物线顶点为M,连接AC并延长AC交抛物线对称轴于点Q,且点Q到x轴的距离为6.
(1)求此抛物线的解析式;
(2)在抛物线上找一点D,使得DC与AC垂直,求出点D的坐标;
(3)抛物线对称轴上是否存在一点P,使得S△PAM=3S△ACM,若存在,求出P点坐标;若不存在,请说明理由.
25.(本小题8分)
图① 图②
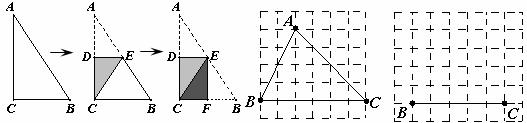
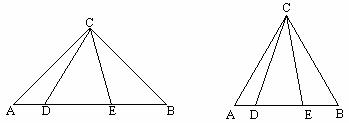
(1) 已知:如图①,Rt△ABC中,∠ACB=90°,AC=BC,点D、E在斜边AB上,且∠DCE=45°. 求证:线段DE、AD、EB总能构成一个直角三角形;
(2)已知:如图②,等边三角形ABC中,点D、E在边AB上,且∠DCE=30°,请你找出一个条件,使线段DE、AD、EB能构成一个等腰三角形,并求出此时等腰三角形顶角的度数;
(3)在(1)的条件下,如果AB=10,求BD?AE的值.