2008-2009学年度潍坊市奎文区第一学期九年级期中考试
数学试卷
时间:120分钟 120分
一、选择题(共10个小题,每小题3分,共30分)
1.下列关于 的方程中,一定是一元二次方程的是( )
的方程中,一定是一元二次方程的是( )
A.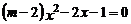 B.
B.
C.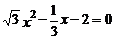 D.
D.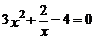
2.下列二次根式中,与 是同类二次根式的是( )
是同类二次根式的是( )
A.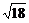 B.
B.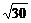 C.
C.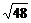 D.
D.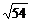
3.用配方法解方程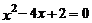 ,下列配方正确的是( )
,下列配方正确的是( )
A.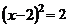 B.
B.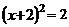 C.
C.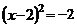 D.
D.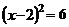
4.下列关于 的一元二次方程中,有两个不相等的实数根的方程是( ).
的一元二次方程中,有两个不相等的实数根的方程是( ).
A.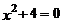 B.
B.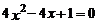
C.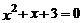 D.
D.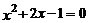
5.将抛物线 向上平移2个单位,得到抛物线的解析式是( ).
向上平移2个单位,得到抛物线的解析式是( ).
A.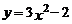 B.
B. C.
C.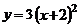 D.
D.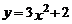
6.若 ,则
,则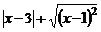 的值为( ).
的值为( ).
A.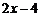 B.
B.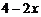 D.2
D.2
7.若抛物线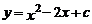 与
与 轴的交点为(0,-3),则下列说法不正确的是( )
轴的交点为(0,-3),则下列说法不正确的是( )
A.抛物线开口向上
B.抛物线的对称轴是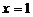
C.当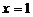 时,
时, 的最大值为-4
的最大值为-4
D.抛物线与 轴的交点为(-1,0),(3,0)
轴的交点为(-1,0),(3,0)
8.烟花厂设计制作了一种新型礼炮,这种礼炮的升空高度 (m)与飞行时间
(m)与飞行时间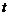 (s)的关系式是
(s)的关系式是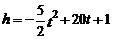 ,若这种礼炮在点火升空到最高点处引爆,则从点火升空到引爆需要的时间为( ).
,若这种礼炮在点火升空到最高点处引爆,则从点火升空到引爆需要的时间为( ).
A.3s B.4s C.5s D.6s
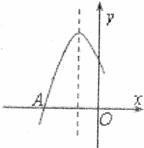
9.抛物线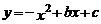 的部分图象如图所示,若
的部分图象如图所示,若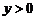 ,则
,则 的取值范围是( ).
的取值范围是( ).
A.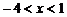 B.
B.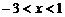 C.
C.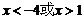 D.
D.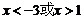

10.如下图是二次函数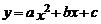 图象的一部分,图象过点A(-3,0),对称轴为
图象的一部分,图象过点A(-3,0),对称轴为 .给出四个结论:①
.给出四个结论:①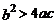 ;②
;②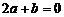 ;③
;③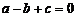 ;④
;④ .其中正确结论是( ).
.其中正确结论是( ).
A.②④ B.①④ C.②③ D.①③
二、填空题(共10个小题,每小题3分,共30分)
11.当 __________时,二次根式
__________时,二次根式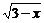 有意义.
有意义.
12.化简: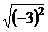 =__________.
=__________.
13.关于 的一元二次方程
的一元二次方程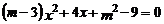 有一个根为0,
有一个根为0, 的值为__________.
的值为__________.
14.抛物线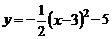 的对称轴是__________.
的对称轴是__________.
15.关于 的一元二次方程
的一元二次方程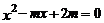 的一个根为1,则方程的另一根为__________.
的一个根为1,则方程的另一根为__________.
16.一元二次方程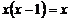 的解是__________.
的解是__________.
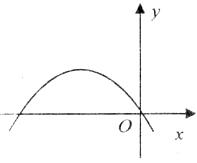
17.如下图所示的抛物线是二次函数 的图象,那么
的图象,那么 的值是__________.
的值是__________.
18.抛物线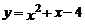 与
与 轴的交点坐标为__________.
轴的交点坐标为__________.
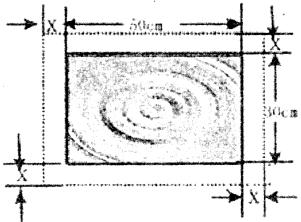
19.如图,在一幅长50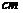 ,宽30
,宽30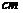 的风景画的四周镶一条金色纸边,制成一幅矩形挂图,如果要使整个矩形挂图的面积是1800
的风景画的四周镶一条金色纸边,制成一幅矩形挂图,如果要使整个矩形挂图的面积是1800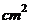 ,设金色纸边的宽为
,设金色纸边的宽为
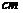 ,那么
,那么 满足的方程为__________.
满足的方程为__________.
20.如下图,小明的父亲在相距2米的两棵树间拴了一根绳子,给他做了一个简易的秋千,拴绳子的地方距地面高都是2.5米,绳子自然下垂呈抛物线状,身高1米的小明距较近的那棵树0.5米时,头部刚好接触到绳子,则绳子的最低点距地面的距离为__________米.

三、解答题(本题8个小题,共60分)
21.计算:(每小题3分,共6分)
(1)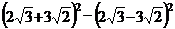
(2)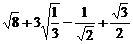
22.解方程:(每小题3分,共6分)
(1)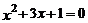
(2)用配方法解方程: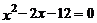
23.(6分)已知关于 的一元二次方程
的一元二次方程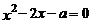 .
.
(1)如果此方程有两个不相等的实数根,求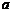 的取值范围;
的取值范围;
(2)如果此方程的两个实数根为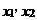 ,且满足
,且满足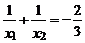 ,求
,求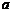 的值.
的值.
24.(8分)已知抛物线与 轴的交点是A(-2,0)、B(1,0),且经过点C(2,8)
.
轴的交点是A(-2,0)、B(1,0),且经过点C(2,8)
.
(1)求该抛物线的解析式;
(2)求该抛物线的顶点坐标.
25.(8分)汽车产业的发展,有效促进我国现代化建设.某汽车销售公司2005年盈利1500万元,到2007年盈利2160万元,且从2005年到2007年,每年盈利的年增长率相同.
(1)该公司2006年盈利多少万元?(6分)
(2)若该公司盈利的年增长率继续保持不变,预计2008年盈利多少万元?(2分)
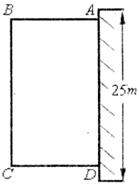
26.(8分)为了改善小区环境,某小区决定要在一块一边靠墙(墙长25 )的空地上修建一个矩形绿化带ABCD,绿化带一边靠墙,另三边用总长为40
)的空地上修建一个矩形绿化带ABCD,绿化带一边靠墙,另三边用总长为40 的栅栏围住(如下图).若设绿化带的BC边长为
的栅栏围住(如下图).若设绿化带的BC边长为
 ,绿化带的面积为
,绿化带的面积为
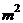 .
.
(1)求 与
与 之间的函数关系式,并写出自变量
之间的函数关系式,并写出自变量 的取值范围;
的取值范围;
(2)当 为何值时,满足条件的绿化带的面积最大?
为何值时,满足条件的绿化带的面积最大?
27.(9分)如图,隧道的截面由抛物线AED和矩形ABCD构成,矩形的长BC为8 ,宽AB为2
,宽AB为2 ,以BC所在的直线为
,以BC所在的直线为 轴,线段BC的中垂线为
轴,线段BC的中垂线为 轴,建立平面直角坐标系,
轴,建立平面直角坐标系, 轴是抛物线的对称轴,顶点E到坐标原点O的距离为6
轴是抛物线的对称轴,顶点E到坐标原点O的距离为6 .
.
(1)求抛物线的解析式;
(2)一辆货运卡车高4.5 ,宽2.4
,宽2.4 ,它能通过该隧道吗?
,它能通过该隧道吗?
(3)如果该隧道内设双行道,为了安全起见,在隧道正中间设有0.4 的隔离带,则该辆货运卡车还能通过隧道吗?
的隔离带,则该辆货运卡车还能通过隧道吗?

28.(9分)某水果批发商销售每箱进价为40元的苹果,物价部门规定每箱售价不得高于55元,市场调查发现,若每箱以50元的价格售出,平均每天销售90箱,价格每提高1元,平均每天少销售3箱.
(1)求平均每天销售最 (箱)与销售价
(箱)与销售价 (元/箱)之间的函数关系式.
(元/箱)之间的函数关系式.
(2)求该批发商平均每天的销售利润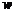 (元)与销售价
(元)与销售价 (元/箱)之间的函数关系式.
(元/箱)之间的函数关系式.
(3)当每箱苹果的销售价为多少元时,可以获得最大利润?最大利润是多少?