2008年滨城区联考数学试卷
一、选择题
1．若关于
的方程
的两根均为正数，则点
在第（
）象限。
A．一 B．二 C．三 D． 四
2．半径为7的圆，其圆心在坐标原点，则下列各点在圆外的是：（ ）
A．（3，4） B．（4，4） C．（4，5） D．（4，6）
3．期中考试后，班长算出了全班40个人数学成绩的平均分为M，如果把M当成一个同学的分数，与原来的40个分数一起，算出这41个分数的平均值为N，那么M∶N为（ ）
A．40／41 B．
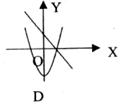
4．在同一直角坐标系中，一次函数与二次函数的图像大致为（ ）
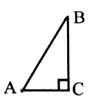
5．已知Rt△ABC的斜边AB=
A．65
B． C．156 D．300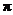
6．AB是⊙
的直径，弦CD垂直平分OB，则∠BDA的度数为（ ）
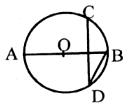
A．20º B．15º C．30º D．45º
7．若点P（a，b）在第四象限，则P点到X轴的距离为：
A．-a B．a C．b D．-b
8．某一元二次方程的两实根为
，
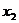，如果一根比3大，另一根比3小，则下列结论正确的是：（ ）
A．
B．
C． 
D．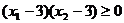
9．在一个圆形博物馆的墙壁安装电子监视仪，使博物馆室内每一个角落都能监视到，若每只监视仪最大监视角为30º，则至少要安装监视仪的个数为（ ）
A．12 B．8 C．6 D．4
10．小李在假期中记录了他钓鱼的小时数和他累计钓到鱼的条数，如下表所示：
小时数：
l
3
5
8
10
条数：
4
8
12
18
22
则可以描述钓鱼的时问和钓到鱼的条数之间的关系是：（ ）
A．
B．
C．
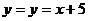D．
二、填空
11．老师给出一个函数，甲、乙、丙分别正确指出了这个函数的一个性质：
甲：函数的图像经过第一象限； 乙：函数的图像经过第二象限：
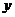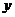丙：在第一象限内，随的增大而增大；在第二象限内，随的增大而减小；
请你根据他们的叙述构造满足上述性质的一个函数： 。
12．某石英钟表盘上有一没有显现的平面直角坐标系，当时钟为9：00和9：15时，分针针尖的坐标分别为（0，2）和（2，0），则当时钟为9：45时，分针针尖所在点的坐标为 。
13．某年运动会射击项目选拔赛，四人的平均成绩和方差如下表所示，则在四人中选拔的最佳人选为 。
甲
乙
丙
丁
平均环数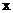
8.5
8.8
8.8
8
方差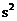
3.5
3.5
2.1
8.7
14．近视眼镜的度数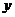（度）与镜片焦距（米）成反比例，已知200度近视眼镜片的焦距为0.5米，则眼镜度数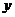与镜片焦距之间的函数关系式为 。
15．一组数据5，7，7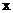，的中位数与平均数相等，则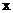的值为 。
16．两圆半径之比为4∶3，它们相内切时，圆心距为2cm，那么它们相外切时圆心距为 cm。
17．在⊙中，弦AB=1.8cm，圆周角∠ACB=30º，则⊙的直径等于 cm。
18．A、B是圆上两点，且∠AOB=70º，C是圆上不与A，B重合的任意一点，则∠ACB的度数是 。
19．如果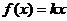
，
，那么
= 。
20．已知圆锥的底面半径为2cm，母线长为6cm，则圆锥的侧面展开图的圆心角为 度。
三、证明与计算
21．为了加强市区交通秩序管理，交警部门在十字路口安装了红绿灯实行交通管制，以下数据是某十字路口处十个相同时间段（即绿灯亮一次的持续时间，红绿灯间隔40秒）内南北方向机动车辆通过的数据：
15、22、15、17、18、15、1 9、15、20、14
（1）填空：这组数据的众数是 ，中位数是 。
（2）通过计算后，请你估计1小时内南北方向通过该路口的车辆有多少?
22．在防治“禽流感”的战役中，为防止疫情扩散，某制药厂接到了生产240箱疫苗的任务，在生产了60箱后，因为任务紧急，需要加快生产，每天比原来多生产l5箱，结果6天就完成了任务，求加快速度后每天生产多少箱疫苗。
（1）货轮从A港口出发以后直到B港口与巡逻艇一共相遇了几次？
（2）出发多长时间巡逻艇与货轮第三次相遇？此时离A港口多少千米？
24．已知半径为
和
的两圆相交，公共弦长为，则两圆的圆心距为多少？
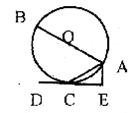
25．AB是⊙的直径，DE切⊙于点C，欲使AE⊥DE，须添加的一个条件是什么？（不另外添加线和点，至少写出两种）
26、已知一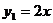次函数
，二次函数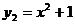
，
（1）根据表中给出的的值，计算对应的函数值
，
，并填在表格中：
-3
-2
-1
0
1
2
3
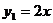
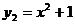
（2）观察第（1）问表中有关数据，证明如下结论：在实数范围内，对于的同一个值，这两个函数所对应的函数值
均成立；
（3）试问，是否存在二次函数
，其图像经过点（-5，2），且在实数范围内，对于的同一个值，这三个函数所对应的函数值
均成立，若存在，求出函数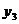
的解析式：若不存在，请说明理由。