2008年从化市初中毕业生综合测试
数学试卷
本试卷分选择题和非选择题两部分,共三大题25小题,满分150分.考试时间120分钟.
第一部分 选择题 (共30分)
一、选择题(本大题共10小题,每小题3分,共30分. 在每小题给出的四个选项中,只有一项是符合题目要求的)
1、a是3的倒数,那么a的值等于( )
A.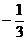 B.-3 C.3
D.
B.-3 C.3
D. 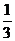
2、下列图形中,既是轴对称图形又是中心对称图形的是 ( )

3、下列运算正确的是( )
A、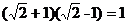 B、
B、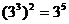
C、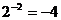 D、
D、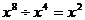
4、下列函数中,图象经过点(-1,2)的反比例函数解析式是( )
A、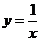 B、
B、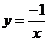 C、
C、 D、
D、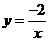
5、下列一元二次方程中,有两个不相等的实数根的是( )
A、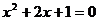 B、
B、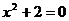
C、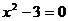 D、
D、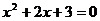
6、如图,已知△ABC为直角三角形,∠C=90°,若沿图中虚线剪去∠C,则∠1+∠2等于 ( )
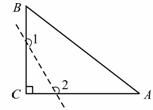
A、315° B、 270° C、135° D、 90°
7、如果两圆半径分别为3和4,圆心距为6,那么这两圆的位置关系是( )
A、相交 B、内切 C、外离 D、外切
8、已知一次函数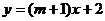 的图象如图所示,那么m的取值范围是( )
的图象如图所示,那么m的取值范围是( )
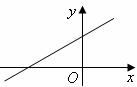
A、m<
9、如图,小王同学从A地沿北偏西60º方向走100m到B地,再从B地向正南方向走200m到C地,此时小王同学距离A地 ( )
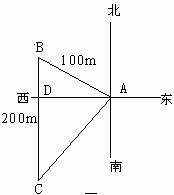
A、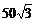 m B、100 m C、
m B、100 m C、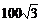 m D、150m
m D、150m
10、如图,这是中央电视台“曲苑杂谈”中的一副图案,它是一扇形图形,其中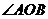 为
为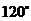 ,
,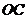 长为8cm,
长为8cm,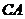 长为12cm,则阴影部分的面积为( )
长为12cm,则阴影部分的面积为( )

A、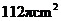 B、
B、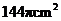 C、
C、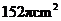 D、
D、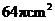
第二部分 非选择题 (共120分)
二、填空题(本大题共6题,每题3分,满分18分)
11、随着中国综合国力的提升,近年来全球学习汉语的人数不断增加.据报道,2005年海外学习汉语的学生人数已达38200 000人,用科学记数法表示为 人;
12、要使二次根式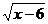 有意义,
有意义, 应满足的条件是
.
应满足的条件是
.
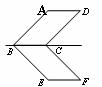
13、如图,若□ABCD与□EBCF关于BC所在直线对称,∠ABE=90°,则∠F的 度数为 。
14、不等式组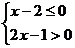 的整数解的和是_____ _____。
的整数解的和是_____ _____。
15、如图,为了测量学校旗杆的高度,小东用长为3.2m的竹竿做测量工具。移动竹竿、旗杆顶端的影子恰好落在地面的同一点,此时,竹竿与这一点相距8m,与旗杆相距22m,则旗杆的高为_____ _____m。

16、已知二次函数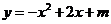 的部分图象如图所示,则关于
的部分图象如图所示,则关于 的一元二次方程
的一元二次方程
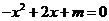 的解为
.
的解为
.
三、解答题(本大题共9小题,共102 分.解答应写出文字说明、证明过程或演算步骤)
17、(本小题满分9分)
解方程:
18、(本小题满分9分)
如图,矩形PMON的边OM,ON分别在坐标轴上,且点P的坐标为(-2,3)。将矩形PMON向右平移4个单位,得到矩形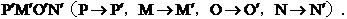

(1)请在上图的直角坐标系中画出平移后的矩形;
(2)求直线OP的函数解析式.
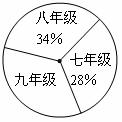
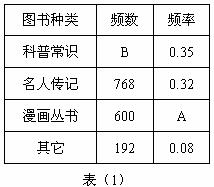
(1)求该校九年级的人数占全校总人数的百分率.
(2)求出表(1)中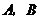 的值.
的值.
(3)该校学生平均每人读多少本课外书?
20、(本小题满分10分)
一个盒子中装有四张完全相同的卡片,分别写着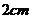 ,
,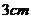 ,
,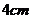 和
和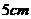 ,盒子外有两张卡片,分别写着
,盒子外有两张卡片,分别写着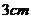 和
和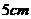 .现随机从盒内取出一张卡片,与盒子外的两张卡片放在一起,以卡片上的数量分别作为三条线段的长度,解答下列问题:
.现随机从盒内取出一张卡片,与盒子外的两张卡片放在一起,以卡片上的数量分别作为三条线段的长度,解答下列问题:
(1)求这三条线段能构成三角形的概率;
(2)求这三条线段能构成等腰三角形的概率.
21、(本小题满分12分)
如图,AB切⊙O于点B,OA交⊙O于C点,过C作DC⊥OA交AB于D,
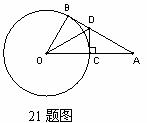
(1)求证:△COD≌△B0D;
(2)若∠A =32°,AD=8, 求⊙O的半径(精确到0.01cm)
22、(本小题满分12分)
团体购买公园门票票价如下:
购票人数
1~50
51~100
100人以上
每人门票(元)
13元
11元
9元
今有甲、乙两个旅行团,已知甲团人数少于50人,乙团人数不超过100人。若分别购票,两团共计应付门票费1392元,若合在一起作为一个团体购票,总计应付门票费1080元.
(1) 乙团的人数是否也少于50人?为什么?
(2) 甲、乙两旅行团各有多少人?
23、(本小题满分12分)
二次函数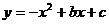 的图象如图所示,解答下列问题:
的图象如图所示,解答下列问题:

(1)根据图象写出 随
随 的增大而增大的自变量
的增大而增大的自变量 的取值范围.
的取值范围.
(2)求b,c的值.
(3)若方程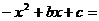 k有实数根,求实数
k有实数根,求实数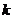 的取值范围.
的取值范围.
24、(本小题满分12分)
如图,在直角坐标系中放入一边长OC为6的矩形纸片ABCO,将纸翻折后,使点B恰好落在x轴上,记为B′,折痕为CE,已知tan∠OB′C=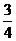 .
.
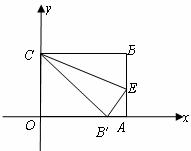
(1)求出B′点的坐标;
(2)求折痕CE所在直线的解析式。
25、(本小题满分14分)
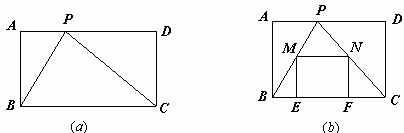
如图(a),已知:在矩形ABCD中,AB=6,点P在AD边上.
(1)如果∠BPC=90°,求证:△ABP∽△DPC;
(2)在(1)中,当AD =13时,求tan∠PBC;
(3)如图(b),原题目中的条件不变,且AP =3,DP =9,M是线段BP上一点,过点M作MN∥BC交PC于点N,分别过点M、N作ME⊥BC于点E,NF⊥BC于点F,并且矩形MEFN和矩形ABCD的长与宽之比相等,求MN.