2007-2008学年度烟台市招远第二学期初三期末考试
数学试卷
说明:
1.本试卷试题共115分;
2.书写质量3分;
3.卷面安排2分;
整个试卷满分为120分。
一、选择题:(每小题2分,满分30分)
1.反比例函数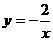 的图像位于
的图像位于
A.第一、二象限内 B.第一、三象限内
C.第二、三象限内 D.第二、四象限内
2.若关于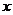 的方程
的方程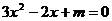 的一个根是-1,则
的一个根是-1,则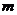 的值为
的值为
A.-5 B.-1 C.1 D.5
3.下列条件中不能确定四边形ABCD是平行四边形的是
A.AB=CD,AD∥BC B.AB=CD,AB∥CD
C.AB∥CD,AD∥BC D.AB=CD,AD=BC
4.如下图,△ABC中,∠C=90°,∠B=45°,AD是角平分线,DE⊥AB于E,则下列结论不正确的是

A.AC=AE B.CD=DE C.CD=DB D.AB=AC+CD
5.对某班60名同学的一次数学测验成绩进行统计,如果频数分布直方图中80.5~90.5分这一组的频数是18,那么这个班的学生这次数学测验成绩在80.5~90.5分之间的频率是
A.18 B.0.4 C.0.3 D.0.35
6.已知一个矩形的两条对角线夹角为60°,一条对角线的长为
A.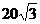 cm2
cm2
C. cm2 D.
cm2 D.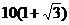 cm2
cm2
7.如果反比例函数 的图像具有下列特征:在所在的象限内,
的图像具有下列特征:在所在的象限内,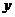 的值随
的值随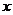 值的增大而减小,那么
值的增大而减小,那么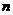 的取值范围是
的取值范围是
A.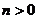 B.
B.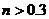 C.
C.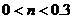 D.
D.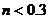
8.如下图,点D、E分别在等边三角形ABC的边BC、AC上,且BD=CE,连接AD、BE相交于点P,则∠APE的度数是
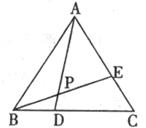
A.60° B.55° C.45° D.30°
9.若关于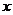 的方程
的方程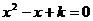 没有实数根,则
没有实数根,则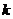 的取值范围是
的取值范围是
A.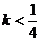 B.
B.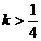 C.
C. D.
D.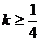
10.在一个不透明的口袋中,有大小、形状完全相同,颜色不同的球15个,从中任摸出一球,若摸到红球的概率为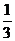 ,则袋中红球的个数为
,则袋中红球的个数为
A.15 B.
11.如下图,在菱形ABCD中,AE⊥BC于点E,AF⊥CD于点F,E,F分别为BC、CD的中点,则∠EAF等于
A.75° B.60° C.45° D.30°
D.它的图像位于第二、四象限内,且在每一个象限内, 的值随
的值随 值的增大而增大
值的增大而增大
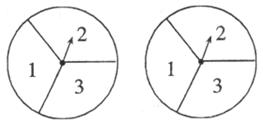
13.小刚与小亮一起玩一种转盘游戏。如下图是两个完全相同的转盘,两个转盘都被分成面积相等的三个扇形,分别用“1”、“2”、“3”表示,固定指针,同时转动两个转盘,任其自由停止(假定每次都能确定指针所指的数字),若两指针指的数字均为奇数,则小刚获胜;否则小亮获胜,则在该游戏中小刚获胜的概率是
A.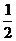 B.
B.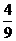 C.
C.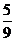 D.
D.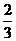
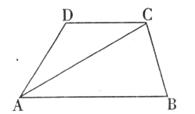
14.如下图,等腰梯形ABCD中,AB∥CD,AC⊥BC,且AC平分∠BAD,若梯形的中位线长为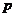 ,则梯形ABCD的周长为
,则梯形ABCD的周长为
A.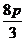 B.
B. C.
C.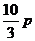 D.
D.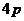
15.若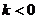 ,则反比例函数
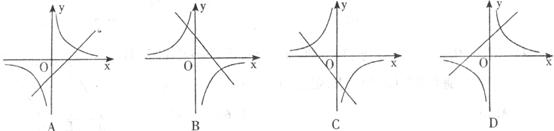
,则反比例函数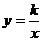 和一次函数
和一次函数 的图像大致是
的图像大致是
二、填空题:(将正确答案填在横线上,每小题3分,满分30分)
16.若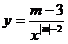 是反比例函数,则
是反比例函数,则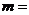
17.请写出一个一元二次方程,使其有两个不相等的正数根,你所写的方程是
18.如下图,在□ABCD中,E为CD上一点,DE┱CE=2┱3,连接AE、BE、BD,且AE、BD交于点F,则S△DEF┱S△EBF┱S△ABF=
19.底角为15°,腰长为2的等腰三角形的面积是
20.将一枚均匀的硬币连掷三次,则出现2次正面朝上、1次反面朝上的概率是
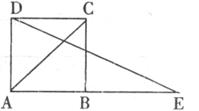
21.如下图,延长正方形ABCD的AB边至点E,使BE=AC,则∠BED= 度。
22.已知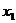 ,
,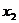 是方程
是方程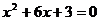 的两实数根,则
的两实数根,则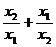 的值为
的值为
23.考察函数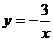 的图像,当
的图像,当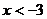 时,y的取值范围是
时,y的取值范围是
24.一个不透明的袋子里装有除颜色外完全相同的2个红球和2个黄球,从袋中任意摸出一个球,然后放回袋中,再任意摸出一个球,则两次摸到的球是一红一黄的概率是
25.如下图,等腰梯形ABCD中,AB∥CD,AB=
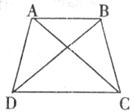
三、解答题:(每题8分,满分16分)
26.已知反比例函数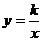 和一次函数
和一次函数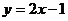 ,其中一次函数的图像经过点(
,其中一次函数的图像经过点(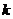 ,5)。
,5)。
(1)求反比例函数的表达式;
(2)求两函数的图像的交点A的坐标。
27.如下图,□ABCD的对角线相交于点O,且AC⊥AB,OC=
求AB的长及□ABCD的面积。

四、实际应用题:(28题9分,29题10分,满分19分)
28.某工程队接受一项开挖水渠的工程,所需天数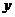 (天)与每天完成的工程量
(天)与每天完成的工程量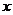 (m/天)的函数关系图像如下图所示。
(m/天)的函数关系图像如下图所示。
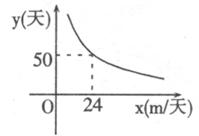
(1)共需开挖水渠多少米?
(2)求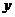 与
与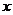 之间的函数表达式;
之间的函数表达式;
(3)如果为了防汛工作的紧急需要,必须在一个月内(按30天计算)完成任务,那么每天至少要完成多少米?
29.如下图,四张卡片(形状、大小和质地都相同),正面上分别写有字母A、B、C、D和一个算式。将这四张卡片反面向上洗匀,从中随机抽取一张,记录字母后放回(反面向上),重新洗匀后再从中随机抽取一张,记录字母。请用列表的方法求抽取的两张卡片上算式都正确的概率和只有一个算式正确的概率。

五、探索题:(每题10分,满分20分)
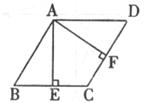
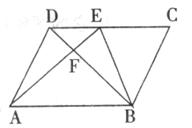
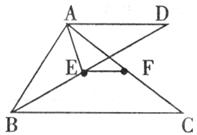
30.如下图,点F是△ABC的AC边中点,过点A作BC的平行线,与∠ABC的平分线相交于点D,E为BD的中点。
试探究:(1)AE与BD的位置关系,并给予证明;
(2)EF、AB、BC之间的数量关系,并给予证明。
31.如下图,正方形ABCD中,G是CD边上的一个动点(点G与C、D不重合),以CG为一边向正方形ABCD外作正方形GCEF,连接DE,连接BG并延长交DE于H。
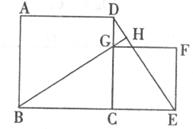
(1)求证:∠BGC=∠DEC。
(2)若正方形ABCD的边长为1,试问当点G运动到什么位置时,BH垂直平分DE?