2007-2008学年度淄博市张店区第二学期初三年级期末考试
数学试卷
一、选择题(在每小题给出的四个选项中,只有一个是正确的)
1、下列说法正确的是
A.“明天降雨的概率是80%”表示明天有80%的时间降雨
B.“抛一枚硬币正面朝上的概率是
C.“彩票中奖的概率是1%”表示买100张彩票一定会中奖
D.“抛一枚正方体骰子朝正面的数为奇数的概率是
2、方程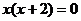 的根是
的根是
A.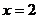 B.
B.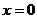
C.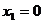 ,
,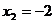 D.
D.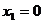 ,
,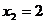
3、在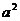 □
□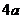 □4空格□中,任意填上“+”或“-”,在所得到的代数式中,能构成完全平方式的概率是
□4空格□中,任意填上“+”或“-”,在所得到的代数式中,能构成完全平方式的概率是
A.1 B.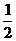 C.
C.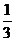 D.
D.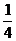
4、甲、乙、丙三个同学排成一排拍照,则甲排在中间的概率是
A.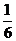 B.
B.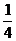 C.
C.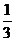 D.
D.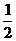
5.将一正方形纸片按下列顺序折叠,然后将最后折叠的纸片沿虚线剪去上方的小三角形
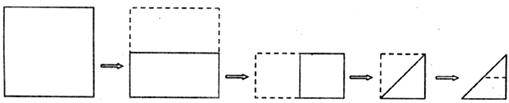
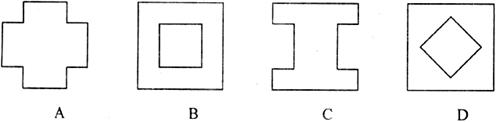
将纸片展开,得到的图形是
6.若关于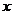 的一元二次方程
的一元二次方程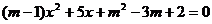 的常数项为0,则
的常数项为0,则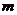 的值等于
的值等于
A.1 B.2 C.1或2 D.0
7.如下左图,在矩形ABCD中,动点P从点B出发,沿BC,CD,DA运动至点A停止。设点P运动的路程为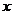 ,△ABP的面积为
,△ABP的面积为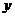 ,如果
,如果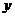 关于
关于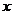 的函数图像如下右图所示,则△ABC的面积是
的函数图像如下右图所示,则△ABC的面积是
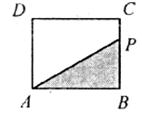
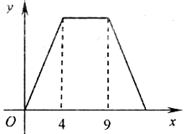
A.10 B.16 C.18 D.20
8、已知点(-2,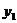 ),(-1,
),(-1, ),(3,
),(3,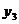 ),和(-3,-2)都在反比例函数
),和(-3,-2)都在反比例函数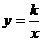 的图像上,那么
的图像上,那么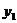 ,
, 与
与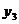 的大小关系是
的大小关系是
A.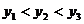 B.
B. C.
C.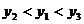 D.
D.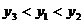
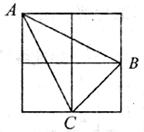
9、如下左图,由四个小正方形组成的田字格中,△ABC的顶点都是小正方形的顶点。在田字格上画与△ABC成轴对称的三角形,且顶点都是小正方形的顶点,则这样的三角形(不包含△ABC本身)共有
A.1个 B.2个 C.3个 D.4个
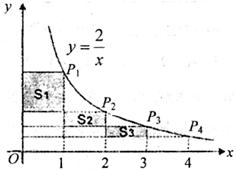
10、如上右图,在反比例函数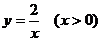 的图像上,有点
的图像上,有点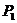 ,
,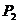 ,
,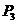 ,
,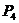 ,它们的横坐标依次为1,2,3,4。分别过这些点作
,它们的横坐标依次为1,2,3,4。分别过这些点作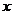 轴与
轴与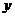 轴的垂线,图中所构成的阴影部分的面积从左到右依次为
轴的垂线,图中所构成的阴影部分的面积从左到右依次为 ,
,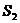 ,
,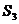 ,则
,则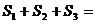
A.1 B.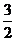 D.4
D.4
二、填空题
1、对于平面内任意一个凸四边形ABCD,现从以下四个关系式①AB=CD;②AD=BC;③AB∥CD;④∠A=∠C中任取两个作为条件,能够得出这个四边形ABCD是平行四边形的概率是
2、“上升数”是一个数中右边数字比左边数字大的自然数(如:34,568,2469等)。任取一个两位数,是“上升数”的概率是
3.如下图,C为线段AE上一动点(不与点A,E重合),在AE同侧分别作正三角形ABC和正三角形CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连结PQ。以下五个结论:
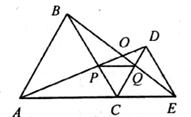
①AD=BE; ②PQ∥AE; ③AP=BQ; ④DE=DP; ⑤∠AOB=60°
恒成立的有 (把你认为正确的序号都填上)
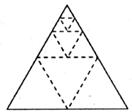
4、将一个正三角形纸片剪成四个全等的小正三角形(如下图),再将其中的一个按同样的方法剪成四个更小的正三角形,……如此继续下去,结果如下表
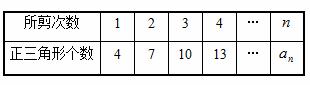
则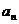 = (用含
= (用含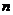 的代数式表示)
的代数式表示)
5、在-9,-6,-3,-1,2,3,6,8,11这九个数中,任取一个作为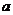 值,能够使关于
值,能够使关于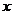 的一元二次方程
的一元二次方程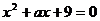 有两个不相等的实数根的概率是
有两个不相等的实数根的概率是
6、根据图中数字的规律,在最后一个图形中填空。

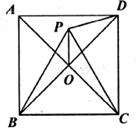
7、如图所示,正方形ABCD的对角线交于O,△PBC是等边三角形,△PBO的面积为1,则△BPD的面积是
8、如图,当四边形PABN的周长最小时,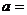
三、解答题
1、“一方有难,八方支援”,四川汶川大地震牵动着全国人民的心,我市某医院准备从甲、乙、丙三位医生和A、B两名护士中选取一位医生和一名护士支援汶川。
(1)若随机选一位医生和一名护士,用树状图(或列表法)表示所有可能出现的结果;
(2)求恰好选中医生甲和护士A的概率。
2、某活动小组为了估计装有5个白球和若干个红球(每个球除颜色外都相同)的袋中红球接近多少个,在不将袋中球倒出来的情况下,分小组进行摸球试验,两人一组,共20组进行摸球实验。其中一位学生摸球,另一位学生记录所摸球的颜色,并将球放回袋中摇匀,每一组做400次试验,汇总起来后,摸到红球次数为6000次。
(1)估计从袋中任意摸出一个球,恰好是红球的概率是多少?
(2)请你估计袋中红球接近多少个?
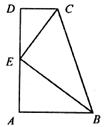
3、如图,在梯形ABCD中,AB∥CD,∠A=90°,AB=2,BC=3,CD=1,E是AD中点。
求证:CE⊥BE。
4、(1)探究新知:
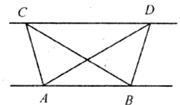
如图,已知△ABC与△ABD的面积相等,试判断AB与CD的位置关系,并说明理由。
(2)结论应用:
①如下左图,点M、N在反比例函数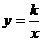
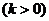 的图像上,过点M作ME⊥
的图像上,过点M作ME⊥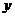 轴,过点N作NF⊥
轴,过点N作NF⊥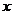 轴,垂足分别为E,F。试证明:MN∥EF。
轴,垂足分别为E,F。试证明:MN∥EF。
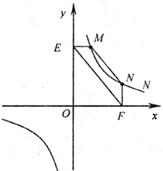
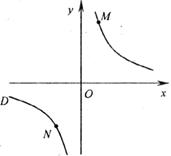
②若①中的其他条件不变,只改变点M,N的位置如上右图所示,请判断MN与EF是否平行。
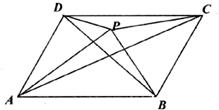
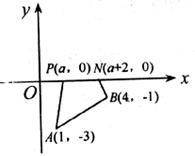
5、如下图,点P是平行四边形ABCD内一点,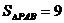 ,
,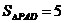 ,求三角形PAC的面积。
,求三角形PAC的面积。