2007-2008学年度济宁市嘉祥县第二学期九年级期中考试
数学试卷
卷Ⅰ(选择题,共36分)
一、选择题(本大题共l2个小题;每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.计算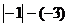 的值是
的值是
A. 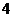 B.
B. 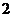 C.
C.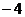 D.
D.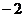
2.通过四舍五入得到的近似值3.56万精确到
A.万位 B.千位 C.百位 D.百分位
3.如图是某一几何体的三视图.则该基本几何体为
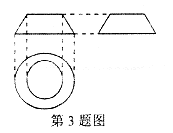
A.圆锥 B.圆柱 C.圆台 D.棱台
4.计算 的结果是
的结果是
A.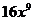 B.
B. C.
C. D.
D.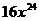
5.如图,将正方形图案绕中心O旋转180º后,得到的图案是
6.为了改善住房条件,小亮的父母考察了某小区的A、B两套楼房,A套楼房在第3层楼,B套楼房在第5层楼,B套楼房的面积比A套楼房的面积大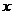 平方米,B套楼房的面积为
平方米,B套楼房的面积为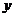 平方米,根据以上信息得出了下列方程组,其中正确的是
平方米,根据以上信息得出了下列方程组,其中正确的是
A.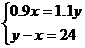 B.
B.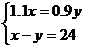
C.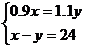 D.
D. 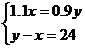
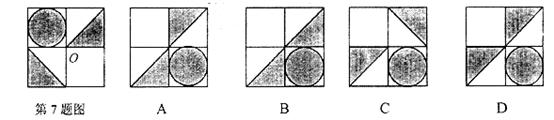
7.同学们还记得“乌鸦喝水”的故事吧,在一片树林里有一只丢弃的圆柱形玻璃瓶中盛了一点水,由于瓶口直径Dcm较小,水又比较少,只有hcm高,而瓶高有Hcm(H>h)乌鸦根本喝不到水,乌鸦想到了往玻璃瓶中叼碎石子使水面上升的办法,那么乌鸦需叼多少cm3的碎石子才能喝到水(与瓶口持平)义不至于溢出来?
A. B.
B. 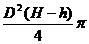
C. D.
D.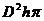
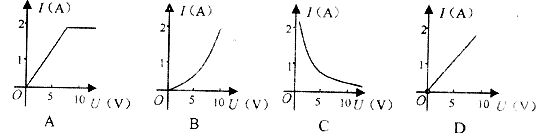
8.如果一定值电阻R两端所加电压为5V时,通过它的电流为
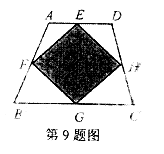
9.如图,是一个风筝的平面示意图,四边形ABCD是等腰梯形,E、F、G、H分别是各边的中点.假设图中阴影部分所需布料的面积为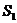 ,其它部分所需布料的面积之和为
,其它部分所需布料的面积之和为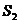 (边缘外的布料不计).则
(边缘外的布料不计).则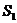 与
与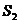 的大小关系为
的大小关系为
A.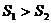 B.
B.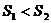
C.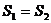 D.不确定
D.不确定
10.三角形一边长为10.另两边K是方程 的两实根,则这是一个()三角形.
的两实根,则这是一个()三角形.
A.直角三角形 B.锐角三角形
C.钝角二角形 D.等腰三角形
11.某学习小组5位同学参加初中毕业生实验操作考试(满分20分)的平均成绩是l6分,其中三位男生的方差为6(分2),两位女生的成绩分别为17分,15分.则这个学习小组5位同学考试分数的标准差为
A. B.2 C.
B.2 C.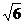 D 6
D 6
12.任何一个正整数n都可以进行这样的分解: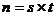 (s,t是正整数,且s≤t),
(s,t是正整数,且s≤t),
如果 在n的所有这种分解中两因数之差的绝对值最小,我们就称
在n的所有这种分解中两因数之差的绝对值最小,我们就称 是n的最佳分解,并规定:
是n的最佳分解,并规定: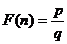 .例如18可以分解成l×18,2×9,3×6这三种,这时就有
.例如18可以分解成l×18,2×9,3×6这三种,这时就有 .给出下列关于
.给出下列关于 的说法:(1)
的说法:(1)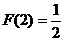 (2)
(2)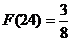 (3)
(3)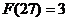 (4)若
(4)若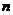 是一个完全平方数,则
是一个完全平方数,则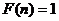 .其中正确说法的个数是
.其中正确说法的个数是
A.1 B.2 C.3 D.4
卷Ⅱ(非选择题 共84分)
二、填空题(本大题共6个小题;每小题3分,共18分.把答案写在题中横线上)
13、一个长方形的面积是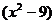 平方米,其长为
平方米,其长为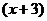 米用含有
米用含有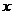 的整式表示它的宽为 米。
的整式表示它的宽为 米。
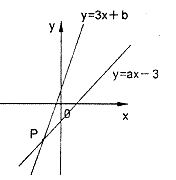
14、如图,己知函数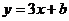 和
和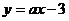 的图像交于点P(-2,-5),则根据图像可得不等式
的图像交于点P(-2,-5),则根据图像可得不等式 的解集是
的解集是
15.已知在正方形网格中,每个小方格都是边长为1的正方形,A、B两点在小方格的顶点上,位置如幽所示,点C也在小方格的顶点上,且以A、B、C为顶点的三角形的面积为1个平方单位,则点C的个数为 个 .

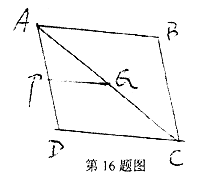
16.在菱形ABCD中,P、Q分别是AD、AC的中点,如果PQ=3,那么菱形ABCD的周长是 .
17.某商场在促销期间规定:商场内所有商品按标价的80%出售,同时,当顾客在该商场内消费满一定金额后,按如下方案获得相应金额的奖券.(奖券购物不再享受优惠)
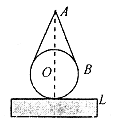
消费金额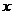 的范围(元)
的范围(元)
200≤x<400
400≤x<500
500≤x<700
获得奖券的金额(元)
30
60
100
根据上述促销方法,顾客在该商场购物可获得双重优惠,如果
18.用一个直径为l
三、解答题(本大题共9个小题;共66分)
19.(本小题满分7分)
先化简,再求值: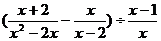 ,其中
,其中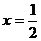
20.(本小题满分7分)
观察下面的点阵图,探究其中的规律.摆第1个“小屋子”需要5个点;摆第2个“小屋子”需要11个点:摆第3个“小屋子”需要17个点.
(1)摆第10个这样的“小屋子”需要多少个点?
(2)写出摆第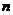 个这样的“小屋子”需要的总点数S与
个这样的“小屋子”需要的总点数S与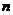 的关系式.
的关系式.

21.(本小题满分9分)
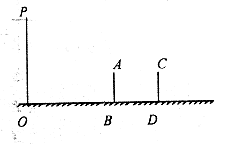
如图,是小亮晚上在广场散步的示意图,图中线段AB表示站立在广场上的小亮,线段PO表示直立在广场上的灯杆,点P表示照明灯的位置.
(1)在小亮由 B 处沿OB所在的方向行走的过程中,他在地面上的影子的变化情况为 :
(2)请你在图中画出小亮站在AB处的影子;
(3)当小亮离开灯杆的距离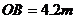 时, 身高(AB)为
时, 身高(AB)为
问当小亮离开灯杆的距离OD=
22.(本小题满分9分)
在物理试验中,当电流在一定时间段内正常通过电子元 电或断开,并且这两种状态的可能性相等.
电或断开,并且这两种状态的可能性相等.
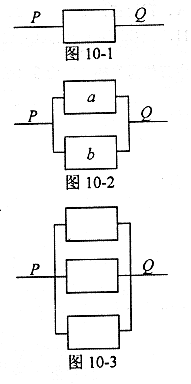
(1)如图10―1,当只有一个电子元件时,P,Q之间电流通过的概率是 .
(2)如图10―2,当有两个电子元件a,b并联时,请你用树状图(或列表法)表示图中P,Q之间电流能否通过的所有可能情况,求出P,Q之间电流通过的概率;
(3)如图10―3,当有三个电子元件并联时,请你猜想P,Q之间电流通过的概率是 .
23.(本小题满分10分)
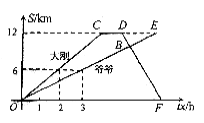
如图,表示的大刚与爷爷春游时,沿相同的路线同时从山脚下出发到达山顶的过程中,各自行进的路程随时间变化的图像.请你根据图像提供的信息解答下列问题:
(1)试写出在登山过程中,大刚行进的路程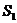 (km)与时间
(km)与时间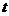 (h)之间的函数关系式为 ,爷爷行进的路程
(h)之间的函数关系式为 ,爷爷行进的路程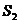 (km)与时间
(km)与时间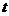 (h)之间的函数关系式为 ;(都不要求写出自变量
(h)之间的函数关系式为 ;(都不要求写出自变量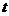 的取值范围)
的取值范围)
(2)当大刚到达山顶时,爷爷行进到山路上某点A处,求点A距山顶的距离:
(3)在(2)条件下,设爷爷从A处继续登山,大刚到达山顶后休息1h,沿原路下山,在点B处与爷爷相遇,此时点B与山顶的距离为
24.(本小题满分12分)
(1)已知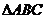 中,
中, ,
,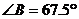 ,请画一条直线,把这个三角形分割成两个等腰三角形.(请你选用下面给出的备用图,把所有不同的分割方法都画出来.只需画图,不必说明理由,但要在图中标出相等两角的度数)
,请画一条直线,把这个三角形分割成两个等腰三角形.(请你选用下面给出的备用图,把所有不同的分割方法都画出来.只需画图,不必说明理由,但要在图中标出相等两角的度数)

(2)已知△ABC中,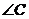 是其最小的内角,过顶点B的一条直线把这个三角形分割成了两个等腰三角形,请探求
是其最小的内角,过顶点B的一条直线把这个三角形分割成了两个等腰三角形,请探求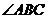 与
与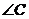 之间的关系.
之间的关系.
25.(本小题满分12分)
如图,点M(4,0),以点M为圆心、2为半径的圆与X轴交于点A、B.已知抛物线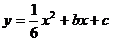 过点A和B,与y轴交于点C.
过点A和B,与y轴交于点C.
(1)求点C的坐标,并画出抛物线的大致图像。
(2)点Q(8,m)在抛物线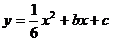 上,点P为此抛物线对称轴上一个动点,求
上,点P为此抛物线对称轴上一个动点,求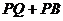 的最小值.
的最小值.
(3)CE是过点C的OM的切线,点E是切点, 求OE所在直线的解析式.
