2007-2008学年度德州乐陵第二学期八年级期末质量检测
数学试卷
第 I 卷(选择题,共24分)
一、选择题:你的数学风采,在于你的合理选择!
1、下列分式的运算正确的是( )
A、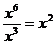 B、
B、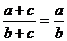
C、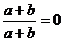 D、
D、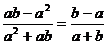
2、纳米是一种长度单位,1纳米 = 10-
A、3.5 ×10-
C、3.5 ×10-
3、下面的表格分别给出了变量x与y之间的对应关系,y与x是反比例函数的是( )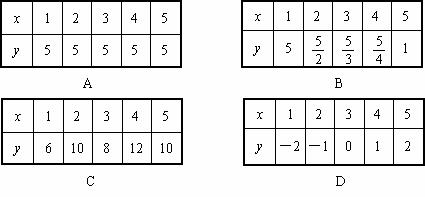
4、要画一个周长是
A、
5、如图,是一次函数y=kx+b与反比例函数y=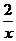 的图像,则关于x的方程kx+b=
的图像,则关于x的方程kx+b=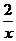 的解为( )
的解为( )
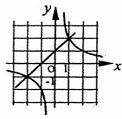
A、xl=1,x2=2 B、xl=―2,x2=―1
C、xl=1,x2=―2 D、xl=2,x2=―1
6、将我省某日11个市、区的最高气温统计如下:
最高气温
市、区个数
1
1
3
1
1
2
1
1
该天这11个市、区最高气温的中位数和众数分别是( )
A、
7、如图,在菱形ABCD中,不一定成立的是( )
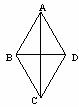
A、四边形ABCD是平行四边形
B、AC⊥BD
C、△ABD是等边三角形
D、∠CAB =∠CAD
8、我国古代数学家赵爽的“勾股圆方图”是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形(如右图所示),如果大正方形的面积是15,小正方形的面积是1,直角三角形的两直角边长分别为a、b,那么(a+b)2的值为( )
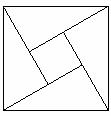
A、16
B、
第 II 卷(非选择题,共96分)
二、填空题:用你敏锐的思维,写出简洁的结果!(本大题共8小题,计24分,只要求填写最后结果,每小题填对得3分)
9、北京2008年第29届奥运会火炬接力活动将历时130天,传递总里程约13.7万千米。传递总里程用科学记数法表示为_____________千米。
10、计算:(―3)―2 = _____________
11、 如图,是甲、乙两地5月下旬平均气温统计图,则甲、乙 两地这10天平均气温的方差大小关系为:s2甲____________s2乙。
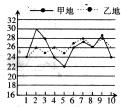
12、老师给出一个函数,甲、乙各指出了这个函数的一个性质:甲:第二、四象限有它的图象;乙:在每个象限内,y随x的增大而增大.
请你写一个满足上述性质的函数表达式______________________
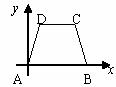
13、如图,在平面直角坐标系中,等腰梯形ABCD的顶点A、B、D的坐标分别是(0,0)、(5,0)、(1,3),则顶点C的坐标是________________________。
14、一组数据35,35,36,36,37,38,38,38,39,40的极差是 ________。
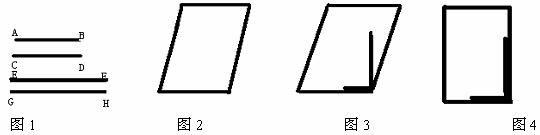
15、工人师傅做铝合金窗框分下面三个步骤进行:
(1)先截出两对符合规格的铝合金窗料,如图1,使AB=CD,EF=GH.
(2)摆成如图2的四边形,则这时窗框的形状是________________形,根据的数学道理是________________________。
(3)将直角尺靠紧窗框的一个角,如图3,调整窗框的边框,当直角尺的两条直角边与窗框无缝隙时,如图4,说明窗框合格,这时窗框是______________,根据的数学道理是___________________。
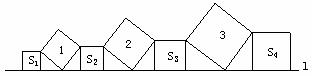
16、在直线 l上依次摆放着七个正方形(如图所示).已知斜放置的三个正方形的面积分别是1、2、3,正放置的四个正方形的面积依次是S1、S2、S3、S4,则S1+S2+S3+S4=_______.
三、解答题:圆满的解答,是你萌动的智慧,相信你一定表现出色!(本大题共8小题,计72分,解答应写出必要的文字说明,证明过程或演算步骤)
17、(本题满分10分)
解分式方程: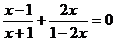
18、(本题满分10分)
请将四个全等直角梯形如图,拼成一个平行四边形,并画出两种不同的拼法示意图(拼出的两个图形只要不全等就认为是不同的拼法)

19、(本题满分10分)
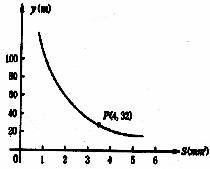
你吃过拉面吗?实际上在做拉面的过程中就渗透着数学知识:一定体积的面团做成拉面,面条的总长度y(m)是面条的粗细(横截面积)S(mm2)的反比例函数,其图象如图所示。
(1)写出y与S的函数关系式。
(2)求当面条粗
20、(本题满分10分)
比邻而居的蜗牛神和蚂蚁王相约,第二天上午8时结伴出发,到相距
21、(本题满分10分)

利用表中提供的数据,解答下列问题:
(1)填写完成下表:
平均成绩
中位数
众数
方差
王军
80
79.5
张成
80
80
(2)请你根据上面的信息,运用所学的统计知识,帮助
22、(本题满分10分)
细心观察左边图,认真分析右边各式,然后解答问题。
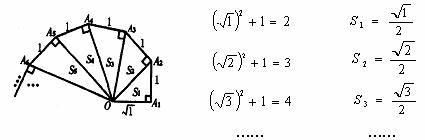
(1)请用含有n(n是正整数)的等式表示上述变化规律。
(2)推算出OA10的长。
(3)求出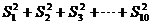 的值。
的值。
23、(本题满分12分)如图所示, 在△ABC中,点O是AC边上的一个动点,过点O作直线MN∥BD,设MN交∠BCA的平分线于点E, 交∠BCA的外角平分线于点F。
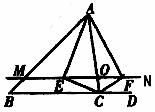
(1)求证:EO = FO。
(2)当点O运动到何处时,四边形AECF是矩形,并加以证明。
(3)满足什么条件时,四边形AECF是正方形,并加以证明。