2007-2008学年度临清市第一学期八年级期末考试
数 学 试 题
一、选择题:下列各题只有一个选项是正确的,请把正确选项的序号涂在答案卡上。每小题4分,共48分。
1.4的平方根是
A.2 B.-
2.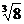 的相反数为
的相反数为
A.2 B.-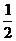 D.
D.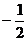
3.下列各式中计算结果等于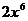 的是
的是
A.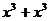 B.
B.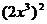 C.
C. D.
D.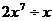
4.在下图右侧的四个三角形中,不能由△ABC经过旋转或平移得到的是

5.如图,该图形围绕自己的旋转中心,按下列角度旋转后,不能与其自身重合的是

A.72° B.108° C.144° D.216°
6.在-3.14,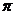 ,
,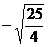 ,
,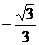 ,
,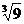 ,
,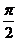 ,
,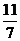 ,-0.1324242424……中,无理数的个数为
,-0.1324242424……中,无理数的个数为
A.2 B.
7.下列计算正确的是
A.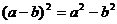 B.
B.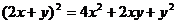
C.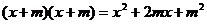 D.
D.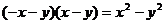
8.有两棵树,一棵高
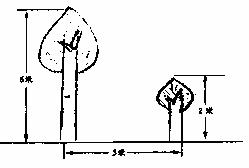
A.5 B.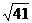 D.不能确定
D.不能确定
9.如图,已知□ABCD中,∠ABC的平分线交AD于点E,且AE=2,DE=1,则□ABCD的周长为
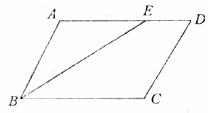
A.8 B.6 C.10 D.不能确定
10.如图,矩形ABCD的周长为20cm,对角线AC、BD相交于点O,OE⊥AC交AD于点E,连接CE,则△CDE的周长为
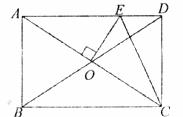
A.5cm B.8cm C.9cm D. 10crn
11.已知□ABCD的两条对角线AC、BD交于点O,且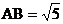 ,AO=2,OB=1,则下列结论不一定成立的是
,AO=2,OB=1,则下列结论不一定成立的是
A.AC⊥BD B.□ABCD的周长为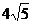
C.□ABCD的面积为8 D.□ABCD为菱形
12.如图,在Rt△ABC中,∠BAC=90°,AB=3,AC=4,将△ABC沿直线BC向右平移2.5个单位得到△DEF,连接AD、AE,则下列结论中不成立的是
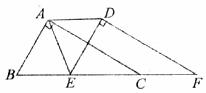
A.AD BE B.∠ABC=∠DEF
BE B.∠ABC=∠DEF
C.ED⊥AC D.△ADE为等边三角形
二、填空题:请将最后结果真接填在答卷上。每小题4分,共20分。
13.如图,数轴上点A和点B之间表示整数的点有 个。
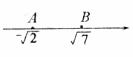
14.多项式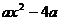 与多项式
与多项式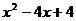 公因式为 。
公因式为 。
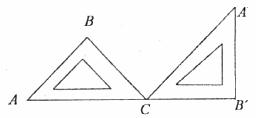
15.如图,一块等腰直角的三角板ABC,在水平桌面上绕点C按顺时针方向旋转到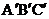 的位置,使A、C、
的位置,使A、C、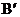 三点共线,那么旋转角度的大小为 。
三点共线,那么旋转角度的大小为 。
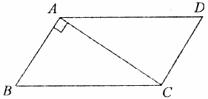
16.如图,□ABCD中,AB=6cm,BC=10cm,且AB⊥AC,则平行线AB、CD间的距离为 ,平行线AD、BC间的距离为 。
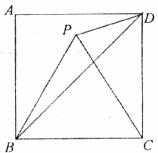
17.如图,四边形ABCD为正方形,△BPC为等边三角形,连接PD、BD,则∠BDP= 。
三、解答题:解答应写出必要的文字说明、证明过程或推演步骤。本题共5个小题,共52分。
18.(本题满分12分)
(1)分解因式:①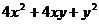 ;②
;②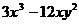
(2)化简求值: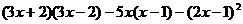 ,其中
,其中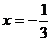 。
。
19.(本题满分8分)
下雨时,常常是先见闪电,后闻雷鸣,这是由于光速比声速快的缘故,已知光在空气中的传播速度约为3×108米/秒,而声音在空气中的传播速度约为3.4×102米/秒。请计算一下,光速是声速的多少倍?(结果保留两个有效数字)
20.(本题满分12分)
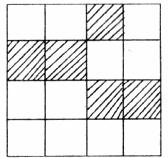
(1)如图,是4×4正方形网格,请在其中选取一个白色的单位正方形并涂黑,使图中黑色部分是一个中心对称图形。
(2)如图,由边长为1的小正方形组成的方格纸中,有两个全等的三角形,即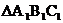 和
和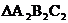 。
。
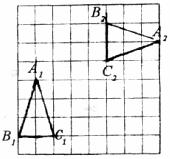
①请你指出在方格纸内如何运用平移、旋转变换,将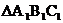 重合到
重合到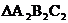 上;
上;
②将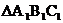 绕点Al逆时针旋转90°,得到
绕点Al逆时针旋转90°,得到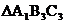 ,请你画出
,请你画出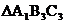 ,并判断
,并判断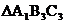 与
与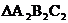 是否成中心对称,若成中心对称,请在图中标出对称中心O。
是否成中心对称,若成中心对称,请在图中标出对称中心O。
21.(本题满分10分)
(1)如图①是一个重要公式的几何解释,请你写出这个公式;
(2)如图②,Rt△ABC≌Rt△CDE,∠B=∠D=90°,并且B、C、D三点共线,试证明∠ACE=90°;
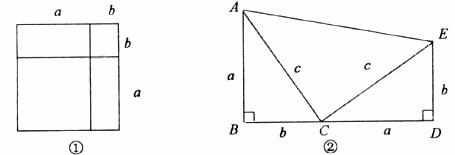
(3)伽菲尔德(Garfield,1881年任美国第20届总统)利用(1)中的公式和图②证明了勾股定理。现请同学们沿着总统的思路,利用图②的面积表示验证勾股定理,请写出验证过程。
22.(本题满分10分)
如图,四边形ABCD是矩形纸片,翻折∠B、∠D使BC、DA恰好落在AC上,设F、H分别是B、D落在AC上的两点,AG、CE为折痕。
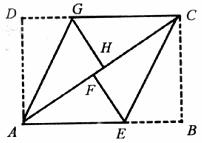
(1)试判断四边形AECG的形状,并说明理由;
(2)若AB=4cm,BC=3cm,求线段EF的长。