2008年北京市丰台区初三年级二模试卷
数学
一、选择题(每小题4分,共32分)
1.下列计算正确的是( )
A.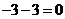 B.
B.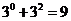 C.
C.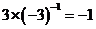 D.
D.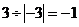
2.北京市申办2008年奥运会,得到了全国人民的热情支持.据统计,某日北京申奥网站的访问人次为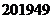 ,用四舍五入法取近似值保留两个有效数字,得( )
,用四舍五入法取近似值保留两个有效数字,得( )
A.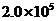 B.
B.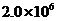 C.
C.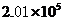 D.
D.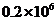
3.某校为了了解240名初三学生的体重情况,从中抽取50名学生进行测量,下列说法正确的是 ( )
A.总体是240 B.样本容量是
4.若分式 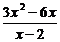 的值为0 ,则
的值为0 ,则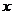 的值为 ( )
的值为 ( )
A.0 B.
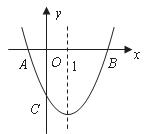
5.已知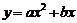 的图象如图所示,则
的图象如图所示,则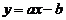 的图象一定过 ( )
的图象一定过 ( )
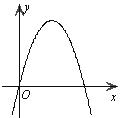
A.第一、二、三象限 B.第一、二、四象限
C.第二、三、四象限 D.第一、三、四象限
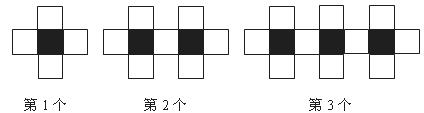
6.用黑白两种颜色的正方形纸片,按黑色纸片数逐渐加1的规律拼成一列图案:请问第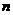 个图案中有白色纸片的张数为(
)
个图案中有白色纸片的张数为(
)
A.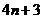 B.
B.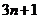 C.
C.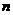 D.
D.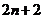
7.如图,将一张等腰直角△ABC纸片沿中位线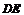 剪开后,可以拼成的四边形是 ( )
剪开后,可以拼成的四边形是 ( )
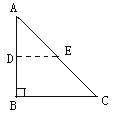
A.矩形或等腰梯形 B.矩形或平行四边形
C.平行四边形或等腰梯形 D.矩形或等腰梯形或平行四边形
8.下列四个展开图中能够构成如图所示模型的是( )
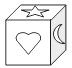
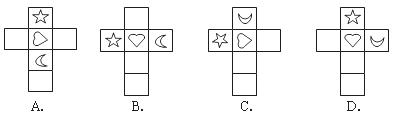
二、填空题(每小题4分,共16分)
9.已知b、m是实数,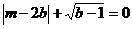 ,则
,则 的值为 .
的值为 .
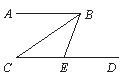
10.如图,已知AB∥CD,∠C=35°,BC平分∠ABE,则∠ABE为 度.
11.假定鸟卵孵化后,雏鸟为雌鸟与为雄鸟的概率相同。如果三枚卵全部成功孵化,则三只雏鸟中恰有两只雄鸟的概率为 .
12.在数学中,为了简便计算记1!=1 ,2!=2×1 ,3!=3×2×1 ,……,
n!= .则
.则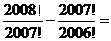 .
.
三、解答题(共5个小题,共24分)
13.(4分)计算: .
.
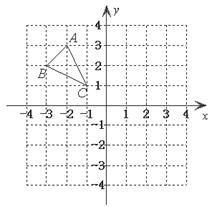
14.(4分)△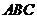 在平面直角坐标系中的位置如图所示,现将△
在平面直角坐标系中的位置如图所示,现将△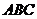 经过两次变换:第一次是作出△
经过两次变换:第一次是作出△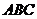 关于
关于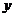 轴对称的△
轴对称的△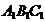 ;再将△
;再将△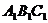 向下平移4个单位长度,得到△
向下平移4个单位长度,得到△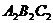 .请你在下面的网格中画出平移后的△
.请你在下面的网格中画出平移后的△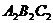 .(不写作法,保留作图痕迹,指明结果)
.(不写作法,保留作图痕迹,指明结果)
15.( 5分)先化简再求值: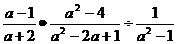 其中
其中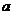 满足
满足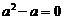 .
.
16.( 5分)为响应承办“绿色奥运”的号召,某班组织部分同学义务植树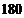 棵,由于同学们的积极参与,实际参加的人数比原计划增加了
棵,由于同学们的积极参与,实际参加的人数比原计划增加了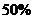 ,结果每人比原计划少栽了
,结果每人比原计划少栽了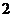 棵,问实际有多少人参加了这次植树活动?
棵,问实际有多少人参加了这次植树活动?
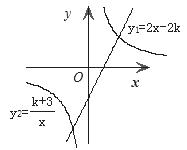
17.( 6分)已知一次函数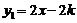 的图象与反比例函数
的图象与反比例函数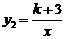 的图象相交,其中一个交点的纵坐标为-4.(1)求两个函数的解析式;(2)结合图象求出当
的图象相交,其中一个交点的纵坐标为-4.(1)求两个函数的解析式;(2)结合图象求出当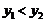 时,
时,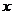 的取值范围.
的取值范围.
18.(本小题满分5分) 已知:关于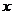 的一元二次方程
的一元二次方程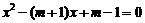 .求证:不论
.求证:不论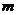 取何值时,方程总有两个不相等的实数根.
取何值时,方程总有两个不相等的实数根.
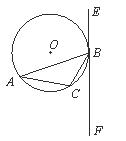
19.(5分)已知:△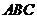 内接于⊙
内接于⊙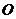 ,过点
,过点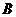 作直线
作直线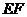 ,
,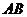 为非直径的弦,且
为非直径的弦,且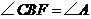 。(1)求证:
。(1)求证: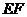 是⊙
是⊙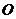 的切线;(2)若
的切线;(2)若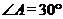 ,
,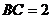 ,联结
,联结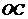 并延长交
并延长交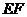 于点
于点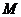 ,求由弧
,求由弧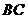 、线段
、线段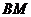 和
和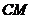 所围成的图形的面积.
所围成的图形的面积.
20.(5分)用两个全等的正方形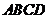 和
和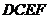 拼成一个矩形
拼成一个矩形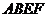 ,把一个足够大的直角三角尺的直角顶点与这个矩形的边
,把一个足够大的直角三角尺的直角顶点与这个矩形的边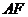 的中点
的中点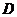 重合,且将直角三角尺绕点
重合,且将直角三角尺绕点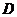 按逆时针方向旋转.
按逆时针方向旋转.
(1)当直角三角尺的两直角边分别与矩形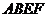 的两边
的两边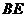 、
、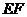 相交于点
相交于点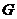 、
、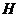 时,(如图甲),通过观察或测量
时,(如图甲),通过观察或测量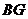 与
与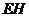 的长度,你能得到什么结论?并证明你的结论.
的长度,你能得到什么结论?并证明你的结论.
(2)当直角三角尺的两直角边分别与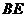 、
、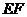 的延长线相交于点
的延长线相交于点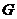 、
、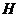 时(如图乙),你在图甲中得到的结论还成立吗?简要说明理由.
时(如图乙),你在图甲中得到的结论还成立吗?简要说明理由.
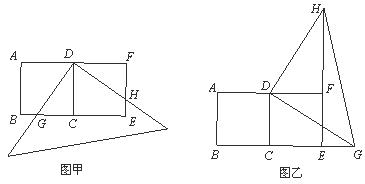
解:(1)得到的结论是 .
(2)得到的结论 .(填写“成立”、“不成立”)
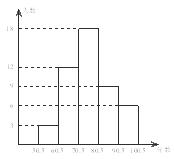
21.(6分)某校九年级一班数学调研考试成绩绘制成频数分布直方图,如图(得分取整数).请根据所给信息解答下列问题:(1)这个班有多少人参加了本次数学调研考试?(2)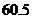 ~
~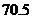 分数段的频数和频率各是多少?(3)请你根据统计图,提出一个与(1),(2)不同的问题,并给出解答.
分数段的频数和频率各是多少?(3)请你根据统计图,提出一个与(1),(2)不同的问题,并给出解答.
22.(5分)如图,梯形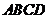 中,
中,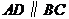 ,
,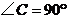 ,且
,且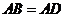 .联结
.联结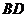 ,过点
,过点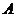 作
作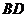 的垂线,交
的垂线,交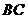 于点
于点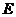 ,垂足为
,垂足为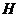 .如果
.如果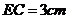 ,
,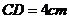 ,求梯形
,求梯形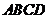 的面积.
的面积.

23.(6分)为保证交通安全,汽车驾驶员必须知道汽车刹车后的停止距离(开始刹车到车辆停止车辆行驶的距离)与汽车行驶速度(开始刹车时的速度)的关系,以便及时刹车.下表是某款车在平坦道路上, 路况良好时刹车后的停止距离与汽车行驶速度的对应值表:
行驶速度(千米/时)
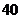
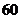
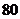

停止距离(米)
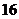
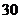
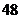

(1)设汽车刹车后的停止距离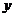 (米)是关于汽车行驶速度
(米)是关于汽车行驶速度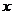 (千米/时)的函数,给出以下三个函数:①
(千米/时)的函数,给出以下三个函数:①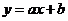 ;②
;②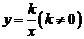 ;③
;③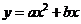 ,请选择恰当的函数来描述停止距离
,请选择恰当的函数来描述停止距离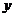 (米)与汽车行驶速度
(米)与汽车行驶速度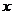 (千米/时)的关系,说明选择理由,并求出符合要求的函数的解析式;(2)如果汽车刹车后的停止距离为
(千米/时)的关系,说明选择理由,并求出符合要求的函数的解析式;(2)如果汽车刹车后的停止距离为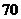 米,那么根据你所选择的函数解析式,求汽车的行驶速度.
米,那么根据你所选择的函数解析式,求汽车的行驶速度.
24.( 8分)抛物线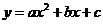 交
交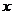 轴于
轴于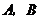 两点,交
两点,交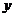 轴于点
轴于点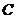 ,对称轴为直线
,对称轴为直线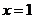 。且A、C两点的坐标分别为
。且A、C两点的坐标分别为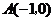 ,
, .(1)求抛物线
.(1)求抛物线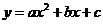 的解析式;(2)求
的解析式;(2)求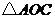 和
和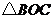 的面积的比;(3)在对称轴上是否存在一个点
的面积的比;(3)在对称轴上是否存在一个点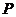 ,使
,使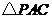 的周长最小.若存在,请求出点
的周长最小.若存在,请求出点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
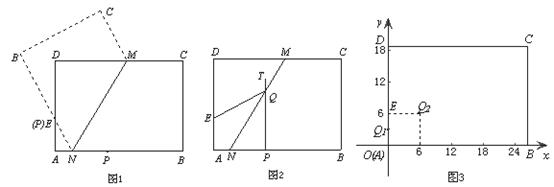
25.(8分)已知:矩形纸片 中,
中,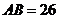 厘米,
厘米,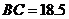 厘米,点
厘米,点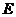 在
在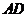 上,且
上,且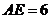 厘米,点
厘米,点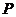 是
是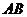 边上一动点.按如下操作:步骤一,折叠纸片,使点
边上一动点.按如下操作:步骤一,折叠纸片,使点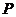 与点
与点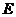 重合,展开纸片得折痕
重合,展开纸片得折痕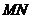 (如图1所示);步骤二,过点
(如图1所示);步骤二,过点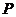 作
作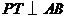 ,交
,交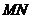 所在的直线于点
所在的直线于点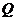 ,联结
,联结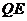 (如图2所示)(1)无论点
(如图2所示)(1)无论点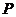 在
在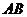 边上任何位置,都有
边上任何位置,都有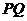
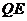 (填“
(填“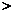 ”、“
”、“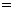 ”、“
”、“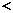 ”号);
”号);
(2)如图3所示,将纸片 放在直角坐标系中,按上述步骤一、二进行操作:①当点
放在直角坐标系中,按上述步骤一、二进行操作:①当点 在
在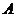 点时,
点时,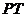 与
与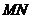 交于点
交于点 ,
, 点的坐标是( , );
点的坐标是( , );
②当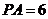 厘米时,
厘米时,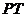 与
与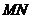 交于点
交于点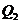 ,
,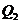 点的坐标是( , );
点的坐标是( , );
③当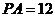 厘米时,在图3中画出
厘米时,在图3中画出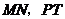 (不写画法),并求出
(不写画法),并求出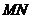 与
与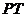 的交点
的交点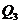 的坐标;
的坐标;
(3)点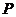 在运动过程,
在运动过程,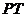 与
与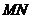 形成一系列的交点
形成一系列的交点 观察、猜想:众多的交点形成的图象是什么?并直接写出该图象的函数表达式,及自变量的取值范围.
观察、猜想:众多的交点形成的图象是什么?并直接写出该图象的函数表达式,及自变量的取值范围.