2008年湖北省襄樊市初中毕业、升学统一考试
数学试卷
一、选择题:本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的,请将其序号在答题卡上涂黑作答.
1.2的相反数是( )
A.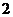 B.
B.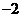 C.
C.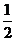 D.
D.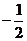
2.下列运算正确的是( )
A.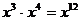 B.
B.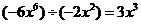
C.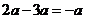 D.
D.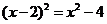
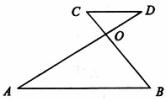
3.如图,已知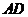 与
与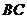 相交于点
相交于点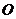 ,
,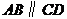 ,如果
,如果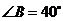 ,
,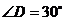 ,则
,则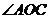 的大小为( )
的大小为( )
A.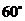 B.
B.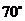 C.
C.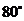 D.
D.
4.下列说法正确的是( )
A.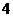 的平方根是
的平方根是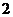 B.将点
B.将点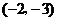 向右平移5个单位长度到点
向右平移5个单位长度到点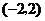
C. 是无理数 D.点
是无理数 D.点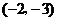 关于
关于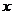 轴的对称点是
轴的对称点是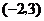
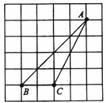
5.在正方形网格中,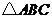 的位置如图所示,则
的位置如图所示,则 的值为( )
的值为( )
A.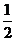 B.
B.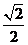 C.
C.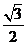 D.
D.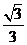
6.某种商品零售价经过两次降价后的价格为降价前的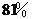 ,则平均每次降价(
)
,则平均每次降价(
)
A.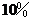 B.
B.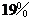 C.
C.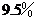 D.
D.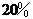
7.顺次连接等腰梯形四边中点所得四边形是( )
A.菱形 B.正方形 C.矩形 D.等腰梯形
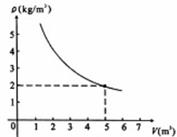
8.在一个可以改变体积的密闭容器内装有一定质量的二氧化碳,当改变容器的体积时,气体的密度也会随之改变,密度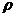 (单位:kg/m3)是体积
(单位:kg/m3)是体积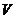 (单位:m3)的反比例函数,它的图象如图所示,当
(单位:m3)的反比例函数,它的图象如图所示,当 时,气体的密度是(
)
时,气体的密度是(
)
A.
9.如图,是一个由若干个相同的小正方体组成的几何体的三视图,则组成这个几何体的小正方体的个数是( )
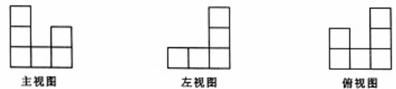
A.7个 B.8个 C.9个 D.10个
10.如图,扇形纸扇完全打开后,外侧两竹条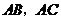 夹角为
夹角为 ,
,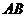 的长为
的长为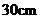 ,贴纸部分
,贴纸部分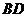 的长为
的长为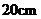 ,则贴纸部分的面积为(
)
,则贴纸部分的面积为(
)

A.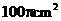 B.
B.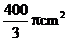
C. D.
D.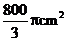
二、填空题:本大题共6小题,每小题3分,共18分.把答案填在答题卡的相应位置上.
11.一方有难,八方支援.截至6月3日12时,中国因汶川大地震共接受国内外捐赠款物423.64亿元,用科学记数法表示为 元.
12.如图,⊙O中 ,
, ,则
,则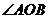 的度数为
.
的度数为
.

13.当 时,关于
时,关于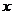 的分式方程
的分式方程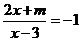 无解.
无解.
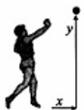
14.如图,一名男生推铅球,铅球行进高度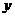 (单位:m)与水平距离
(单位:m)与水平距离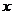 (单位:m)之间的关系是
(单位:m)之间的关系是 .则他将铅球推出的距离是
m.
.则他将铅球推出的距离是
m.
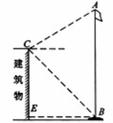
15.如图,张华同学在学校某建筑物的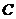 点处测得旗杆顶部
点处测得旗杆顶部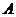 点的仰角为
点的仰角为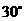 ,旗杆底部
,旗杆底部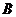 点的俯角为
点的俯角为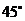 .若旗杆底部
.若旗杆底部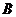 点到建筑物的水平距离
点到建筑物的水平距离 米,旗杆台阶高1米,则旗杆顶点
米,旗杆台阶高1米,则旗杆顶点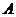 离地面的高度为
米(结果保留根号).
离地面的高度为
米(结果保留根号).
16.如图,在锐角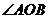 内部,画1条射线,可得3个锐角;画2条不同射线,可得6个锐角;画3条不同射线,可得10个锐角;……照此规律,画10条不同射线,可得锐角
内部,画1条射线,可得3个锐角;画2条不同射线,可得6个锐角;画3条不同射线,可得10个锐角;……照此规律,画10条不同射线,可得锐角
个.

三、解答题:本大题共9小题,共72分.解答应写出文字说明,证明过程或演算步骤,并且写在答题卡上每题对应的答题区域内.
17.(本小题满分7分)
化简求值: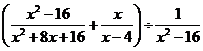 ,其中
,其中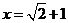 .
.
18.(本小题满分6分)
为了了解学生课业负担情况,某初中在本校随机抽取50名学生进行问卷调查,发现被抽查的学生中,每天完成课外作业时间,最长不足120分钟,没有低于40分钟的.并将抽查结果绘制成了一个不完整的频数分布直方图,如图所示.
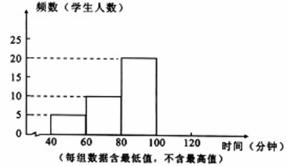
(1)请补全频数分布直方图;
(2)被调查50名学生每天完成课外作业时间的中位数在 组(填时间范围);
(3)若该校共有1200名学生,请估计该校大约有 名学生每天完成课外作业时间在80分钟以上(包括80分钟).
19.(本小题满分6分)
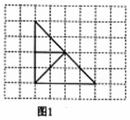
如图1,方格纸中有一透明等腰三角形纸片,按图中裁剪线将这个纸片裁剪成三部分.请你将这三部分小纸片重新分别拼接成;(1)一个非矩形的平行四边形;(2)一个等腰梯形;(3)一个正方形.请在图11-2中画出拼接后的三个图形,要求每张三角形纸片的顶点与小方格顶点重合.

20.(本小题满分7分)
如图,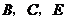 是同一直线上的三个点,四边形
是同一直线上的三个点,四边形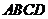 与四边形
与四边形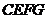 都是正方形.连接
都是正方形.连接 .
.
(1)观察猜想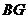 与
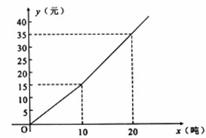
与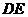 之间的大小关系,并证明你的结论;
之间的大小关系,并证明你的结论;
(2)图中是否存在通过旋转能够互相重合的两个三角形?若存在,请指出,并说出旋转过程;若不存在,请说明理由.
21.(本小题满分7分)
在一个不透明的布袋中有4个完全相同的乒乓球,把它们分别标号为1,2,3,4,随机地摸出一个乒乓球然后放回,再随机地摸出一个乒乓球.求下列事件的概率:
(1)两次摸出的乒乓球的标号相同;
(2)两次摸出的乒乓球的标号的和等于5.
22.(本小题满分7分)
“六一”儿童节前夕,某消防队官兵了解到汶川地震灾区一帐篷小学的小朋友喜欢奥运福娃,就特意购买了一些送给这个小学的小朋友作为节日礼物.如果每班分10套,那么余5套;如果前面的班级每个班分13套,那么最后一个班级虽然分有福娃,但不足4套.问:该小学有多少个班级?奥运福娃共有多少套?
23.(本小题满分10分)
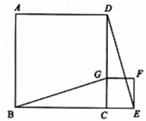
我国是世界上严重缺水的国家之一.为了增强居民节水意识,某市自来水公司对居民用水采用以户为单位分段计费办法收费.即一月用水10吨以内(包括10吨)的用户,每吨收水费 元;一月用水超过10吨的用户,10吨水仍按每吨
元;一月用水超过10吨的用户,10吨水仍按每吨 元收费,超过10吨的部分,按每吨
元收费,超过10吨的部分,按每吨 元(
元( )收费.设一户居民月用水
)收费.设一户居民月用水 吨,应收水费
吨,应收水费 元,
元, 与
与 之间的函数关系如图所示.
之间的函数关系如图所示.
(1)求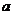 的值;某户居民上月用水8吨,应收水费多少元?
的值;某户居民上月用水8吨,应收水费多少元?
(2)求 的值,并写出当
的值,并写出当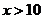 时,
时,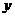 与
与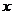 之间的函数关系式;
之间的函数关系式;
(3)已知居民甲上月比居民乙多用水4吨,两家共收水费46元,求他们上月分别用水多少吨?
24.(本小题满分10分)
如图,直线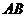 经过⊙O上的点
经过⊙O上的点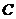 ,并且
,并且 ,
,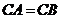 ,
,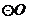 交直线
交直线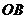 于
于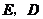 ,连接
,连接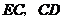 .
.
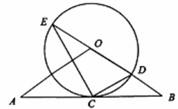
(1)求证:直线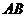 是⊙O的切线;
是⊙O的切线;
(2)试猜想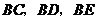 三者之间的等量关系,并加以证明;
三者之间的等量关系,并加以证明;
(3)若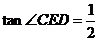 ,⊙O的半径为3,求
,⊙O的半径为3,求 的长.
的长.
25.(本小题满分12分)
如图,四边形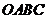 是矩形,
是矩形, ,
,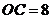 ,将矩形
,将矩形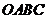 沿直线
沿直线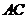 折叠,使点
折叠,使点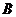 落在
落在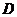 处,
处,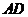 交
交 于
于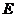 .
.

(1)求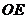 的长;
的长;
(2)求过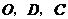 三点抛物线的解析式;
三点抛物线的解析式;
(3)若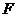 为过
为过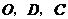 三点抛物线的顶点,一动点
三点抛物线的顶点,一动点 从点
从点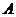 出发,沿射线
出发,沿射线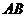 以每秒1个单位长度的速度匀速运动,当运动时间
以每秒1个单位长度的速度匀速运动,当运动时间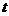 (秒)为何值时,直线
(秒)为何值时,直线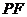 把
把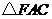 分成面积之比为
分成面积之比为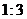 的两部分?
的两部分?