1．下列各式中，与是同类根式的是

A．                         B．24                       C．                         D．

2．图1a所示几何体的左视图是图1b中的

3．下列成语所描述的事件是必然事件的是

A．水中捞月                                               B．拔苗助长

C．守株待兔                                               D．瓮中捉鳖

4．如图2所不，把直线向上平移2个单位得到直线，则的表达式为

A．                                             B．

C．                                            D．

5．图3是5个城市的国际标准时间（单位：时），那么北京时间2007年6月17 日上午9时应是

A．伦敦时间2007年6月17日凌晨1时

B．纽约时间2007年6月17日晚上22时

C．多伦多时间2007年6月16日晚上20时

D．汉城时间2007年6月17日上午8时

  6．某公园计划砌一个形状如图4a所示的喷水池，后来有人建议改为图4b的形状，且外圆的直径不变，喷水池边沿的宽度、高度不变，你认为砌喷水池的边沿

A．图5a需要的材料多                                B．图5b需要的材料多

C．图5a、图5b需要的材料一样多              D．无法确定

7．用直尺和圆规作一个角等于已知角的示意图如图5所示，则说明的依据是

A．（SSS）               B．（SAS）               C．（ASA）                 D．（AAS）

8．图6是一台54英寸的大背投彩电放置在墙角的俯视图。设∠DAO=α，彩电后背AD平行于前沿BC，且与BC的距离为60cm，若AO=100cm，则墙角O到前沿BC的距离OE是

A．（60+100sinα）cm                                   B．（60+100cosα）cm

C．（60+100tanα）cm                                     D．以上答案都不对

9．如图7a所示，在物理实验课上，小明用弹簧秤将铁块A悬于盛有水的水槽中，然后匀速向上提起，直至铁块完全露出水面一定高度，则弹簧秤的读数（单位：N）与铁块被提起的高度（单位：cm）之间的函数关系的大致图像是图7b中的

10．探索规律：根据图8a中箭头指向的规律，从2005到2006再到2007，箭头的方向是图8b中的

11．某中学为了解学生上学方式，现随机抽取部分学生进行调查，将结果绘成条形统计图如图9所示，由此可估计该校2400名学生中有         名学生是乘车上学的。

12．如图10，一束光线照在坡度为1∶的斜坡上，被斜坡上的平面镜反射成与地面平行的光线。则这束与坡面的夹角α是          度。

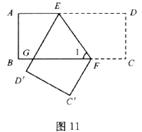
13．如图11，把一张长方形纸条ABCD沿EF折叠，若∠1=58°，则∠AEG=         。

第Ⅱ卷（共118分）

14．在位于O处某海防哨所的北偏东60°相距6海里的A处，有一艘快艇正向正南方向航行，经过一段时间快艇到达哨所东偏南45°的B处，则A、B间的距离是       海里。（精确到0.1海里，≈1.414，≈1.732）

15．如图12所示，一次函数与反比例函数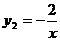的图像交于点A（－2，1），B（1，－2），则使的上的取值范围是           。

16．如图13所示，矩形内两相邻正方形的面积分别是2和6，那么矩形内阴影部分的面积是          （结果可用根号表示）。

17．如图14，在平台上用直径100m的两根圆钢棒嵌在大型工件的两侧，测量大的圆形工件的直径D，测得两根圆钢棒外侧距离为400mm，则工件的直径D（mm）用科学记数法可写为            （图中显示为两根圆钢棒的圆心距为4000mm）。

18．观察表1，寻找规律，表2是从表1中截取的一部分，其中a，b，c的值分别为

19．（本题满分6分）如图15所示，数轴上点A表示，点A关于原点的对称点为B，设点B所表示的数为，求的值。

20．（本题满分7分）

解方程组：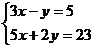

21．（本题满分7分）

化简并求值：，其中，。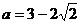

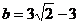22．（本题10分）

某学校举行演讲比赛，选出了10名同学担任评委，并事先拟定从如下4个方案中选择合理的方案来确定每个演讲者的最后得分（满分为10分）：

方案1：所有评委所给分的平均数。

方案2：在所有评委所给分中，去掉一个最高分和一个最低分，然后再计算其余给分的平均数。

方案3：所有评委所给分的中位数。

方案4：所有评委所给分的众数。

为了探究上述方案的合理性，先对某个同学的演讲成绩进行了统计实验。下面是这个同学的得分统计图：

（1）分别按上述4个方案计算这个同学演讲的最后得分。

（2）根据（1）中的结果，请用统计的知识说明哪些方案不适合作为这个同学演讲的最后得分。

23．（本题满分10分）

扬子江药业集团生产的某种药品包装盒的侧面展开图如图17所示。如果长方体盒子的长比宽多4cm，求这种药品包装盒的体积。

24．（本题满分10分）

三人相互传球，由甲开始发球，并作为第一次传球。

（1）用列表或画树状图的方法求经过3次传球后，球仍回到甲手中的概率是多少?

（2）由（1）进一步探索：经过4次传球后，球仍回到甲手中的不同传球的方法共有多少种?

（3）就传球次数n与球分别回到甲、乙、丙手中的可能性大小，提出你的猜想（写出结论即可）。

25．（本题满分10分）

一商场计划到计算器生产厂家购进一批A、B两种型号的计算器。经过商谈，A型计算器单价为50元，100只起售，超过100只的部分，每只优惠20%；B型计算器单价为22元，150只起售，超过150只的超过部分，每只优惠2元。如果商家计划购进计算器的总量既不少于700只，又不多于800只，且分别用于购买A、B这两种型号的计算器的金额相等，那么该商场至少需要准备多少资金?

26．（本题满分8分）

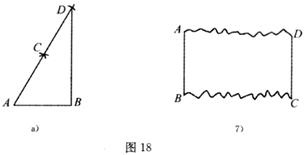
某中学师生在劳动基地活动时，看到木工师傅在材料边角处画直角时，用了一种“三弧法”，如图18a所示．方法是：

①画线段AB，分别以A，B为圆心，AB长为半径画弧相交于C；

②以C为圆心，仍以AB长为半径画弧交AC的延长线于D；

③连接DB。

则∠ABD就是直角。

（1）请你就∠ABD是直角作出合理解释。

（2）现有一长方形木块的残留部分如图18b，其中AB，CD整齐且平行，BC，AD是参差不齐的毛边。请你在毛边附近用尺规画一条与AB，CD都垂直的边（不写作法，保留作图痕迹）。

27．（本题满分13分）

如图19所示，足球场上守门员在O处开出一高球，球从离地面1m的A处飞出（A在轴上），运动员乙在距O点6m的B处发现球在自己头的正上方达到最高点M，距地面约4m高，球落地后又一次弹起。据实验，足球在草坪上弹起后的抛物线与原来的抛物线形状相同，最大高度减少到原来最大高度的一半。

（1）求足球开始飞出到第一次落地时，该抛物线的表达式。

（2）足球第一次落地点C距守门员多少米?（取）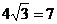

（3）运动员乙要抢到第二个落点D，他应再向前跑多少米?（取）

28．（本题13分）

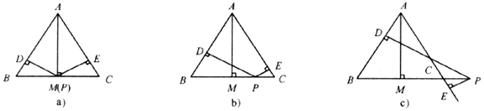
如图20，已知等边△ABC和点P，设点P到∠ABC三边AB、AC、BC（或其延长线）的距离分别为h₁、h₂、h₃，△ABC的高为h。

在图a中，点P是边BC的中点，此时h₃=0，可得结论：h₁+h₂+h₃=h。在图b～e中，点P分别在线段MC上、MC延长线上、△ABC内、△ABC外。

（1）请探究：图b～e中，h₁、h₂、h₃、h之间的关系。（直接写出结论）

（2）证明图b所得结论。

（3）证明图d所得结论。

（4）在图f中，若四边形RBCS是等腰梯形，∠B=∠C=60°，RS=n，BC=m，点P在梯形内，且点P到四边BR、RS、SC、CB的距离分别是h₁、h₂、h₃、h₄，梯形的高为h，则h₁、h₂、h₃、h₄、h之间的关系为：         ；图d与图f中的等式有何关系?