2008年江苏省启东中学中考模拟考试(九)
数学试卷
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷两部分
第Ⅰ卷(选择题,共32分)
一、选择题(本题共10小题;第1~8题每小题3分,第9~10题每小题4分,共32分)下列各题都有代号为A、B、C、D的四个结论供选择,其中只有一个结论是正确的.
1.已知某种型号的纸100张厚度约为
A.1.3×
C.1.3×
2.方程 的正根为 ( )
的正根为 ( )
A. B.
B. C.
C. D.
D.
3.在图所示的四个图案中,既是轴对称图形,又是中心对称图形的是 ( )

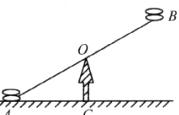
4.如图所示,是跷跷板示意图,横板AB绕中点O上下转动,立柱OC与地面垂直,当横板AB的A端着地时,测得∠OAC=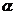 ,则在玩跷跷板时,上下最大可以转动的角度为 ( )
,则在玩跷跷板时,上下最大可以转动的角度为 ( )
A.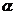 B.
B.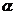 C.90°-
C.90°-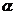 D.90°+
D.90°+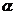
5.某快餐店用米饭加不同炒菜配制了一批盒饭,配土豆丝炒肉的有25盒,配芹菜炒肉丝的有30盒,配辣椒炒鸡蛋的有10盒,配芸豆炒肉片的有15盒.每盒盒饭的大小、外形都相同,从中任选一盒,不含辣椒的概率是 ( )
A.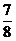 B.
B.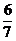 C.
C.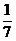 D.
D.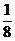
6.若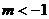 ,则下列函数①
,则下列函数①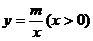 ,②
,②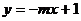 ,③
,③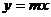 ,④
,④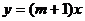 中,y的值随
中,y的值随 的值增大而增大的函数共有 ( )
的值增大而增大的函数共有 ( )
A.1个 B.2个 C.3个 D.4个
7.图a是某一立方体的侧面展开图,则该立方体是图b中 ( )

8.如图的图形:

其中,阴影部分的面积相等的是 ( )
A.①② B.②③ C.③④ D.④①
9.用甲、乙两种原料配制成某种饮料,已知这两种原料的维生素C含量及购买这两种原料的价格如下表:
甲种原料
乙种原料
维生素C含量/(单位/kg)
600
100
原料价格/(元/kg)
8
4
现配制这种饮料10kg,要求至少含有4200单位的维生素C,若所需甲种原料的质量为 kg,则
kg,则 应满足的不等式为 ( )
应满足的不等式为 ( )
A.600 +100(10-
+100(10- )≥4200 B.8
)≥4200 B.8 +4(100-
+4(100- )≤4200
)≤4200
C.600 +100(10-
+100(10- )≤4200 D.8
)≤4200 D.8 +4(100-
+4(100- )≥4200
)≥4200
10.如图,正方形ABCD的边长为2,点E在AB边上.四边形EFGB也为正方形,设△AFC的面积为S,则 ( )

A.S=2 B.S=2.4 C.S=4 D.S与BE长度有关
第Ⅱ卷(共118分)
二、填空题(本大题共6小题,每小题3分,共18分,把答案填写在题中的横线上.)
11.计算: .
.
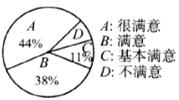
12.某商场为了解本商场服务质量,随机调查了来本商场的200名顾客,调查的结果如图所示,根据图中给出的信息,这200名顾客中对该商场的服务质量表示不满意的有 名.
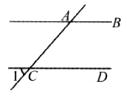
13.如图,已知AB//CD,若∠1=50°,则∠BAC= .
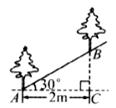
14.如图所示,沿倾斜角为30°的山坡植树,要求相邻两棵树的水平距离AC为2m,那么相邻两棵树的斜坡距离AB约为 m.(精确到0.1m,可能用到的数据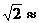 1.41,
1.41,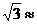 1.73).
1.73).
15.两圆有多种位置关系,图中不存在的位置关系是 .
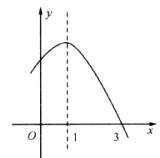
16.已知二次函数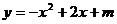 的部分图像如图所示,则关于
的部分图像如图所示,则关于 的一元二次方程
的一元二次方程
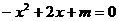 的解为
.
的解为
.
17.将矩形纸片ABCD如图所示那样折叠,便顶点B与顶点D重合,折痕为EF,若AB=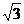 ,AD=3,则△DFF的周长为
.
,AD=3,则△DFF的周长为
.
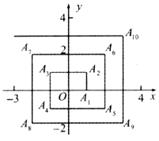
18.如图所示,已知A1(1,0)、A2(1,1)、A3(-1,1)、A4(-1,-l)、A5(2,-1)、…则点A2007的坐标为 .
三、解答题(本大题共10小题,满分84分.解答应写出必要的文字说明、证明过程或推演步骤)
19.(本小题满分6分)解分式方程: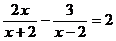
20.(本小题满分6分)解不等式组: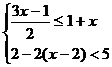 ①②
①②
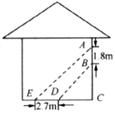
21.如图,阳光通过窗口照射到室内(太阳光线是平行光线),在地面上留下2.7m宽的亮区(如图所示),已知亮区到窗口下墙脚的距离EC=8.7m,窗口高AB=1.8m,求窗口底边离地面的高BC.
22.(本题10分)甲、乙两支篮球队在集训期内进行了五场比赛,将比赛成绩进行统计后, 绘制成如图1、图2的统计图.
(1)在图2中画出折线表示乙队在集训期内这五场比赛成绩的变化情况;
(2)已知甲队五场比赛成绩的平均分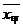 =90分,清你计算乙队五场比赛成绩的平均分
=90分,清你计算乙队五场比赛成绩的平均分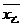 .
.
(3)就这五场比赛,分别计算两队成绩的极差.
(4)如果从甲、乙两队中选派一支球队参加篮球锦标赛,根据上述统计情况,试从平均分、折线的走势、获胜场数和极差四个方面分别进行简要分析,你认为选派哪支球队参赛更能取得好成绩?
23.(本小题满分8分)已知:如图所示,以△ABC的边AB为直径的⊙O交边AB于点D,且过点D的切线DE平分边BC.
(1)BC与⊙O是否相切?请说明理由.
(2)当△ABC满足什么条件时,以点O,B,E,D为顶点的四边形是平行四边形?并说明理由.

24.(本小题满分10分)东方专卖店专销某种品牌的计算器,进价12元/只,售价20元/ 只.为了促销,专卖店决定凡是买10只以上的,就按 (购买量-10)的方式来降低单只的售价(例如,某人买20只计算器,于是每只降价0.10×(20-10)=1元,就可以按19元/只的价格购买),但是最低价为16元/只.
(购买量-10)的方式来降低单只的售价(例如,某人买20只计算器,于是每只降价0.10×(20-10)=1元,就可以按19元/只的价格购买),但是最低价为16元/只.
(1)求顾客一次至少买多少只,才能以最低价购买?
(2)写出当一次购买 只时(
只时( >10),利润y(元)与购买量
>10),利润y(元)与购买量 (只)之间的函数关系式.
(只)之间的函数关系式.
(3)有一天,一位顾客买了46只,另一位顾客买了50只,专卖店发现卖了50只反而比卖46只赚得钱少,为了使每次卖得多赚钱也多,在其他促销条件不变的情况下,最低价16元/只至少要提高到多少?为什么?
25.(本题12分)(1)在图16,17,18中,给出平行四边形ABCD的顶点A,B,D的坐标(如图所示),写出图16,17,18中的顶点C的坐标,它们分别是(5,2), ,

(2)在图19中,给出平行四边形ABCD的顶点A,B,D的坐标(如图所示),求出顶点C的坐标(C点坐标用含a,b,c,d,e,f的代数式表示);

归纳与发现.
(3)通过对图16,17,18,19的观察和顶点C的坐标的探究,你会发现:无论平行四边形ABCD处于直角坐标系中哪个位置,当其顶点坐标为A( ),B(
),B( ),C(
),C( ),D(
),D( )(如图19)时,则四个顶点的横坐标
)(如图19)时,则四个顶点的横坐标 之间的等量关系为 ;纵坐标
之间的等量关系为 ;纵坐标 之间的等量关系为 (不必证明).
之间的等量关系为 (不必证明).
运用与推广
(4)在同一直角坐标系中有抛物线 和三个点G(
和三个点G( ),S(
),S( ),H(
),H( )(其中
)(其中 ).问当c为何值时,该抛物线上存在点P,使得以G,S,H,P为顶点的四边形是平行四边形?并求出所有符合条件的P点坐标.
).问当c为何值时,该抛物线上存在点P,使得以G,S,H,P为顶点的四边形是平行四边形?并求出所有符合条件的P点坐标.
26.(本小题满分11分)如图所示,已知直角坐标系中一条圆弧经过正方形网格的格点A、B、C
(1)用直尺画出该圆弧所在圆的圆心M的位置.
(2)若A点的坐标为(0,4),D点的坐标为(7,0),试验证点D是否在经过点A、B、C的抛 物线上.
(3)在(2)的条件下,求证直线CD是⊙M的切线。
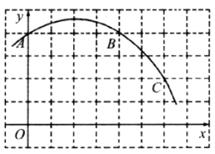
27.(本小题满分11分)
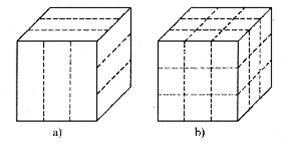
有一块表面是咖啡色,内部是白色,形状是正方体的烤面包,小明用刀在它的上表面、 前表面和右侧表面沿虚线各切两刀,如图a所示,将它切成若干块小正方体形面包,如图b所示.
(1)小明从若干块小面包中任取一块,求该块面包有且只有两个面是咖啡色的概率.
(2)小明和弟弟边吃边玩,游戏规则是:从中任取一块小面包,若它有奇数个面为咖啡色时,小明赢;否则弟弟赢.你认为这样的游戏规则公平吗?为什么?如果不公平,请你修改游戏规则,使之公平.
28.(本小题满分12分)
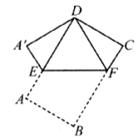
如图所示,四边形OABC是一张放在平面直角坐标系中的正方形纸片.点O与坐标原点重合,点A在 轴上,点C在y轴上,OC=4,点E为BC的中点,点N的坐标为(3,0),过点N且平行于y轴的直线MN与EB交于点M.现将纸片折叠,使顶点C落在MN上,并与MN上的点G重合,折痕为EF,点F为折痕与y轴的交点。
轴上,点C在y轴上,OC=4,点E为BC的中点,点N的坐标为(3,0),过点N且平行于y轴的直线MN与EB交于点M.现将纸片折叠,使顶点C落在MN上,并与MN上的点G重合,折痕为EF,点F为折痕与y轴的交点。
(1)求点G的坐标.
(2)求折痕EF所在直线的解析式.
(3)设点P为直线EF上的点,是否存在这样的点P,使得以P,F,G为顶点的三角形为等腰三角形,若存在,请直接写出点P的坐标;若不存在,请说明理由.