2008年江苏省启东中学中考模拟考试(八)
数学试卷
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷两部分
第Ⅰ卷(选择题,共32分)
一、选择题(本题共10小题;第1~8题每小题3分,第9~10题每小题4分,共32分)下列各题都有代号为A、B、C、D的四个结论供选择,其中只有一个结论是正确的.
1.下列计算正确的是 ( )
A. B.
B. C.
C. D.
D.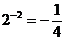
2.把多项式 分解因式的结果是 ( )
分解因式的结果是 ( )
A.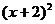 B.
B. C.
C. D.
D.
3.观察统计图,下列结论正确的是 ( )
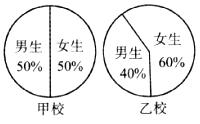
A.甲校女生比乙校女生少 B.乙校男生比甲校男生少
C.乙校女生比甲校男生多 D.甲、乙两校女生人数无法比较
4.函数 与
与 在同一坐标系中图像可能是图中的 ( )
在同一坐标系中图像可能是图中的 ( )

5.某城市计划经过两年的时间,将城市绿地面积从今年的144万m2提高到225万m2,则每年平均增长 ( )
A.15% B.20% C.25% D.30%
6.图a是由几个小立方块搭成的几何体的俯视图,小正方形中的数字表示在该位置的小立方块的个数,那么这个几何体的主视图是图b中的 ( )

7.小明和小亮口袋里都放有五张不同的2008北京奥运会福娃纪念卡,小明从口袋里摸出一张福娃贝贝,小亮从口袋里摸出一张福娃也是贝贝的概率是 ( )

A. B.
B. C.
C. D.
D.
8.
A.自行车 B.汽车 C.磁悬浮列车 D.飞机
9.每位同学都能感受到日出时美丽的景色,如图是一位同学从照片上剪切下来的画面, “图上”太阳与海平线交于A、B两点,他测得“图上”圆的半径为

A.0.
10.如图所示,有六个等圆按甲、乙、丙三种形式摆放,使相邻两圆互相外切,圆心连线分别构成正六边形、平行四边形、正三角形.圆心连线外侧的六个扇形(阴影部分)的面积之和依次记为S,P,Q,则 ( )

A.S>P>Q B.S>Q>P C.S>P=Q D.S=P=Q
第Ⅱ卷(共118分)
二、填空题(本大题共6小题,每小题3分,共18分,把答案填写在题中的横线上.)
11.北京与纽约的时差为-13(负号表示同一时刻纽约时间比北京时间晚).如果现在是北京时间15:00,那么纽约时间是 .
12.某公司销售人员的个人月收入与其每月的销售量成一次函数关系,图像如图所示, 则此销售人员的销售量为3千件时的月收入是 元.

13.如图所示,在世界杯足球比赛中,甲带球向对方球门PQ进攻.当他带球冲到A点时,同伴乙已经助攻冲到B点,有两种射门方式:第一种是甲直接射门;第二种是甲将球传给乙,由乙射门.仅从射门角度考虑,应选择 种射门方式.

14.如图所示,A是硬币圆周上一点,硬币与数轴相切于原点(A与原点重合).假设硬币的直径为1个单位长度,若将硬币沿数轴正方向滚动一周,点A恰好与数轴上点A’重合,则点A’对应的实数是 .

15.如图所示,用灰白两色正方形瓷砖铺设地面,第6个图案中灰色瓷砖块数为
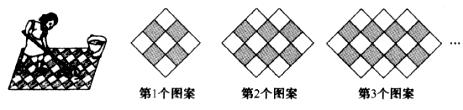
16.在边长为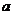 的正方形纸片中剪去一个边长为b的小正方形(
的正方形纸片中剪去一个边长为b的小正方形( )(如图(1)),把余下的部分沿虚线剪开,拼成一个矩形(如图(2)),分别计算这两个图形阴影部分的面积,可以验证的乘法公式是 (用字母表示).
)(如图(1)),把余下的部分沿虚线剪开,拼成一个矩形(如图(2)),分别计算这两个图形阴影部分的面积,可以验证的乘法公式是 (用字母表示).

17.计算机中常用的十六进制是逢16进1的计数制,采用数字0~9和字母A~F共16个计数符号,这些符号与十进制的数的对应关系如下表:
十六进制
0
1
2
3
4
5
6
7
8
9
A
B
C
D
E
F
十进制
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
例如,用十六进制表示;E+F=1D,则A×B= 。
18.甲、乙两人进行羽毛球比赛,甲发出一个十分关键的球,出手点为P,羽毛球飞行的水平距离s(m)与其距地面高度 (m)之间的关系式为
(m)之间的关系式为 ,如图所示,已知球网AB距原点
,如图所示,已知球网AB距原点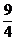 m,设乙的起跳点C的横坐标为
m,设乙的起跳点C的横坐标为 ,若乙原地起跳,因球的高度高于乙扣球的最大高度而导致接球失败,则
,若乙原地起跳,因球的高度高于乙扣球的最大高度而导致接球失败,则 的取值范围是
。
的取值范围是
。

三、解答题(本大题共10小题,共84分,解答应写出文字说明或演算步骤)
19.(本题6分)计算: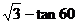 °
°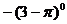
20.(本题6分)课堂上,李老师给大家出了这样一道题:当 时,求代数式
时,求代数式 的值.小明一看,“太复杂了,怎么算呢?”你能帮小明解决这个问题吗?请你写出具体过程.
的值.小明一看,“太复杂了,怎么算呢?”你能帮小明解决这个问题吗?请你写出具体过程.
21.(本题7分)解不等式 ,并将它的解集在图所示的数轴上表示出来。
,并将它的解集在图所示的数轴上表示出来。

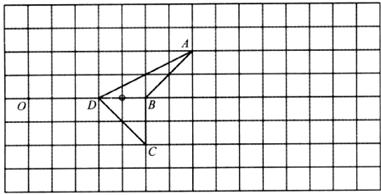
22.(本题8分)如图所示,正方形网格中有一条简笔画“鱼”,请你以点O为位似中心放大,使新图形与原图形的对应线段的比是2:1(不要求写作法).
23.(本题9分)据衢州日报报道:截止

(1)2006年1月衢州市区各区块商品住宅成交均价最高的区块是 ,成交均价的极差为 .
(2)报道数据显示,2006年1月衢州市区六大区块共销售商品住宅493套,那么老城区销售了 套.(精确到个位)
(3)按照1月份的销售速度,现存(即未售)的纳入网上销售的商品住宅(截止
24.(本题10分)已知:如图,在△ABC中,D为AB边上一点,∠A=36°,AC=BC,AC2=AB?AD.
(1)试说明:△ADC和△BDC都是等腰三角形.
(2)若AB=1,求AC的值.
(3)请你构造一个等腰梯形,使得该梯形连同它的两条对角线得到8个等腰三角形.(标明各角的度数)
25.(本题12分)在同一平面直角坐标系中有6个点:A(1,1),B(-3,-1),C(-3,1),D(-2,-2),E(-2,-3),F(0,-4).
(1)画出△ABC的外接圆⊙P,并指出点D与⊙P的位置关系.
(2)若将直线EF沿y轴向上平移,当它经过点D时,设此时的直线为 .
.
①判断直线 与⊙P的位置关系,并说明理由;
与⊙P的位置关系,并说明理由;
②再将直线 绕点D按顺时针方向旋转,当它经过点C时,设此时的直线为
绕点D按顺时针方向旋转,当它经过点C时,设此时的直线为 ,求直线
,求直线 与⊙P的劣弧CD围成的图形的面积(结果保留
与⊙P的劣弧CD围成的图形的面积(结果保留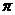 ).
).

26.(本题10分)如图所示,已知等边△ABC,以边BC为直径的半圆与边AB、AC分别交于点D、点E,过点D作DF⊥AC,垂足为点F.
(1)判断DF与⊙O的位置关系,并证明你的结论.
(2)过点F作FH⊥BC,垂足为点H,若等边△ABC的边长为4,求FH的长.(结果保留根号)

27.(本题12分)南博汽车城销售某种型号的汽车,每辆进货价为25万元,市场调研表明:当销售价为29万元时,平均每周能售出8辆,而当销售价每降低0.5万元时,平均每周能多售出4辆.如果设每辆汽车降价 万元,每辆汽车的销售利润为
万元,每辆汽车的销售利润为 万元.(销售利润=销售价-进货价)
万元.(销售利润=销售价-进货价)
(1)求 与
与 的函数关系式,在保证商家不亏本的前提下,写出
的函数关系式,在保证商家不亏本的前提下,写出 的取值范围;
的取值范围;
(2)假设这种汽车平均每周的销售利润为 万元,试写出
万元,试写出 与
与 之间的函数关系式;
之间的函数关系式;
(3)当每辆汽车的定价为多少万元时,平均每周的销售利润最大?最大利润是多少?
28.(本题13分)两个直角边为6的全等的等腰直角三角形Rt△AOB和Rt△CED按图所示的付詈放詈A与C重合,O与E重合.
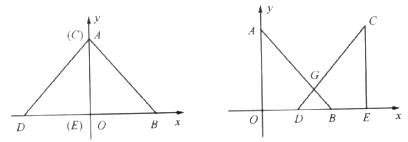
(1)求左图中,A、B、D三点的坐标。
(2)Rt△AOB固定不动,Rt△CED沿 轴以每秒2个单位长的速度向右运动,当D点运动到与B点重合时停止,设运动
轴以每秒2个单位长的速度向右运动,当D点运动到与B点重合时停止,设运动 秒后Rt△CED和Rt△AOB重叠部分面积为y,求
秒后Rt△CED和Rt△AOB重叠部分面积为y,求 与
与 之间的函数关系式.
之间的函数关系式.
(3)当Rt△CED以(2)中的速度和方向运动,运动时间 4秒时Rt△CED运动到如右图所示的位置,求经过A,G,C三点的抛物线的解析式.
4秒时Rt△CED运动到如右图所示的位置,求经过A,G,C三点的抛物线的解析式.
(4)现有一半径为2,圆心P在(3)中的抛物线上运动的动圆,试问⊙P在运动过程中是否存在⊙P与 轴或y轴相切的情况,若存在请求出P的坐标,若不存在请说明理由。
轴或y轴相切的情况,若存在请求出P的坐标,若不存在请说明理由。