2008年江苏省启东中学中考模拟考试 (七)
数学试卷
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷两部分
第Ⅰ卷(选择题,共32分)
一、选择题(本题共10小题;第1~8题每小题3分,第9~10题每小题4分,共32分)下列各题都有代号为A、B、C、D的四个结论供选择,其中只有一个结论是正确的.
1.点P( ,1)在
( )
,1)在
( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.如果 与-2的和为0,那么
与-2的和为0,那么 是
( )
是
( )
A.2 B. C.
C. D.-2
D.-2
3.如图所示,图中阴影部分表示 的取值范围,则下列表示中正确的是 ( )
的取值范围,则下列表示中正确的是 ( )

A. B.
B. ≤
≤ ≤2 D.-3<
≤2 D.-3< <2
<2
4.下列运算正确的是 ( )
A. B.
B.
C. D.
D.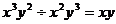
5.其市气象局预报称:明天本市的降水概率为70%,这句话指的是 ( )
A.明天本市70%的时间下雨,30%的时间不下雨
B.明天本市70%的地区下雨,30%的地区不下雨
C.明天本市一定下雨
D.明天本市下雨的可能性是70%
6.将(-sin30°) ,
, ,
, 这三个实数按从小到大的顺序排列,正确的结果是 ( )
这三个实数按从小到大的顺序排列,正确的结果是 ( )
A.(-sin30°) <
< <
< B.(-sin30°)
B.(-sin30°) <
<  <
<
C. <
< < (-sin30°)
< (-sin30°) D.
D. <
< <(-sin30°)
<(-sin30°)
7.如图所示,则△ABC的形状是 ( )

A.锐角三角形 B.钝角三角形 C.直角三角形 D.等腰三角形
8.如图所示,电灯P在横杆AB的正上方,AB在灯光下的影子为CD,AB//CD,AB=2m,CD=5m,点P到CD的距离是3m,则P到AB的距离是 ( )

A.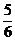 m B.
m B. m C.
m C. m D.
m D.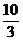 m
m
9.如图所示,将△ABC绕顶点A顺时针旋转60°后,得到△AB'C',且C'为BC的中点, 则C'D:DB'= ( )

A.1:2 B.1:2 C.1:
C.1: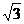 D.1:3
D.1:3
10.如图所示,小李和小陈做转盘游戏,他们同时分别转动一个转盘,当两个转盘都停下来时,指针所指的数字都是奇数的概率是 ( )

A. B.
B. C.
C. D.
D.
第Ⅱ卷(共118分)
二、填空题(本大题共6小题,每小题3分,共18分,把答案填写在题中的横线上.)
11.写出一个有理数和无理数,使它们都是大于-2的负数: .
12.化简: .
.
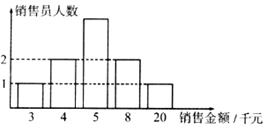
13.如图显示的是绵阳某商场日用品柜台10名售货员4月份完成销售额(单位:千元)的情况,根据统计图,我们可以计算出该柜台的人均销售额为 千元.
14.如图所示,矩形ABCD与圆心在AB上的⊙O交于点G、B、F、E,GB=8cm,AG=1cm,DE=2cm,则EF= cm.

15.三个同学对问题“若方程组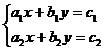 的解是
的解是 ,求方程组
,求方程组 的解。”提出各自的想法。甲说:“这个题目好象条件不够,不能求解”;乙说:“它们的系数有一定的规律,可以试试”;丙说:“能不能把第二个方程组的两个方程的两边都除以5,通过换元替换的方法来解决”。参考他们的讨论,你认为这个题目的解应该是 .
的解。”提出各自的想法。甲说:“这个题目好象条件不够,不能求解”;乙说:“它们的系数有一定的规律,可以试试”;丙说:“能不能把第二个方程组的两个方程的两边都除以5,通过换元替换的方法来解决”。参考他们的讨论,你认为这个题目的解应该是 .
16.古希腊数学家把1,3,6,10,15,21,……,叫做三角形数,根据它的规律,则第100个三角形数与第98个三角形数的差为 .
17.我们常用的数是十进制的数,而计算机程序处理中使用的是只有数码0和1的二进制数.这两者可以相互换算,如将二进制数1101换算成十进制数应为1×23+1×22+0×21+1×20=13,按此方式,则将十进制数25换算成二进制数应为 .
18.如图所示,梯形AOBC的顶点A、C在反比例函数图像上,OA//BC,上底边OA在直线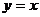 上,下底边BC交
上,下底边BC交 轴于E(2,0),则四边形AOEC的面积为
.
轴于E(2,0),则四边形AOEC的面积为
.

三、解答题(本大题共10小题,共84分,解答应写出文字说明或演算步骤.)
19.(本题满分7分)解不等式组 ,并写出不等式组的正整数解.
,并写出不等式组的正整数解.
20.(本题满分8分)如图所示,在平行四边形ABCD中,将△ABD沿对角线BD对折,得到
△A’BD.
(1)请在图中用直尺和圆规按题意完成作图(不写作法,保留作图痕迹).
(2)证明:∠A’=∠C.

21.(本题8分)探究下表中的奥秘,并完成填空:
一元二次方程
两个根
二次三项式因式分解

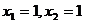







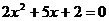



 ,
,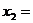
 )
)
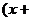 )
)
将你发现的结论一般化,开写出来.
22.(本题满分9分)某块试验田里的农作物每天的需水量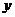 (kg)与生长时间
(kg)与生长时间 (天)之间的关系如折线图所示.这些农作物在第10天、第30天的需水量分别为2000kg、3000kg,在第40天后每天的需水量比前一天增加100kg.
(天)之间的关系如折线图所示.这些农作物在第10天、第30天的需水量分别为2000kg、3000kg,在第40天后每天的需水量比前一天增加100kg.
(1)分别求出 ≤40和
≤40和 ≥40时
≥40时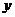 与
与 之间的关系式.
之间的关系式.
(2)如果这些农作物每天的需水量大于或等于4000kg时需要进行人工灌溉,那么应从第几天开始进行人工灌溉?
23.(本题9分)三个生产日光灯管的厂家在广告中宣称,他们生产的日光灯管在正常情况下,灯管的使用寿命为12个月.工商部门为了检查他们宣传的真实性,从三个厂家各柚取11只日光灯管进行检测,灯管的使用寿命(单位:月)如下:
甲厂
7
8
9
9
9
11
13
14
16
17
19
乙厂
7
7
9
9
10
10
12
12
12
13
14
丙厂
7
7
8
8
8
12
13
14
15
16
17
试问:
(1)这三个厂家的广告,分别利用了统计中的哪一个特征数(平均数、中位数、众数)进行宣传?
(2)如果三种产品的售价一样,作为顾客的你选购哪个厂家的产品?请说明理由.
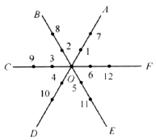
24.(本题9分)如图,平面内有公共端点的六条射线OA,OB,OC,OD,OE,OF,从射线OA开始按逆时针方向依次在射线上写出数字1,2,3,4,5,6,7,….
(1)“17”在射线 上.
(2)请任意写出三条射线上数字的排列规律.
(3)“2007”在哪条射线上?
25.(本题满分9分)汪老师要装修自己带阁楼的新居(图为新居剖面图),在建造客厅到阁楼的楼梯AC时,为避免上楼时墙角F碰头,设计墙角F到楼梯的竖直距离FG为1.75m.他量得客厅高AB=2.8m,楼梯洞口宽AF=2m,阁楼阳台宽EF=3m.请你帮助汪老师解决下列问题:
(1)要使墙角F到楼梯的竖直距离FG为1.75m,楼梯底端C到墙角D的距离CD是多少米?
(2)在(1)的条件下,为保证上楼时的舒适感,楼梯的每个台阶高度小于20cm,每个台阶宽要大于20cm,问汪老师应该将楼梯建几个台阶?为什么?

26.(本题满分10分)在某次数字变换游戏中,我们把整数0,1,2,…,100称为“旧数”,游戏的变换规则是:将旧数先平方,再除以100,所得到的数称为“新数”.
(1)请把旧数80和26按照上述规则变换为新数.
(2)经过上述规则变换后,我们发现许多旧数变小了.有人断言:“按照上述变换规则,所有的‘新数’都不等于它的‘旧数’”,你认为这种说法对吗?若不对,请求出所有不符合这一说法的旧数.
(3)请求出按照上述规则变换后减小得最多的旧数(要写出解答过程).
27.(本题l2分)在△ABC中,AB=AC,CG⊥BA交BA的延长线于点G.一等腰直角三角尺按如图1所示的位置摆放,该三角尺的直角顶点为F,一条直角边与AC边在一条直线上,另一条直角边恰好经过点B.
(1)在图1中请你通过观察、测量BF与CG的长度,猜想并写出BF与CG满足的数量关系,然后证明你的猜想.
(2)当三角尺沿AC方向平移到图2所示的位置时,一条直角边仍与AC边在同一直线E,另一条直角边交BC边于点D,过点D作DE⊥BA于点E.此时请你通过观察、测量DE、DF与CG的长度,猜想并写出DE+DF与CG之间满足的数量关系,然后证明你的猜想.
(3)当三角尺在(2)的基础上沿AC方向继续平移到图1所示的位置(点F在线段AC上,且点F与点C不重合)时,(2)中的猜想是否仍然成立?(不用说明理由)

28.(本题满分13分)如图所示,已知开口向上的抛物线 与
与 轴交于
轴交于
A(-3,0)、B(1,0)两点,与y轴交于C点,∠ACB不小于90°.
(1)求点C的坐标(用含 的代数式表示);
的代数式表示);
(2)求系数 的取值范围;
的取值范围;
(3)设抛物线的顶点为D,求△BCD中CD边上的高 的最大值.
的最大值.
