2008年江苏省启东中学中考模拟试卷(三)
数学试卷
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷两部分
第Ⅰ卷(选择题,共32分)
一、选择题(本题共10小题;第1―8题每小题3分,第9―10题每小题4分,共32分)
1.
A. m B.
m B. m
m
C. m D.
m D. m
m
2.① ;②
;②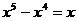 ;③
;③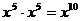 ;④
;④ ;⑤
;⑤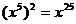 。其中结果正确的是
。其中结果正确的是
A.①②④ B.②④ C.③ D.④⑤
3.下列图形中,既是轴对称图形又是中心对称图形的是
A.等腰三角形 B.直角三角形 C.平行四边形 D.菱形
4.棱长是

A.
5.函数 中,自变量
中,自变量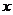 的取值范围是
的取值范围是
A. B.
B. C.
C.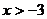 D.
D.
6.图2所示的平面图形中,是正方体的平面展开图的是

7.小明把自己一周的支出情况,用如图3所示的统计图来表示,下面说法正确的是
A.从图中可以直接看出具体消费数额
B.从图中可以直接看出总消费数额
C.从图中可以直接看出各项消费数额占总消费额的百分比
D.从图中可以直接看出各项消费数额在一周中的具体变化情况

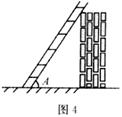
8.如图4所示,梯子与地面的夹角为A,关于∠A的三角函数值与梯子的倾斜程度之间,叙述正确的是
A.sinA的值越小,梯子越陡
B.cosA的值越小,梯子越陡
C.tanA的值越小,梯子越陡
D.梯子的陡缓程度与∠A的函数值无关
9.如图5所示,一个小球从A点沿制定的轨道下落,在每个交叉口都有向左或向右两种机会均等的结果,小球最终到达H点的概率是
A.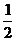 B.
B.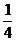 C.
C.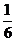 D.
D.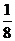


10.如图6,一只蚂蚁以均匀的速度沿台阶A1→A2→A3→A4→A5爬行,那么蚂蚁爬行的高度h随时间t变化的图像大致是

第Ⅱ卷(共118分)
请把最后结果填在题中横线上。
二、填空题(本题共8小题;每小题3分,共18分)
11.分解因式: 。
。
12.如图7所示的五角星绕中心点旋转一定的角度后能与自身完全重合,则其旋转的角度至少为 。

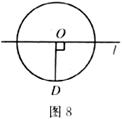
13.如图8所示,⊙O的半径OD为 ,垂足为O,则直线
,垂足为O,则直线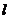 沿射线OD方向平移
cm时与⊙O相切。
沿射线OD方向平移
cm时与⊙O相切。
14.小明的身高是
15.已知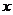 是一元二次方程
是一元二次方程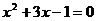 的实数根,那么代数式
的实数根,那么代数式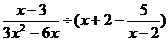 的值为
。
的值为
。
16.将圆柱形纸筒沿母线AB剪开铺平,得到一个矩形(如图9),如果将这个纸筒沿线路B→M→A剪开铺平,得到的图形是 。


17.如图10,房间里有一只老鼠,门外蹲着一只小猫,如果每块正方形地砖的边长为
18.如图11,在平面直角坐标系中,有若干个整数点,其顺序按图中“→”方向排列,如(1,0),(2,0),(2,1),(3,2),(3,1),(3,0)…根据这个规律探索可得,第100个点的坐标为 。

19.(本小题12分)
(1)计算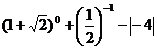
(2)解方程
20.(本小题7分)解不等式组,并把解集在数轴上表示出来。
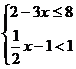
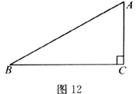
21.(本题7分)如图12所示,要在一块形状为直角三角形的铁皮上裁出一个半圆形的铁皮,需先在这块铁皮上画出半圆,使它的圆心在AC上,且与AB、BC都相切,请你用直尺和圆规画出来(保留作图痕迹,写出作法,不要求证明和讨论)。
22.(本题7分)在某旅游景区上山的一条小路上,有一些断断续续的台阶,图13是其中的甲、乙段台阶路的示意图。请你用所学过的有关统计知识(平均数、中位数、方差和极差)回答下列问题:
(1)两段台阶路有哪些相同点和不同点?
(2)哪段台阶路走起来更舒服?为什么?
(3)为方便游客行走,需要重新整修上山的小路.对于这两段台阶路,在台阶数不变的情况下,请你提出合理的整修建议。

23.(本题9分)市政公司为绿化一段沿江风光带,计划购买甲、乙两种树苗共500株,甲种树苗每株50元,乙种树苗每株80元。有关统计表明:甲、乙两种树苗的成活率分别为90%和95%。
(1)若购买树苗共用了28000元,求甲、乙两种树苗各多少株?
(2)若购买树苗的钱不超过34000元,应如何选购树苗?
(3)若希望这批树苗的成活率不低于92%,且购买树苗的费用最低,应如何选购树苗?
五、解答题(本题共2小题;共16分)
24.(本小题8分)定理证明:“等腰梯形的两条对角线相等”。
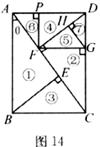
25.(本小题8分)我们知道,“直角三角形斜边上的高线将三角形分成两个与原三角形相似的直角三角形”。用这一方法,将矩形ABCD分割成大小不同的七个相似直角三角形,按从大到小的顺序编号为①~⑦(如图14),从而割成一副“三角七巧板”。已知线段AB=1, 。
。
(1)请用 的三角函数表示线段BE的长为
;
的三角函数表示线段BE的长为
;
(2)图中与线段BE相等的线段是 ;
(3)仔细观察图形,求出⑦中最短的直角边DH的长(用 的三角函数表示)。
的三角函数表示)。
26.(本小题10分)在日常生活中,我们经常看到一些窗户上安装着遮阳篷,如图
(1)遮阳篷BCD怎样设计,才能正好在冬天正午太阳最低时光线最大限度地射入室内,而夏天正午太阳最高时光线刚好不射入室内?请在图
(2)已知AB=

27.(本小题12分)如图16所示,正方形OCED与扇形OAB有公共顶点O,分别以OA、OB所在直线为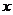 轴、
轴、 轴建立平面直角坐标系.正方形两个顶点C、D分别在
轴建立平面直角坐标系.正方形两个顶点C、D分别在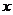 轴、
轴、 轴正半轴上移动.设OC=
轴正半轴上移动.设OC=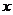 ,OA=3。
,OA=3。
(1)当 时,正方形与扇形不重合的面积是
;此时,直线CD对应的函数关系式是
。
时,正方形与扇形不重合的面积是
;此时,直线CD对应的函数关系式是
。
(2)当直线CD与扇形OAB相切时.求直线CD对应的函数关系式;
(3)当正方形有顶点恰好落在AB上时,求正方形与扇形不重合的面积。

28.(本题14分)在平面直角坐标系 中,已知二次函数
中,已知二次函数 的图像与
的图像与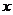 轴交于A、B两点(点A在点B的左边),与
轴交于A、B两点(点A在点B的左边),与 轴交于点C,其顶点的横坐标为1,且过点(2,3)和(-3,-12)。
轴交于点C,其顶点的横坐标为1,且过点(2,3)和(-3,-12)。
(1)求此二次函数的表达式。
(2)若直线 与线段BC交于点D(不与点B,C重合),则是否存在这样的直线
与线段BC交于点D(不与点B,C重合),则是否存在这样的直线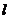 ,使得以B、O、D为顶点的三角形与△BAC相似?若存在,求出该直线的函数表达式及点D的坐标;若不存在,请说明理由。
,使得以B、O、D为顶点的三角形与△BAC相似?若存在,求出该直线的函数表达式及点D的坐标;若不存在,请说明理由。
(3)若点P是位于该二次函数对称轴右边图像上不与顶点重合的任意一点,试比较锐角∠ POC与∠ACO的大小(不必证明),并写出此时点P的横坐标却的取值范围。
