2008年山东省青岛市初级中学学业水平考试
数学试题
(考试时间:120分钟;满分120分)
一、选择题(本题满分21分,共有7道小题,每小题3分)
1.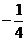 的相反数等于( )
的相反数等于( )
A.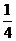 B.
B.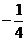 C.
C.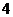 D.
D.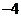
2.下列图形中,轴对称图形的个数是( )

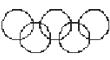


A.1 B.
3.已知⊙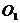 和⊙
和⊙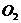 的半径分别为3cm和2cm,圆心距
的半径分别为3cm和2cm,圆心距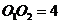 cm,则两圆的位置关系是( )
cm,则两圆的位置关系是( )
A.相切 B.内含 C.外离 D.相交
4.某几何体的三种视图如下图所示,则该几何体可能是( )
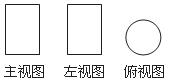
A.圆锥体 B.球体 C.长方体 D.圆柱体
5.一个口袋中有3个黑球和若干个白球,在不允许将球倒出来数的前提下,小明为估计其中的白球数,采用了如下的方法:从口袋中随机摸出一球,记下颜色,然后把它放回口袋中,摇匀后再随机摸出一球,记下颜色, ,不断重复上述过程.小明共摸了100次,其中20次摸到黑球.根据上述数据,小明可估计口袋中的白球大约有( )
,不断重复上述过程.小明共摸了100次,其中20次摸到黑球.根据上述数据,小明可估计口袋中的白球大约有( )
A.18个 B.15个 C.12个 D.10个
6.如果点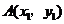 和点
和点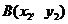 是直线
是直线 上的两点,且当
上的两点,且当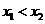 时,
时, ,那么函数
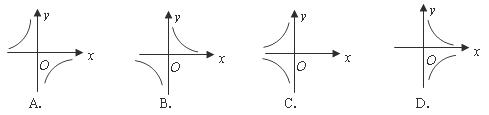
,那么函数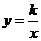 的图象大致是( )
的图象大致是( )
7.如图,把图①中的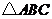 经过一定的变换得到图②中的
经过一定的变换得到图②中的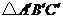 ,如果图①中
,如果图①中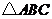 上点
上点 的坐标为
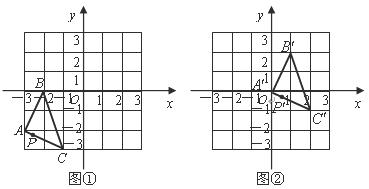
的坐标为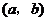 ,那么这个点在图②中的对应点
,那么这个点在图②中的对应点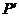 的坐标为( )
的坐标为( )
A.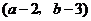 B.
B. C.
C. D.
D.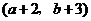
二、填空题(本题满分21分,共有7道小题,每小题3分)
8.计算: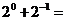 .
.
9.化简: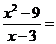 .
.
10.如图,在矩形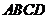 中,对角线
中,对角线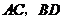 相交于点
相交于点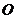 ,若
,若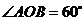 ,
,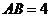 cm,则
cm,则 的长为
cm.
的长为
cm.

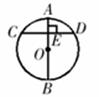
11.如图,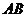 是⊙
是⊙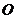 的直径,弦
的直径,弦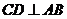 于
于 ,如果
,如果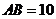 ,
,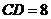 ,那么
,那么 的长为
.
的长为
.
12.为了帮助四川地震灾区重建家园,某学校号召师生自愿捐款.第一次捐款总额为20000元,第二次捐款总额为56000元,已知第二次捐款人数是第一次的2倍,而且人均捐款额比第一次多20元.求第一次捐款的人数是多少?若设第一次捐款的人数为 ,则根据题意可列方程为
.
,则根据题意可列方程为
.
测试项目
测试成绩

面试
90
95
综合知识测试
85
80
13.某市广播电视局欲招聘播音员一名,对 两名候选人进行了两项素质测试,两人的两项测试成绩如下表所示.根据实际需要,广播电视局将面试、综合知识测试的得分按
两名候选人进行了两项素质测试,两人的两项测试成绩如下表所示.根据实际需要,广播电视局将面试、综合知识测试的得分按 的比例计算两人的总成绩,那么
(填
的比例计算两人的总成绩,那么
(填 或
或 )将被录用.
)将被录用.
14.如图是一个用来盛爆米花的圆锥形纸杯,纸杯开口圆的直径 长为10cm.母线
长为10cm.母线 长为10cm.在母线
长为10cm.在母线 上的点
上的点 处有一块爆米花残渣,且
处有一块爆米花残渣,且 cm,一只蚂蚁从杯口的点
cm,一只蚂蚁从杯口的点 处沿圆锥表面爬行到
处沿圆锥表面爬行到 点.则此蚂蚁爬行的最短距离为
cm.
点.则此蚂蚁爬行的最短距离为
cm.

用圆规、直尺作图,不写作法,但要保留作图痕迹.
三、作图题(本题满分6分)
15.如图,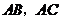 表示两条相交的公路,现要在
表示两条相交的公路,现要在 的内部建一个物流中心.设计时要求该物流中心到两条公路的距离相等,且到公路交叉处
的内部建一个物流中心.设计时要求该物流中心到两条公路的距离相等,且到公路交叉处 点的距离为1000米.
点的距离为1000米.
(1)若要以 的比例尺画设计图,求物流中心到公路交叉处
的比例尺画设计图,求物流中心到公路交叉处 点的图上距离;
点的图上距离;
(2)在图中画出物流中心的位置 .
.
解:(1)
(2)

四、解答题(本题满分72分,共有9道小题)
16.(本小题满分6分)
用配方法解一元二次方程: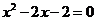 .
.
17.(本小题满分6分)
某市为调查学生的视力变化情况,从全市九年级学生中抽取了部分学生,统计了每个人连续三年视力检查的结果,并将所得数据处理后,制成折线统计图和扇形统计图如下:
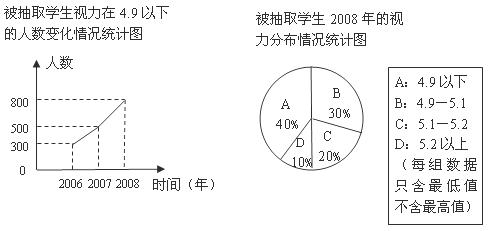
解答下列问题:
(1)该市共抽取了多少名九年级学生?
(2)若该市共有8万名九年级学生,请你估计该市九年级视力不良(4.9以下)的学生大约有多少人?
(3)根据统计图提供的信息,谈谈自己的感想(不超过30字).
18.(本小题满分6分)
小明和小刚用如图所示的两个转盘做配紫色游戏,游戏规则是:分别旋转两个转盘,若其中一个转盘转出了红色,另一个转出了蓝色,则可以配成紫色.此时小刚得1分,否则小明得1分.
这个游戏对双方公平吗?请说明理由.若你认为不公平,如何修改规则才能使游戏对双方公平?

19.(本小题满分6分)
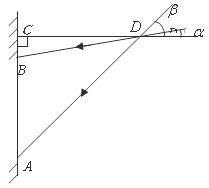
在一次课题学习课上,同学们为教室窗户设计一个遮阳蓬,小明同学绘制的设计图如图所示,其中,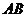 表示窗户,且
表示窗户,且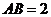 米,
米,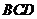 表示直角遮阳蓬,已知当地一年中在午时的太阳光与水平线
表示直角遮阳蓬,已知当地一年中在午时的太阳光与水平线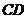 的最小夹角
的最小夹角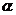 为
为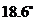 ,最大夹角
,最大夹角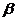 为
为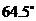 .
.
请你根据以上数据,帮助小明同学计算出遮阳蓬中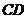 的长是多少米?(结果保留两个有效数字)
的长是多少米?(结果保留两个有效数字)
(参考数据: ,
,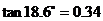 ,
,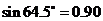 ,
,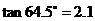 )
)
20.(本小题满分8分)
2008年8月,北京奥运会帆船比赛将在青岛国际帆船中心举行.观看帆船比赛的船票分为两种:A种船票600元/张,B种船票120元/张.某旅行社要为一个旅行团代购部分船票,在购票费不超过5000元的情况下,购买A,B两种船票共15张,要求A种船票的数量不少于B种船票数量的一半.若设购买A种船票 张,请你解答下列问题:
张,请你解答下列问题:
(1)共有几种符合题意的购票方案?写出解答过程;
(2)根据计算判断:哪种购票方案更省钱?
21.(本小题满分8分)
已知:如图,在正方形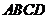 中,
中,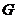 是
是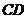 上一点,延长
上一点,延长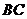 到
到 ,使
,使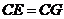 ,连接
,连接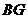 并延长交
并延长交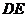 于
于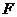 .
.
(1)求证: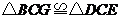 ;
;
(2)将 绕点
绕点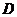 顺时针旋转
顺时针旋转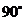 得到
得到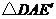 ,判断四边形
,判断四边形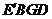 是什么特殊四边形?并说明理由.
是什么特殊四边形?并说明理由.
22.(本小题满分10分)
某服装公司试销一种成本为每件50元的T恤衫,规定试销时的销售单价不低于成本价,又不高于每件70元,试销中销售量 (件)与销售单价
(件)与销售单价 (元)的关系可以近似的看作一次函数(如图).
(元)的关系可以近似的看作一次函数(如图).
(1)求 与
与 之间的函数关系式;
之间的函数关系式;
(2)设公司获得的总利润(总利润 总销售额
总销售额 总成本)为
总成本)为 元,求
元,求 与
与 之间的函数关系式,并写出自变量
之间的函数关系式,并写出自变量 的取值范围;根据题意判断:当
的取值范围;根据题意判断:当 取何值时,
取何值时, 的值最大?最大值是多少?
的值最大?最大值是多少?

23.(本小题满分10分)
实际问题:某学校共有18个教学班,每班的学生数都是40人.为了解学生课余时间上网情况,学校打算做一次抽样调查,如果要确保全校抽取出来的学生中至少有10人在同一班级,那么全校最少需抽取多少名学生?
建立模型:为解决上面的“实际问题”,我们先建立并研究下面从口袋中摸球的数学模型:
在不透明的口袋中装有红、黄、白三种颜色的小球各20个(除颜色外完全相同),现要确保从口袋中随机摸出的小球至少有10个是同色的,则最少需摸出多少个小球?
为了找到解决问题的办法,我们可把上述问题简单化:
(1)我们首先考虑最简单的情况:即要确保从口袋中摸出的小球至少有2个是同色的,则最少需摸出多少个小球?
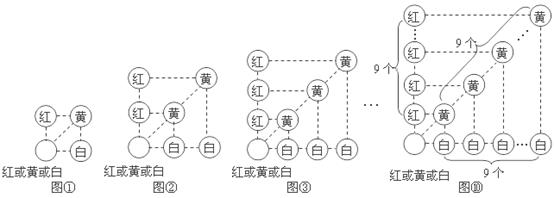
假若从袋中随机摸出3个小球,它们的颜色可能会出现多种情况,其中最不利的情况就是它们的颜色各不相同,那么只需再从袋中摸出1个小球就可确保至少有2个小球同色,即最少需摸出小球的个数是: (如图①);
(如图①);
(2)若要确保从口袋中摸出的小球至少有3个是同色的呢?
我们只需在(1)的基础上,再从袋中摸出3个小球,就可确保至少有3个小球同色,即最少需摸出小球的个数是: (如图②)
(如图②)
(3)若要确保从口袋中摸出的小球至少有4个是同色的呢?
我们只需在(2)的基础上,再从袋中摸出3个小球,就可确保至少有4个小球同色,即最少需摸出小球的个数是: (如图③):
(如图③):

(10)若要确保从口袋中摸出的小球至少有10个是同色的呢?
我们只需在(9)的基础上,再从袋中摸出3个小球,就可确保至少有10个小球同色,即最少需摸出小球的个数是: (如图⑩)
(如图⑩)
模型拓展一:在不透明的口袋中装有红、黄、白、蓝、绿五种颜色的小球各20分(除颜色外完全相同),现从袋中随机摸球:
(1)若要确保摸出的小球至少有2个同色,则最少需摸出小球的个数是 ;
(2)若要确保摸出的小球至少有10个同色,则最少需摸出小球的个数是 ;
(3)若要确保摸出的小球至少有 个同色(
个同色( ),则最少需摸出小球的个数是 .
),则最少需摸出小球的个数是 .
模型拓展二:在不透明口袋中装有 种颜色的小球各20个(除颜色外完全相同),现从袋中随机摸球:
种颜色的小球各20个(除颜色外完全相同),现从袋中随机摸球:
(1)若要确保摸出的小球至少有2个同色,则最少需摸出小球的个数是 .
(2)若要确保摸出的小球至少有 个同色(
个同色( ),则最少需摸出小球的个数是 .
),则最少需摸出小球的个数是 .
问题解决:(1)请把本题中的“实际问题”转化为一个从口袋中摸球的数学模型;
(2)根据(1)中建立的数学模型,求出全校最少需抽取多少名学生.
24.(本小题满分12分)
已知:如图①,在 中,
中, ,
, ,
, ,点
,点 由
由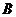 出发沿
出发沿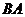 方向向点
方向向点 匀速运动,速度为1cm/s;点
匀速运动,速度为1cm/s;点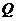 由
由 出发沿
出发沿 方向向点
方向向点 匀速运动,速度为2cm/s;连接
匀速运动,速度为2cm/s;连接 .若设运动的时间为
.若设运动的时间为 (
( ),解答下列问题:
),解答下列问题:
(1)当 为何值时,
为何值时,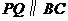 ?
?
(2)设 的面积为
的面积为 (
( ),求
),求 与
与 之间的函数关系式;
之间的函数关系式;
(3)是否存在某一时刻 ,使线段
,使线段 恰好把
恰好把 的周长和面积同时平分?若存在,求出此时
的周长和面积同时平分?若存在,求出此时 的值;若不存在,说明理由;
的值;若不存在,说明理由;
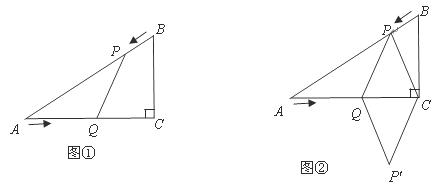
(4)如图②,连接 ,并把
,并把 沿
沿 翻折,得到四边形
翻折,得到四边形 ,那么是否存在某一时刻
,那么是否存在某一时刻 ,使四边形
,使四边形 为菱形?若存在,求出此时菱形的边长;若不存在,说明理由.
为菱形?若存在,求出此时菱形的边长;若不存在,说明理由.