江苏通州市高三第四次统一检测
数学试题
第Ⅰ部分必考内容
(命题单位:通州中学 满分160分,答卷时间120分钟)
一、填空题:本大题共14小题,每小题5分,共70分.不需写出解答过程,请把答案填写在答题纸相应位置上.
1.对于命题p: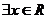 ,使得x 2+ x +1 < 0.则
,使得x 2+ x +1 < 0.则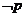 为:_________.
为:_________.
2.复数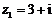 ,
,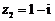 ,则复数
,则复数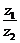 在复平面内对应的点位于第_______象限.
在复平面内对应的点位于第_______象限.
3.“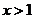 ”是“
”是“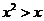 ”的
条件.
”的
条件.
4.一个靶子上有10个同心圆,半径依次为1、2、……、10,击中由内至外的区域的成绩依次为10、9、……、1环,则不考虑技术因素,射击一次,在有成绩的情况下成绩为10环的概率为 .
5.设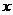 、
、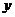 满足条件
满足条件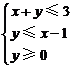 ,则
,则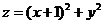 的最小值 .
的最小值 .
6.如果执行下面的程序框图,那么输出的
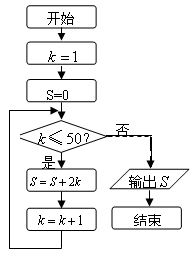
7.△ABC中,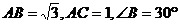 ,则△ABC的面积等于_________.
,则△ABC的面积等于_________.
8.给出下列命题:
①变量 y与x之间的相关系数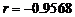 ,查表到相关系数的临界值为
,查表到相关系数的临界值为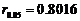 ,则变量
y与x之间具有线性关系;
,则变量
y与x之间具有线性关系;
② 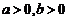 则不等式
则不等式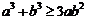 恒成立;
恒成立;
③ 对于函数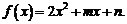 若
若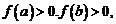 则函数在
则函数在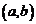 内至多有一个零点;
内至多有一个零点;
④ 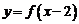 与
与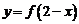 的图象关于
的图象关于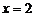 对称.
对称.
其中所有正确命题的序号是__________.
10.已知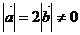 ,且关于x的函数f(x)=
,且关于x的函数f(x)=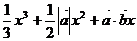 在R上有极值,则
在R上有极值,则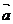 与
与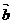 的夹角范围为_______.
的夹角范围为_______.
11.已知数列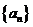 为等差数列,且
为等差数列,且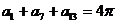 ,则
,则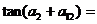 ________.
________.
12.函数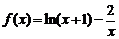 的零点所在的区间是(n,n+1),则正整数n=______.
的零点所在的区间是(n,n+1),则正整数n=______.
13.四棱锥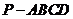 的顶点P在底面ABCD中的投影恰好是A,其三视图如图:
的顶点P在底面ABCD中的投影恰好是A,其三视图如图:
则四棱锥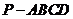 的表面积为 .
的表面积为 .

14.已知点P是抛物线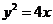 上的动点,点P在y轴上的射影是M,点A的坐标是(4,a),则当
上的动点,点P在y轴上的射影是M,点A的坐标是(4,a),则当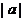
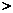 4时,
4时,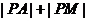 的最小值是
.
的最小值是
.
二、解答题:本大题共6小题,共90分.解答时应写出文字说明、证明过程或演算步骤
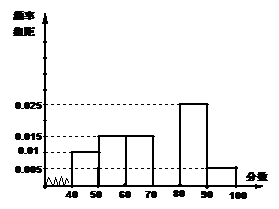 15.(本题满分12分)某校从参加高一年级期末考试的学生中抽出60名学生,将其成绩(是不小于40不大于100的整数)分成六段
15.(本题满分12分)某校从参加高一年级期末考试的学生中抽出60名学生,将其成绩(是不小于40不大于100的整数)分成六段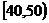 ,
,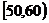 …
… 后
后
(1)求第四小组的频率,并补全这个画出如下部分频率分布直方图.
(2) 观察频率分布直方图图形的 信息,估计这次考试的及格率(60分及以上为及格)和平均分.
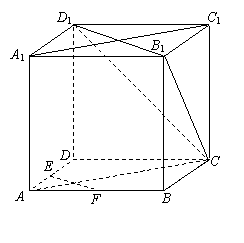
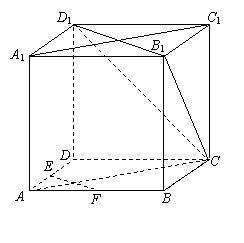 16. (本题满分13分)如图,在正方体ABCD-A1B
16. (本题满分13分)如图,在正方体ABCD-A1B
(1)求证:EF∥平面CB1D1;
(2)求证:平面CAA
17.(本题满分15分)在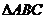 中,
中,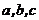 分别是角A、B、C的对边,
分别是角A、B、C的对边, 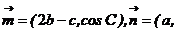
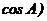 ,且
,且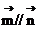 .
.
(1)求角A的大小;
(2)求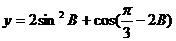 的值域.
的值域.
18.(本题满分15分)椭圆C的中心为坐标原点O,焦点在y轴上,离心率e = ,椭圆上的点到焦点的最短距离为1-, 直线l与y轴交于点P(0,m),与椭圆C交于相异两点A、B,且 .
.
(1)求椭圆方程;
(2)若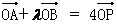 ,求m的取值范围.
,求m的取值范围.
19.(本题满分16分)已知数列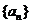 的首项
的首项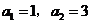 ,前
,前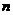 项和为
项和为 ,且
,且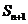 、
、 、
、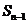 (n ≥2)分别是直线
(n ≥2)分别是直线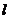 上的点A、B、C的横坐标,
上的点A、B、C的横坐标,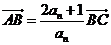 ,设
,设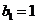 ,
,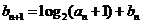 .
.
⑴ 判断数列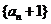 是否为等比数列,并证明你的结论;
是否为等比数列,并证明你的结论;
⑵ 设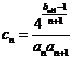 ,证明:
,证明: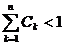 .
.
20.对于函数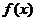 ,若存在
,若存在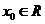 ,使
,使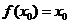 成立,则称
成立,则称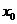 为
为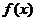 的不动点。如果函数
的不动点。如果函数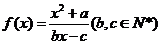 有且仅有两个不动点
有且仅有两个不动点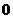 、
、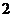 ,且
,且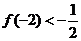 。
。
(1)试求函数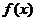 的单调区间;
的单调区间;
(2)点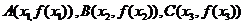 从左到右依次是函数
从左到右依次是函数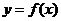 图象上三点,其中
图象上三点,其中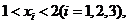 求证:ㄓ
求证:ㄓ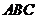 是钝角三角形.
是钝角三角形.
第Ⅱ部分 加试内容
(命题单位:通州中学 满分40分,答卷时间30分钟)
一.必答题:本大题共2小题,解答时应写出文字说明、证明过程或演算步骤.
1.(本小题满分10分)一个盒子装有六张卡片,上面分别写着如下六个定义域为R的函数:f1(x)=x,f2(x)=x2,f3(x)=x3,f4(x)=sinx,f5(x)=cosx,f6(x)=2.
(1)现从盒子中任取两张卡片,将卡片上的函数相加得一个新函数,求所得函数是奇函数的概率;
(2)现从盒子中进行逐一抽取卡片,且每次取出后均不放回,若取到一张记有偶函数的卡片则停止抽取,否则继续进行,求抽取次数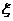 的分布列和数学期望.
的分布列和数学期望.
2.(本小题满分10分)已知数列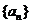 满足
满足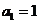 ,且
,且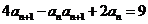 (
(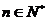 )
)
(1)求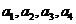 的值;
的值;
(2)由(1)猜想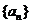 的通项公式,并给出证明.
的通项公式,并给出证明.
二、选答题:本大题共4小题,请从这4题中选做2小题,如果多做,则按所做的前两题记分.每小题10分,共20分.解答时应写出文字说明、证明过程或演算步骤.
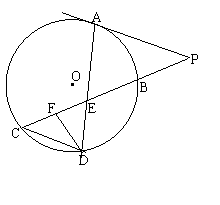 3.(几何证明选讲)(本小题满分10分)如图所示,已知PA与⊙O相切,A为切点,PBC为割线,,弦CD∥AP,AD、BC相交于E点,F为CE上一点,且DE2=EF?EC.
3.(几何证明选讲)(本小题满分10分)如图所示,已知PA与⊙O相切,A为切点,PBC为割线,,弦CD∥AP,AD、BC相交于E点,F为CE上一点,且DE2=EF?EC.
(1)求证:ÐP=ÐEDF;
(2)求证:CE?EB=EF?EP.
4.(矩阵与变换)
(本小题满分10分)设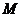 是把坐标平面上的点的横坐标伸长到
是把坐标平面上的点的横坐标伸长到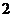 倍,纵坐标伸长到
倍,纵坐标伸长到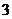 倍的伸压变换. 求逆矩阵
倍的伸压变换. 求逆矩阵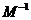 以及椭圆
以及椭圆 在
在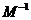 的作用下的新曲线的方程.
的作用下的新曲线的方程.
5.(坐标系与参数方程)
(本小题满分10分)已知直线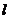 经过点
经过点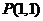 ,倾斜角
,倾斜角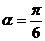 ,
,
(1)写出直线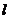 的参数方程;
的参数方程;
(2)设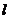 与圆
与圆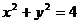 相交与两点
相交与两点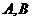 ,求点
,求点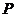 到
到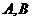 两点的距离之积.
两点的距离之积.
6.(不等式选讲)
(本小题满分10分)设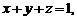 求
求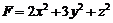 的最大值.
的最大值.
江苏通州市高三第四次统一检测
数学试题(答卷)
一、填空题:本大题共14小题,每小题5分,共70分.不需写出解答过程,请把答案直接填写在相应位置上.
1.________________2._____________3._______________ 4.____________
5._______________6.______________7._______________ 8.____________
9._______________ 10.____________ 11.______________ 12.___________
13._________________ 14._______________
二、解答题:本大题共6小题,共90分.解答时应写出文字说明、证明过程或演算步骤
 15.(本题满分12分)
15.(本题满分12分)
16. (本题满分13分)
17.(本题满分15分)
18.(本题满分16分)
19.(本题满分16分)
20.(本题满分18分)
江苏通州市高三第三次统一检测数学答卷
第Ⅱ部分 加试内容
一.必答题:本大题共2小题,解答时应写出文字说明、证明过程或演算步骤.
1.(本小题满分10分)
2.(本小题满分10分)
选答题1,你所选择的题号是 .
解:
选答题2,你所选择的题号是 .
解:
一、填空题:
1.
 ,均有x 2+ x +1≥0 2.第一象限 3.充分而不必要条件 4. 0.01
,均有x 2+ x +1≥0 2.第一象限 3.充分而不必要条件 4. 0.01
5. 4 6. 2550 7.  8.①④ 9. R(S1+S2+S3+S4)
8.①④ 9. R(S1+S2+S3+S4)
10.
 ,11.
,11.  12.1
13.
12.1
13.
 14.
14. 
二、解答题:
15.(Ⅰ)因为各组的频率和等于1,故第四组的频率:

 3′
3′
直方图如右所示 6′



 (Ⅱ)依题意,60及以上的分数所在的第三、四、五、六组,频率和为
(Ⅱ)依题意,60及以上的分数所在的第三、四、五、六组,频率和为  所以,抽样学生成绩的合格率是
所以,抽样学生成绩的合格率是 %.. 9 ′
%.. 9 ′
利用组中值估算抽样学生的平均分

=
 =71
=71
估计这次考试的平均分是71分 12′
16.(1)证明:连结BD.
在长方体 中,对角线
中,对角线 .
.
又 E、F为棱AD、AB的中点,
E、F为棱AD、AB的中点,
 .
.
 .
.
又B1D1平面 ,
, 平面
平面 ,
,
 EF∥平面CB1D1. 6′
EF∥平面CB1D1. 6′
(2) 在长方体
在长方体 中,AA1⊥平面A1B
中,AA1⊥平面A1B
 AA1⊥B1D1.
AA1⊥B1D1.
又 在正方形A1B
在正方形A1B
 B1D1⊥平面CAA
B1D1⊥平面CAA
又 B1D1平面CB1D1,
B1D1平面CB1D1,
 平面CAA
平面CAA
17. (1)由 得
得 4′
4′
由正弦定理得



 6′
6′
 8′
8′
(2)
= 10′
10′
= 12′
12′
由(1)得


 15′
15′
18.(1)设C:+=1(a>b>0),设c>0,c2=a2-b2,由条件知a-c=,=,
∴a=1,b=c=,
故C的方程为:y2+=1 5′
(2)由=λ,
∴λ+1=4,λ=3 或O点与P点重合= 7′
当O点与P点重合=时,m=0
当λ=3时,直线l与y轴相交,则斜率存在。
设l与椭圆C交点为A(x1,y1),B(x2,y2)
得(k2+2)x2+2kmx+(m2-1)=0
Δ=(
x1+x2=, x1x2= 11′
∵=3 ∴-x1=3x2 ∴
消去x2,得3(x1+x2)2+4x1x2=0,∴3()2+4=0
整理得4k
m2=时,上式不成立;m2≠时,k2=,
因λ=3 ∴k≠0 ∴k2=>0,∴-1<m<- 或 <m<1
容易验证k2>
即所求m的取值范围为(-1,-)∪(,1)∪{0} 16′
19. ⑴由题意得 4′
4′

 (n≥2),
(n≥2),
又∵ ,
,
 数列
数列 是以
是以 为首项,以2为公比的等比数列。 8′
为首项,以2为公比的等比数列。 8′
[则

 (
( )]
)]
⑵由 及
及 得
得

 ,
11′
,
11′
则
 13′
13′

 16′
16′
20. (1)设
 ∴
∴ ∴
∴
由
又∵ ∴
∴
∴ 6′
6′
于是
由 得
得 或
或 ; 由
; 由 得
得 或
或
故函数 的单调递增区间为
的单调递增区间为 和
和 ,
,
单调减区间为 和
和 10′
10′
(2)证明:据题意 且x1<x2<x3,
且x1<x2<x3,
由(1)知f (x1)>f (x2)>f (x3),

 14′
14′


即ㄓ 是钝角三角形.
18′
是钝角三角形.
18′
第Ⅱ部分 加试内容
一.必答题:
1.(1)记事件A为“任取两张卡片,将卡片上的函数相加得到的函数是奇函数”,由题意知 4′
4′
(2)ξ可取1,2,3,4.
 ,
,
 ; 8′
; 8′
故ξ的分布列为
ξ
1
2
3
4
P





答:ξ的数学期望为 10′
10′
2.(1)由 得
得 ,
,
求得 3′
3′
(2)猜想 5′
5′
证明:①当n=1时,猜想成立。 6′
②设当n=k时 时,猜想成立,即
时,猜想成立,即 , 7′
, 7′
则当n=k+1时,有 ,
,
所以当n=k+1时猜想也成立 9′
③综合①②,猜想对任何 都成立。
10′
都成立。
10′
二、选答题:
 3.(1)∵DE2=EF?EC,
3.(1)∵DE2=EF?EC,
∴DE : CE=EF: ED.
∵ÐDEF是公共角,
∴ΔDEF∽ΔCED. ∴ÐEDF=ÐC.
∵CD∥AP, ∴ÐC=Ð P.
∴ÐP=ÐEDF.----5′
(2)∵ÐP=ÐEDF, ÐDEF=ÐPEA,
∴ΔDEF∽ΔPEA. ∴DE : PE=EF : EA.即EF?EP=DE?EA.
∵弦AD、BC相交于点E,∴DE?EA=CE?EB.∴CE?EB=EF?EP. 10′
4.(矩阵与变换)
解:.
 ,
5′
,
5′
椭圆 在
在 的作用下的新曲线的方程为
的作用下的新曲线的方程为 10′
10′
5.(1)直线的参数方程为 ,即
,即 . 5′
. 5′
(2)把直线 代入
代入 ,
,
得 ,
, ,
,
则点 到
到 两点的距离之积为
两点的距离之积为 .
10′
.
10′
6.
 7′
7′
当且仅当 且
且
F有最小值 10′
10′
