2007-2008学年度栖霞市第一学期期末质量检测
八年级数学试题
一、选择题(每小题4分,共48分,每小题有且只有一个正确答案)
1.下列说法正确的是
A.为了了解我市今年夏季冷饮市场冰淇淋的质量可采用普查的调查方式进行
B.为了了解一本300页的书稿的错别字的个数,应采用普查的调查方式进行
C.销售某种品牌的鞋,销售商最感兴趣的是所销售的鞋的尺码的平均数
D.为了了解我市九年级学生中考数学成绩,从所有考生的试卷中抽取1000份试卷进行统计分析,在这个问题中,样本是被抽取的1000名学生
2.若两个图形成位似关系,则下列说法不正确的是
A.每对对应点所在的直线都相交于同一点
B.两个图形上的对应线段必定平行
C.两个图形上的对应线段之比等于位似比
D.两个图形的面积比等于位似比的平方
3.下列计算正确的是
A.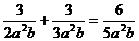 B.
B.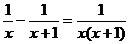
C.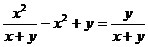 D.
D.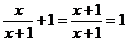
4.在二次根式 ,
,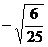 ,
,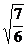 ,
,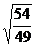 和
和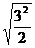 中,与
中,与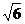 是同类根式的有
是同类根式的有
A.2个 B.3个 C.4个 D.5个
5.某校现有学生1800人,为了增强学生的法律意识,学校组织全体学生进行了一次普法测试。现抽取部分测试成绩(得分取整数)作为样本,进行整理后分成五组,并绘制成频数分布直方图。根据图中提供的信息,下列判断不正确的是
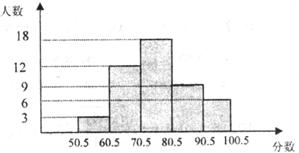
A.样本容量是48
B.估计本次测试全校在90分以上的学生约有225人
C.样本的中位数落在70.5~80.5这一分数段内
D.样本中50.5~70.5这一分数段的频率是0.25
6.某厂去年产值是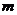 万元,今年产值是
万元,今年产值是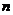 万元(
万元(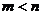 ),则今年的产值比去年的产值增加的百分比是
),则今年的产值比去年的产值增加的百分比是
A.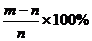 B.
B.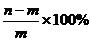
C.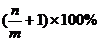 D.
D.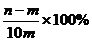
7.下列各组图形中相似的是( )

A.①②③ B.②③④ C.①③④ D.①②④
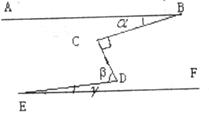
8.如图,AB∥EF,∠C=90°,则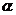 、
、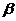 、
、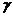 的关系为
的关系为
A.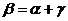 B.
B.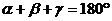
C.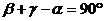 D.
D.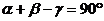
9.若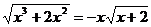 ,则
,则 的取值范围是
的取值范围是
A.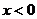 B.
B.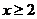 C.
C.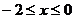 D.
D.
10.若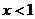 且
且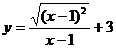 ,则
,则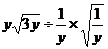 值是
值是
A. B.
B.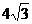 C.
C.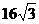 D.
D.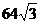
11.一个矩形的长为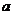 ,宽为
,宽为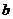 (
(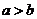 ),如果把这个矩形截去一个正方形后所余下的矩形与原矩形相似,那么
),如果把这个矩形截去一个正方形后所余下的矩形与原矩形相似,那么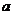 、
、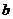 应满足的关系式是
应满足的关系式是
A. B.
B.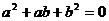
C.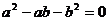 D.
D.
12.如图,已知BE是∠ABD的角平分线,CF是∠ACD的角平分线,BE、CF交于G,若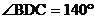 ,∠BGC=110°,则∠A的大小是
,∠BGC=110°,则∠A的大小是
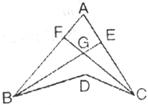
A.70° B.75° C.80° D.85°
二、填空题(每小题4分,共24分)
13.举出反例说明“如果AC=BC,那么点C是线段AB的中点”是个假命题:
14.化简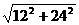 的结果是
的结果是
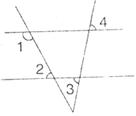
15.如图所示,∠1+∠2=180°,若∠3=50°,则∠4=
16.已知方程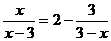 有增根,则这个增根一定是
有增根,则这个增根一定是
17.小明和小兵两人参加学校组织的理化实验操作测试,近期的5次测试成绩如下图所示,则小明5次成绩的方差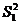 与小兵5次成绩的方差
与小兵5次成绩的方差 之间的大小关系为
之间的大小关系为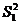
 (填“>”、“<”、“=”)
(填“>”、“<”、“=”)

18.两个相似多边形面积之比为5┱1,周长之比为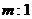 ,则
,则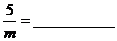
三、解答题(本大题8个小题,满分78分。要写出必要的文字说明、证明过程或演算步骤)
19.(本小题满分6分)当 分别取3,
分别取3,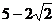 ,
,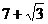 时,分别求代数式
时,分别求代数式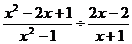 的值。
的值。
20.(本小题满分12分)计算与化简:
(1)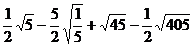
(2)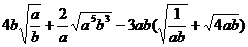
21.(本小题满分10分)为了进一步了解八年级学生的身体素质情况,体育老师对八年级(1)班50位学生进行一分钟跳绳次数测试,以测试数据为样本,绘制出部分频数分布表和部分频数分布直方图。如下所示:

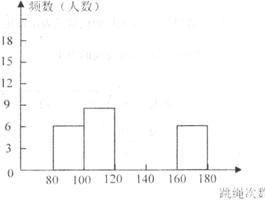
请结合图表完成下列问题:
(1)表中的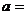 ;
;
(2)请把频数分布直方图补充完整;
(3)这个样本数据的中位数落在第 组;
(4)若八年级学生一分钟跳绳次数( )达标要求是:
)达标要求是: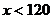 不合格;
不合格;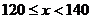 为合格;
为合格;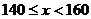 为良;
为良; 为优。根据以上信息,请你给学校或八年级同学提一条合理化建议:
为优。根据以上信息,请你给学校或八年级同学提一条合理化建议:
22.(本小题满分12分)已知直线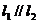 ,直线
,直线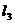 与直线
与直线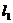 、
、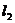 分别交于C、D两点。
分别交于C、D两点。
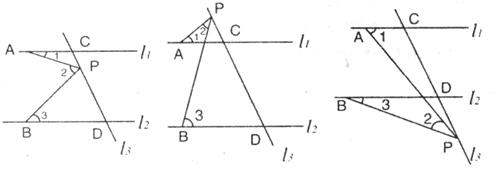
(1)如图a,有一动点P在线段CD之间运动(不与C、D两点重合),写出∠1、∠2、∠3之间的等量关系,并说明理由。
(2)如图b,当动点P在线段CD之外 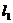 上方运动(不与C、D两点重合),写出∠1、∠2、∠3之间的等量关系。
上方运动(不与C、D两点重合),写出∠1、∠2、∠3之间的等量关系。
(2)如图c,当动点P在线段CD之外  下方运动(不与C、D两点重合),写出∠1、∠2、∠3之间的等量关系,并说明理由。
下方运动(不与C、D两点重合),写出∠1、∠2、∠3之间的等量关系,并说明理由。
23.(本小题满分12分)某公司需在一个月(31天)内完成新建办公楼装修工程。如果由甲、乙两队合做,12天可以完成;如果由甲、乙两队单独做,甲队单独完成所用的时间是乙队单独完成所用时间的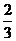 。
。
(1)求甲、乙两队单独完成此工程所需的时间。
(2)若请甲队施工,公司每日需付费用2000元;若请乙队施工,公司每日需付费用1400元。在规定时间内,有下列三种方案;
方案一:请甲队单独施工完成此工程;
方案二:请乙队单独施工完成此工程;
方案三:甲、乙两队合做完成此工程。
以上三种方案哪一种费用最少?
24.(本小题满分12,分)如图,在矩形ABCD中,E是BC上一点,且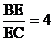 ,AE⊥DE。
,AE⊥DE。
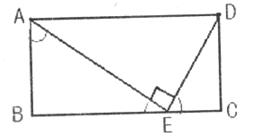
(1)找出图中所有的相似三角形,并说明其中的一组的理由;
(2)求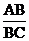 的值。
的值。
25.(本小题满分14分)问题一:通过验证可知,下列各式都是成立的。
 ,
,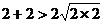 ;
;
 ,
,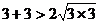 ;
;
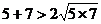 ,
,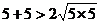 ;
;
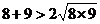 ,
,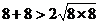 。
。
根据上面各组式子所反映的规律,回答问题:
(1)已知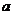 、
、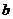 为正数,请写出
为正数,请写出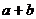 与
与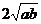 的大小关系;并指出
的大小关系;并指出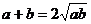 时,
时,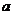 、
、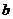 就满足的条件。
就满足的条件。
(2)请用你所学的知识,证明你的上述结论.
问题二:已知矩形的面积为64cm2,设它的长为 cm,周长为
cm,周长为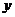 cm。
cm。
(1)填写下表并认真观察,然后说明矩形的长与宽有什么关系时,其周长最小?
(2)请用含 (cm)的代数式表示该矩形的周长
(cm)的代数式表示该矩形的周长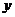 (cm),并用“问题一”中的知识解释你所发现的事实。
(cm),并用“问题一”中的知识解释你所发现的事实。
矩形长/cm
…
32
16
10
8
6.4
4
…
矩形宽/cm
…
…
其周长/cm
…
…