2008年清华中学初三一模试题
数 学 试 卷
注意事项:
1. 本试卷共4页27题,答题卡两张4面,考试时间120分钟,总分150分。
2. 请在答题卡的指定位置作上填写(涂)答案,否则无效。注意字迹清楚,保持整洁。
3. 请用
一、选择题(每小题3分,共6分)
1.下列计算正确的是( )
A.a2?a3=a6 B.(-a)3÷(-a)=a
2.下列图形中,是轴对称而不是中心对称图形的是 ( )
A.平行四边形 B.菱形 C.等腰梯形 D.直角梯形
3.电影院呈阶梯或下坡形状的主要原因是( ).
A.为了美观 B.盲区不变 C.增大盲区 D.减小盲区
4.六个学生进行投篮比赛,投进的个数分别是2,3,3,5,10,13这六个数的中位数为( )
A.3 B.4 C.5 D.6
5.已知两圆相交,其圆心距为6,大圆半径为8,则小圆半径r的取值范围是
A. r>2 B.2<r<14 C. r<8 D.2<r<8
6.从鱼塘年初放养的240尾鱼中,随机捞上9尾,称得质量分别是:1.5,1.6,1.4,1.6,1.3,1.4,1.2,1.7,1.8(单位:千克)。依次估计这240尾鱼总质量大约的千克数是
A.300 B.36 C.360 D.30
7.如图所示几何体的左视图是( )
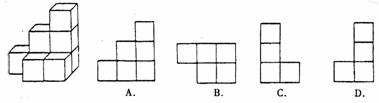
8.、如图,已知点A的坐标为(1,0),点B在直线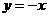 上运动,当线段AB最短时,点B的坐标为( )
上运动,当线段AB最短时,点B的坐标为( )
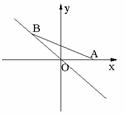
A.(0,0). B.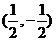 . C.
. C. 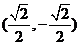 D.
D. 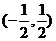 .
.
9.若使分式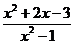 的值为0,则
的值为0,则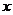 的取值为 ( )
的取值为 ( )
A.1或-1 B.-3或1 C.-3 D.-3或-1
10.如图,∠1=∠2,则下列结论一定成立的是( )
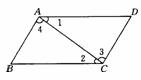
A.AB∥CD B.AD∥BC C.∠B=∠D D.∠3=∠4
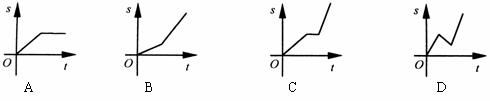
11.小明骑自行车上学,开始以正常速度匀速行驶,但行至中途自行车出了故障,只好停下来修车。车修好后,因怕耽误上课,他比修车前加快了骑车速度匀速行驶。下面是行驶路程s(米)关于时间t(分)的函数图像,那么符合这个同学行驶情况的图像大致是( )
12.如图,D,E分别是ΔABC中AB,AC上的点,添加下列条件后不能判定ΔABC与ΔAED相似的是 ( )
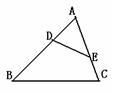
A.∠AED=∠ABC B.AD?AB=AC?AE
C.AD?AB=DE?AC D.∠ADE=∠C
二、填空题(每小题4分,共32分)
13、已知点P(-2,3),则点P关于x轴对称点的坐标是(_________)
14、据有关资料显示,长江三峡工程电站的总装机容量是18 200 000 000瓦,请你用科学记数法表示电站的总装机容量,应记为_________千瓦
15、化简-22 +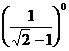 + 2sin30º=________.
+ 2sin30º=________.
16、函数y=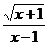 的自变量x的取值范围为________。
的自变量x的取值范围为________。
17、小明从前面的镜子里看到后面墙上挂钟的时间为2:30,则实际时间是___________。
18、若反比例函数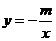 的图象经过点
的图象经过点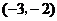 ,则
,则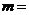 __________.
__________.
19、若圆的一条弦长为6 cm,其弦心距等于4 cm,则该圆的半径等于_____ cm.
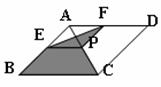
20. 如图,菱形ABCD的对角线的长分别为2和5,P是对角线AC上任一点(点P不与点A、C重合),且PE∥BC交AB于E,PF∥CD交AD于F,则阴影部分的面积是_______.
三、解答题(本题共7小题,共82分)
21、(每小题8分,共16分)
⑴先化简,再求值: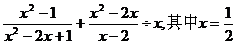
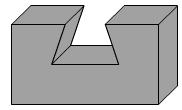
⑵画出下面实物的三视图:
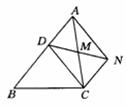
22、(8分)已知:如图,D是△ABC的边AB上一点,M是AC边的中点,过A作AN∥CD交DM延长线于N,
求证:AD=CN.
23. (10分)我国东南沿海某地的风力资源丰富,一年内日平均风速不小于3米/秒的时间共约160天,其中日平均风速不小于6米/秒的时间约占60天。
为了充分利用“风能”这种“绿色能源”,该地拟建一个小型风力发电场,决定选用A、B两种型号的风力发电机。根据产品说明,这两种风力发电机在各种风速下的日发电量(即一天的发电量)如下表:
日平均风速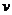 (米/秒)
(米/秒)
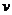 <3
<3
3≤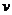 <6
<6
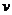 ≥6
≥6
日发电量(千瓦?时)
A型发电机
0
≥36
≥150
B型发电机
0
≥24
≥90
根据上面的数据回答:
(1)若这个发电场购 台A型风力发电机,则预计这些A型风力发电机一年的发电总量至少为_____________千瓦?时;
台A型风力发电机,则预计这些A型风力发电机一年的发电总量至少为_____________千瓦?时;
(2)已知A型风力发电机每台0.3万元,B型风力发电机每台0.2万元,该发电机拟购置风力发电机共10台,希望购机的费用不超过2.6万元,而建成的风力发电场每年的发电总量不少于102000千瓦?时,请你提供符合条件的购机方案。
24.(10分)如图,客轮沿折线A-B-C从A出发经B再到C匀速航行,货轮从AC的中点D出发沿某一方向匀速直线航行,将一批物品送达客轮。两船同时起航,并同时到达折线A-B-C的某点E处,已知AB=BC=200海里,∠ABC=90°,客轮速度是货轮速度的2倍。
(1)选择:两船相遇之处E点( )。
A、在线段AB上 B、在线段BC上C、可以在线段AB上,也可以在线段BC上
(2)求货轮从出发到两船相遇共航行了多少海里?(结果保留根号)。
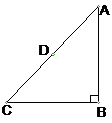
25. (12分)如图,以Rt△ABC的直角边AB为直径的半圆O,与斜边AC交于D,E是BC边上的中点,连结DE.
(1) DE与半圆O相切吗?若相切,请给出证明;若不相切,请说明理由;
(2) 若AD、AB的长是方程x2-10x+24=0的两个根,求直角边BC的长。
26.
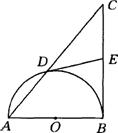
(14分)已知:如图,等腰梯形ABCD的边BC在x轴上,点A在y轴的正方向上,A( 0, 6 ),D ( 4,6),且AB=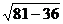 .
.
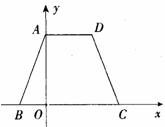
⑴求点B的坐标;
⑵求经过A、B、D三点的抛物线的解析式;
⑶在⑵中所求的抛物线上是否存在一点P,使得S△PBC = S梯形ABCD?若存在,请求出该点坐标,若不存在,请说明理由
27.(14分)如图,已知在矩形ABCD中,AD=8cm,CD=4cm,点E从点D出发,沿线段DA以每秒1cm的速度向点A方向移动,同时点F从点C出发,沿射线CD方向以每秒2cm的速度移动,当B、E、F三点共线时,两点同时停止运动.设点E移动的时间t(秒),
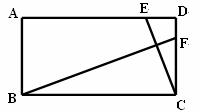
(1)求证:△BCF∽△CDE;
(2)求t的取值范围;
(3)连结BE,当t为何值时,∠BEC=∠BFC?