1、今年3月5日，温家宝总理在《政府工作报告》中，其中提到全国粮食连续四年增产，2007年产量达到50150万吨。这个产量数据保留两个有效数字用科学记数法表示为    （    ）

A．50×10⁷吨     B．5.0×10⁸吨    C．5.01×10⁸吨    D．5.02×10⁸吨

2、下列运算正确的是       （　　）

A. a²＋a³=a⁵                                B. （－2x）³=－2x³ 

C. （a－b）（－a＋b）=－a²－2ab－b²         D.  

3、用配方法解一元二次方程x²－4x－1=0，配方后得到的方程是   （     ）

    A．（x－2）²=1         B．（x－2）²=4          C．（x－2）²=5      D．（x－2）²=3

4、一物体及其正视图如下图所示，则它的左视图与俯视图分别是右侧图形中的  （     ）

A．①②                     B．③② 

C．①④                     D．③④

5、已知⊙O的半径为10 cm，一条弦AB=16 cm，则圆心O到弦AB的距离为   （     ）

A．10 cm                   B．8 cm                             C．6 cm                      D．5 cm

6、在同一坐标系内函数y=x+k与y=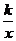的大致图像如图，其中正确的一个是  （     ）

7、“某市为处理污水，需要铺设一条长为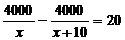4000米的管道，为了尽量减少施工对交通所造成的影响，实际施工时×××××。设原计划每天铺设管道x米，则可得方程。”根据此情境，题中用“×××××”表示得缺失的条件，应补为   （     ）

A．每天比原计划多铺设10米，结果延期20天才完成任务

B．每天比原计划少铺设10米，结果延期20天才完成任务

C．每天比原计划多铺设10米，结果提前20天完成任务

D．每天比原计划少铺设10米，结果提前20天完成任务

8、下列结论正确的个数是        （     ）

（1）一个多边形的内角和是外角和的3倍，则这个多边形是六边形

（2）如果一个三角形的三边长分别为6、8、10，则最长边上的中线长为5

（3） 若△ABC∽△DEF，相似比为1∶4，则S_△ABC∶S_△DEF=1∶4 .

（4）若等腰三角形有一个角为80°，则底角为80°或50°

        A．1                          B．2                            C．3                     D．4

9、在函数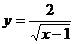中，自变量的取值范围是                ．

10、分解因式：=            ．

11、如图，在平行四边形ABCD中， ∠B=110^o，延长AD至F，延长CD至E，连接EF，∠E+∠F=              ．

12、已知圆锥母线长3， 侧面展开所得扇形的圆心角为120^o，则该圆锥的底面半径为    

          .

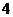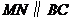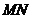13、如图，正方形的边长为，分别交AB，CD于点，在上任取两点，那么图中阴影部分的面积是           ．

14、计算：

15、解不等式组，并把解集在数轴上表示出来。       

16、请你先将下式化简，再选取一个你喜爱又使原式有意义的数代入求值：

17、如图，△ABC内接于⊙O，D是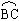的中点，AD交BC于E。

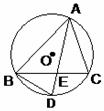
求证：。

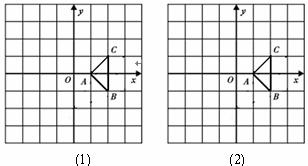
18、将图中的△分别作下列变换，在方格内画出相应的图形.                   

（1）关于轴对称；

    （2）以点O为位似中心，放大到2倍.

19、已知：如图，和都是等腰直角三角形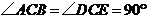，，为边上一点．

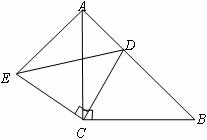
求证：（1）；

         （2）．

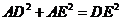20、为了让学生了解环保知识，增强环保意识，红星中学举行了一次“环保知识竞赛”，共有900名学生参加了这次竞赛．为了解本次竞赛成绩情况，从中抽取了部分学生的成绩（得分取正整数，满分为100分）进行统计．请你根据下面尚未完成并有局部污损的频数分布表和频数分布直方图，解答下列问题：

（1）填充频数分布表中的空格；

（2）补全频数分布直方图；

（3）全体参赛学生的成绩中，中位数落在哪个分组内？（不要求说明理由）

答：　　　　　　            　　　　　　。

（4）若成绩在90分以上（不含90分）为优秀，则该校成绩优秀的约为多少人？

答：　　　　　　　　             　　　　。  

21、已知抛物线的顶点是P，它与轴负半轴的交点是A，求直线PA的解析式。

五、解答题（本大题共3个小题；共36分．解答应写出文字说明、证明过程或演算步骤）

22、为缓解“停车难”问题，某单位拟建造地下停车库，建筑设计师提供了该地下停车库的设计示意图。按规定，地下停车库坡道口上方要张贴限高标志，以便告知停车人车辆能否安全驶入。其中AB=9米，BC=0.5米，CE⊥AD，为标明限高，请你根据该图计算CE。（精确到0.1米，已知sin18°≈0.3090，cos18°≈0.9511，tan18°≈0.3249）

23、某公司现有甲、乙两种品牌的计算器，甲品牌计算器有三种不同的型号，乙品牌计算器有两种不同的型号，新华中学要从甲、乙两种品牌的计算器中各选购一种型号的计算器．

（1）写出所有的选购方案（利用树状图或列表方法表示）；

（2）如果（1）中各种选购方案被选中的可能性相同，那么型号计算器被选中的概率是多少？

（3）现知新华中学购买甲、乙两种品牌两种型号的计算器共40个（价格如图所示），恰好用了1000元人民币，其中甲品牌计算器为型号计算器，求购买的型号计算器有多少个？

24、如图，有一块塑料矩形模板ABCD，长为10，宽为4，现有足够大的直角三角板PHF的直角顶点P落在AD边上（不与A、D重合），在AD上适当移动三角板顶点P：

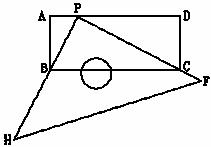
①能否使三角板两直角边分别通过点B与点C ？若能，请你求出这时AP 的长；若不能，请说明理由．

②再次移动三角板位置，使三角板顶点P在AD上移动，直角边PH始终通过点B，另一直角边PF与DC延长线交于点Q，与BC交于点E，能否使CE＝2？若能，请你求出这时AP的长；若不能，请你说明理由．