2007-2008学年度东营市第一学期期末质量调研
八年级数学试题
(考试时间:120分钟 分值:150分)
一.选择题(本题共12小题,每小题4分,满分48分.下面各题给出的四个选项中,只有一项是正确的,请将正确选项的代号填在题后的表格内).
1.一元二次方程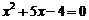 根的情况是( ).
根的情况是( ).
A. 两个不相等的实数根 B.两个相等的实数根
C. 没有实数根 D. 不能确定
2.如果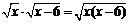 ,那么( )
,那么( )
A.x≥
3.若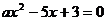 是一元二次方程,则不等式
是一元二次方程,则不等式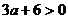 的解集是( )
的解集是( )
A. 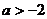 B.
B. 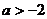 且
且 C.
C.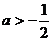 D.
D.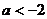
4.下列各式中,是最简二次根式的是( )
A.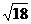 B.
B.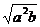 C.
C. 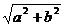 D.
D.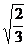
5.气象台预报“明天本市降雨的概率是80%”,对预测的正确理解是( )
A.本市明天有80%的地区降雨; B.本市明天将有80%的时间降雨;
C.明天出行不带雨具很可能会淋雨; D.明天出行不带雨具肯定会淋雨.
6.在⊙O中,弦AB垂直并且平分一条半径,则劣狐AB的度数等于( )
A.30° B.120° C.150° D.60°
7.小明把如图所示的扑克牌放在一张桌子上,请一位同学避开他任意将其中一张牌倒过来,然后小明很快辨认出被倒过来的那张扑克牌是( )

颠 倒 前 颠 倒 后
A. 方块5 B. 梅花
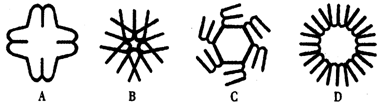
8.如图所示,下列四个图形都可以分别看成由一个“基本图案”经过旋转形成,则它们中旋转角相同的图形为( ).
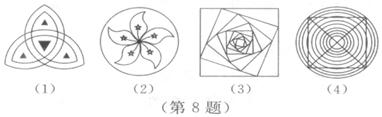
A.(1)(2) B.(1)(4) C.(2)(3) D.(3)(4)
9.下列图案都是由字母“m”经过变形,组合而成的,其中不是中心对称图形的是( ).
10.如图,在纸上剪下一个圆形和一个扇形的纸片,使之恰好能围成一个圆锥模型.若圆的半径为r,扇形的半径为R,扇形的圆心角等于90°,则r与R之间的关系是( )
A.R=2r; B.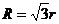 ; C.R=3r; D.R=4r.
; C.R=3r; D.R=4r.
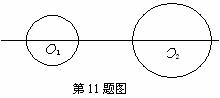
11.如图,已知⊙O1的半径为1,⊙O2的半径为2,圆心距O1O2=4。现把⊙O1沿直线O1O2平移,使⊙O1与⊙O2外切,则⊙O1平移的距离为( )
A. 1 B. 7 C. 1或7 D. 3或5
12.下列成语所描述的事件是必然发生的是( ).
A. 水中捞月 B. 拔苗助长 C. 守株待免 D. 瓮中捉鳖
二.填空题 (本大题共8小题,共32分.只要求填写最后结果,每小题填对得4分)
14.两圆有多种位置关系,图中不存在的位置关系是________.

15.等式│x-y│=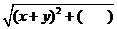 中的括号内应填入________.
中的括号内应填入________.
16.若用半径为r的圆形桌布将边长为60 cm的正方形餐桌盖住,则r的最小值为 .
17.若一个三角形的三边长均满足方程 ,则此三角形的周长为
,则此三角形的周长为
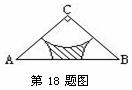
18.如图,在Rt△ABC中,∠C=90°,CA=CB=2。分别以A、B、C为圆心,以 AC为半径画弧,三条弧与边AB所围成的阴影部分的面积是______.
AC为半径画弧,三条弧与边AB所围成的阴影部分的面积是______.
19.从一定高度落下的图钉,落地后可能图钉针尖着地。也可能图钉针尖不着地,小丽同学在相同条件下做了这个实验。并将数据记录如下:
实验次数n
200
400
600
800
1000
针尖着地频数m
84
176
280
362
451
针尖着地频率
0.420
请将上表填完,钉尖着地的频率稳定到常数 (精确到0.01),所以估计此次实验钉尖着地的概率为 .
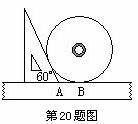
20.如图,小明同学测量一个光盘的直径,他只有一把直尺和一块三角板,他将直尺、光盘和三角板如图放置于桌面上,并量出AB=3.5cm,则此光盘的直径是_____ cm.
三.解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或推演步骤)
21.(本题10分)
如图,某学校计划在校园内修建一个正方形的花坛,在花坛中央还要修建一个正方形的小喷水池。搞设计需要考虑有关的周长,如果小喷水池的面积是8平方米,花坛的绿化面积为10平方米,问花坛的外围与小喷水池的周长一共是多少米?

22.(本题10分) 如图所示,正方形ABCD的BC边上有一点E,∠DAE的平分线交CD于F,试用旋转的思想方法说明AE=DF+BE.
23.(本题12分)
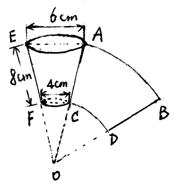
如图是一纸杯,它的母线AC和EF延长后形成的立方体图形是圆锥,该圆锥的侧面展开图是扇形OAB,经测量,纸杯上开口圆的直径是6cm,下底直径为4cm,母线长EF=8cm.
24.(本题12分) 节假日,小明和哥哥在水族馆看完海洋动物后,参加了出口处的抽奖活动.游戏的规则如下:每张门票只可摸球一次,每次从装有大小形状相同的2个白球和1个红球的盒子中,随机摸出一个球,若摸出的是红球,则获得一份奖品.
(1) 求每次摸球中奖的概率?
(2) 小明想:我有二张票,中奖的概率就翻一倍.你认为小明的思考正确吗?请用列表法或画树形图分析说明.
25.(本题12分)
在高度为2.8m的一面墙上,准备开凿一个矩形窗户。现用9.5m长的铝合金条制成如图所示的窗框。问:窗户的宽和高各是多少时,其透光面积为3m2(铝合金条的宽度忽略不计)。

26.(本题14分)
问题背景:某课外学习小组在一次学习研讨中,得到了如下两个命题:
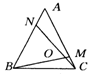
①如图1,在正三角形ABC中,M,N分别是AC,AB上的点,BM与CN相交于点O,若∠BON=60°,则BM=CN;
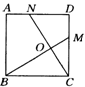
②如图2,在正方形ABCD中,M,N分别是CD,AD上的点,BM与CN相交于点O,若∠BON=90°,则BM=CN.
然后运用类比的思想提出了如下命题:
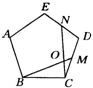
③如图3,在正五边形ABCDE中,M,N分别是CD,DE上的点,BM与CN相交于点O,若∠BON=108°,则BM=CN.任务要求:
(1)请你从①,②,③三个命题中选择一个进行证明;
(2)请你继续完成下面的探索:
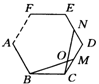
①如图4,在正n(n≥3)边形ABCDEF…中,M,N分别是CD,DE上的点,BM与CN相交于点O,试问当∠BON等于多少度时,结论BM=CN成立.(不要求证明)
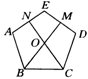
②如图5,在正五边形ABCDE中,M,N分别是DE,AE上的点,BM与CN相交于点O,若∠BON=108°时,试问结论BM=CN是否还成立.若成立,请给予证明;若不成立,请说明理由.