2008年贵阳市中考模拟试卷二
数学
一、选择题(以下每小题都有A、B、C、D四个选项,其中只有一个选项正确,请把正确选项的字母选入该题的括号内,每小题4分,共20分)
1.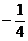 的绝对值是( )
的绝对值是( )
A.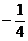 B.
B. C.
C. D.
D.
2.下列三条线段不能构成直角三角形的是( )
A.5cm,13cm,12cm B.2cm,3cm,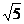 cm
cm
C.4cm,7cm,5cm D.1cm,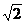 cm,
cm, cm
cm
3.某青年排球队12名队员的年龄情况如下:
年龄(单位:岁)
18
19
20
21
22
人 数
1
4
3
2
2
则这个队队员年龄的众数和中位数是( )
A.19,20 B.19,19 C.19,20.5 D.20,19
4.一元二次方程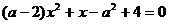 的一个根为0,则
的一个根为0,则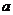 的值为( )
的值为( )
A.2 B.一2 C.一2或2 D.0
5.若点(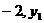 )、(1,
)、(1,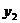 )、(3,
)、(3,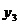 )都在反比例函数
)都在反比例函数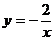 的图像上,则
的图像上,则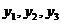 的大小关系是( )
的大小关系是( )
A.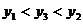 B.
B.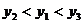 C.
C.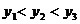 D.
D.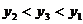
二、填空题(每小题3分,共30分)
6.长城总长约为6700010米,用科学记数法表示是(保留两个有效数字) .
7.分解因式: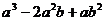 =
.
=
.
8.在一个口袋中装有1个黄球和3个红球,除颜色外完全相同,若一次摸出两个球都是红球的概率是 .
9.在一个晴朗的下午,小明和小红在操场上放风筝,小明发现自己的影子比小红的影子长0.5m.且知小明和小红的身高分别为1.7m和1.6 m。则小红影子的长是 m.
10.已知:如下图,AB∥DE,∠E=65°,则∠B+∠C的度数是

11.某学习小组调查了某县部分农民的家庭人口数,并绘制出下面扇形统计图(下图),这部分农民家庭的平均人口数为 人.

12.如下图,C是⊙O上一点,若圆周角∠ACB=40°,则圆心角∠AOB的度数是 .

13.如下图,一人乘雪橇沿坡比1: 的斜坡笔直滑下,滑下的距离s(米)与时间t(秒)间的关系为s=10t+2t2,若滑到坡底的时间为4秒,则此人下降的高度为 米.
的斜坡笔直滑下,滑下的距离s(米)与时间t(秒)间的关系为s=10t+2t2,若滑到坡底的时间为4秒,则此人下降的高度为 米.

14.一个正方体被一个平面所截,截面是一个边数为n的多边形,则n的最大值是 .
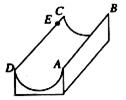
15.如下图是一个供滑板爱好者使用的U型槽,该U型槽可以看成是一个长方体去掉一个半圆柱而成,中间可供滑行部分的截面是半径为4m的半圆,其边缘AB=CD=20m,点E在CD上,CE=2m,一滑板爱好者从A点滑到E点,则他滑行的最短距离约为 m.(结果保留整数)
三、解答题
16.(本题6分)
已知不等式:(1)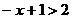 ;(2)
;(2)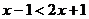 ;(3)
;(3)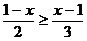 ;(4)
;(4) 请从这四个不等式中选择你喜欢的两个不等式,组成一个不等式组,并求出这个不等式组的解集.
请从这四个不等式中选择你喜欢的两个不等式,组成一个不等式组,并求出这个不等式组的解集.
17.(本题8分)
2007年某市国际车展期间,某公司对参观本次车展盛会的消费者进行了随机问卷调查,共发放1000份调查问卷,并全部收回.①根据调查问卷的结果,将消费者年收入的情况整理后,制成表格如下:
年收人(万元)
4.8
6.0
7.2
9.0
10.0
被调查的消费者人数(人)
200
500
200
70
30
②将消费者打算购买小车的情况整理后,作出频数分布直方图的一部分(下图).
注:每组包含最小值不包含最大值,且车价取整数.
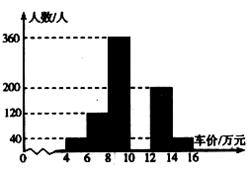
请你根据以上信息,回答下列问题:
(1)根据①中信息可得,被调查消费者的年收入的众数是 万元.(2分)
(2)请在图中补全这个频数分布直方图.(2分)
(3)打算购买价格10万元以下小车的消费者人数占被调查消费者人数的百分比是 .(3分)
18.(本题12分)
2007年5月17日某市荣获“国家卫生城市称号”.在“创卫”过程中,要在东西方向M、N两地之间修建一条道路.已知:如下图,C点周围180m范围内为文物保护区,在MN上点A处测得C在A的北偏东60°方向上,从A向东走500m到达B处,测得C在B的北偏西45°方向上.
(1)MN是否穿过文物保护区?为什么?(6分)
(2)若修路工程顺利进行,要使修路工程比原计划提前5天完成,需将原定的工作效率提高25%,则原计划完成这项工程需要多少天?(6分)

19.(本题12分)
小颖和小红两位同学在学习“概率”时,做抛骰子(质地均匀的正方体)实验,他们共做了60次实验.实验结果如下.
朝上的点数
1
2
3
4
5
6
出现的次数
7
9
6
8
20
10
(1)请计算“3点朝上”的频率和“5点朝上”的频率.(4分)
(2)小颖说:“根据实验,一次实验中出现5点朝上的概率最大.”;小红说:“如果投掷600次,那么出现6点朝上的次数正好是100次.”小颖和小红的说法正确吗?为什么?(4分)
(3)小颖和小红各投掷一枚骰子.用列表或画树状图的方法求出两枚骰子朝上的点数之和为3的倍数的概率.(4分)
20.(本题11分)
如下图,抛物线 与
与 轴交于点A、B,与
轴交于点A、B,与 轴交于点C,抛物线的顶点是D.
轴交于点C,抛物线的顶点是D.
(1)求点A、B、D的坐标;(3分)
(2)若点E在抛物线上,且E与C对称,求点E的坐标;(2分)
(3)若直线经过点C和B,求直线的表达式;(4分)
(4)根据图像,写出使二次函数的值大于零的 的取值范围.(2分)
的取值范围.(2分)

21.(本题10分)
如下图是一直径AB为4米,深BC为2米的圆柱形,在其里面挖去一个圆锥.
(1)求圆锥的母线长;(3分)
(2)若要把剩下的几何体刷上油漆,求这个几何体刷油漆部分的面积.(7分)

22.(本题12分)
某商场计划投入一笔资金采购一批紧俏商品,经过市场调查发现,如果月初出售,可获利15%,并可用本和利再投资其他商品,到月末又可获利10%;如果月末出售可获利30%,但要付出仓储费700元.假设商场投入的这笔资金是 (元),月初出售再把本和利再投资,月末所获总利为
(元),月初出售再把本和利再投资,月末所获总利为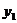 (元),月末出售所获利润为
(元),月末出售所获利润为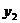 (元).
(元).
(1)请用 分别表示
分别表示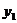 和
和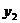 ;(4分)
;(4分)
(2)请问根据商场的资金状况,如何购销获利较多?(8分)
23.(本题10分)
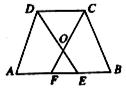
如下图,在梯形ABCD中,AD=BC,AB∥CD,E、F是边AB上的两点,且AE=BF,DE与CF相交于梯形ABCD内一点O.
(1)求证:OE=OF;(5分)
(2)当EF=CD时,请你连接DF、CE,判断四边形DCEF是什么样的四边形,并证明你的结论.(5分)
24.(本题10分)
某商场试销一种成本价60元/件的T恤,规定试销期间单价不能低于成本单价,又获利不高于40%,试销发现,销售量 (件)与销售单价
(件)与销售单价 (元/件)符合一次函数
(元/件)符合一次函数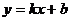 ,且
,且 =70时,
=70时, =50;
=50; =80时,
=80时, =40.
=40.
(1)求一次函数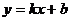 的表达式;(5分)
的表达式;(5分)
(2)若该商场获得利润W元,试写出利润W与 之间的关系式.销售单价定为多少时,商场可获得最大利润?最大利润是多少?(5分)
之间的关系式.销售单价定为多少时,商场可获得最大利润?最大利润是多少?(5分)
25.(本题9分)
△ABC内部共有若干个点,用这些点以及△ABC的顶点,把原三角形分割成一些三角形(如图).(1)填写下表:(6分)
△ABC内点的个数
1
2
3
4
…
n
分成的三角形的个数
3
5
…
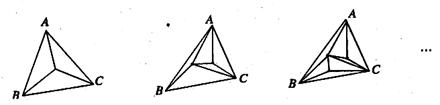
(2)原△ABC能否分成2008个三角形,若能,此时△ABC内部有多少个点;若不能,请说明理由.(3分)