2007-2008学年度淄博市沂源县第一学期期末考试
初二数学试题
(时间:120分钟 满分:150分)
一、选择题:本题共14小题,在每小题所给出的四个选项中,只有一个是正确的,请把正确的选项选出来.每小题4分,共56分,错选、不选或选出的答案超过一个,均记0分.
1、下列图形中,是轴对称图形的是( )
(A)锐角三角形 (B)钝角三角形 (C)直角三角形 (D)等边三角形
2、一个直角三角形的三边都是整数,其中一条长为5,则另外两条边长可以为( )
(A)4,6 (B)1,7 (C)12,13 (D)25,24
3、如图,△ABC与△A’
B’C’关于直线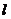 对称,则∠B的度数为( )
对称,则∠B的度数为( )

(A)30° (B)50° (C)90° (D)100°
4、如果一次函数 的图象经过第一象限,且与
的图象经过第一象限,且与 轴负半轴相交,那么( )
轴负半轴相交,那么( )
(A)k>0,b>0 (B)k>0,b<0 (C)k<0,b>0 (D)k<0,b<0
5、方程组 的解为( )
的解为( )
(A) (B)
(B) (C)
(C) (D)
(D)
6、估计 的大小应在( )范围内
的大小应在( )范围内
(A)9~10 (B)8.5~9 (C)8~8.5 (D)7~8
7、下列说法中,不正确的是( )
(A)每个数都有立方根 (B)0的立方根是0
(C)负数的立方根是负数 (D)1的立方根是1和―1
8、如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为10cm,正方形A的边长为6cm、B的边长为5cm、C的边长为5cm,则正方形D的边长为( )

(A) cm (B)4cm (C)
cm (B)4cm (C) cm (D)3cm
cm (D)3cm
9、甲、乙二人沿相同的路线由A到B匀速行进,A,B两地间的路程为20km.他们行进的路程s(km)与甲出发后的时间t(h)之间的函数图像如图所示.根据图像信息,下列说法正确的是( )
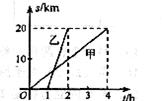
(A)甲的速度是4 km/h (B)乙的速度是10 km/h
(C)乙比甲晚出发1 h (D)甲比乙晚到B地3 h
10、小刚与小亮一起玩一种转盘游戏.如图是两个完全相同的能自由转动的转盘,每个转盘分成面积相等的三个区域,分别用“1”、“2”、“3”表示.固定指针,同时转动两个转盘,停止时,若两指针指的数字和为奇数,则小刚获胜;否则,小亮获胜.则在该游戏中小刚获胜的概率是( )

(A)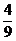 (B)
(B)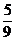 (C)
(C)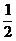 (D)
(D)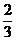
11、在平行于y轴的直线上,任意两点的坐标之间的关系是( )
(A)横坐标相等 (B)纵坐标相等
(C)横、纵坐标的绝对值都相等 (D)纵坐标的绝对值相等
12、把方程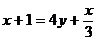 化成
化成 的形式,正确的是( )
的形式,正确的是( )
(A)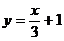 (B)
(B)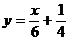 (C)
(C) (D)
(D)
13、在直角坐标系中,将坐标(0,0),(2,4),(2,0),(4,4)的点用线段依次连接起来,形成一个图案.经过下列变化得到的图案,与原图案相比,形状和大小都不变的是( )
(A)四个点的纵坐标不变,横坐标变成原来的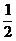
(B)四个点的横坐标和纵坐标分别乘一3
(C)四个点的纵坐标不变,横坐标分别加2
(D)四个点的横坐标不变,纵坐标乘2
14、2008年奥运会日益临近,某厂经授权生产的奥运纪念品深受人们欢迎,2007年1月份以来,该产品原有库存量为m(m>0)的情况下,日销量与产量持平,2007年3月底以来需求量增加,在生产能力不变的情况下,该产品一度脱销,下图能大致表示2007年1月份以来库存量y与时间t之间函数关系的是( )
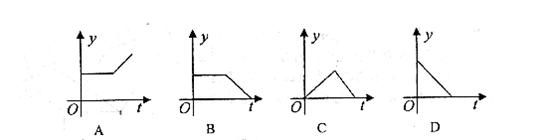
二、填空题:本题共6小题,每小题4分,共24分,只要求填写最后结果.
15、写一个有两条对称轴的轴对称图形 .
16、点(2,3)关于原点的对称点是 .
17、若a的立方根是2,则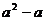 =
.
=
.
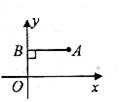
18、如图,在直角坐标平面内,线段AB垂直于y轴,垂足为B,且AB=2,如果将线段AB沿y轴翻折,点A落在点C处,那么点C的横坐标是 .
19、已知函数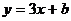 和
和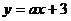 的图象交于点P(一1,0),则
的图象交于点P(一1,0),则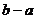 为
.
为
.
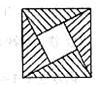
20、我国古代数学家赵爽的“勾股圆方图”是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形(如图所示).如果大正方形的面积是13,小正方形的面积是1,直角三角形的两直角边分别为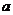 、b,那么
、b,那么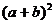 的值是
.
的值是
.
三、解答题:本大题共8小题,共70分.解答要写出必要的文字说明演算步骤.
21、解方程组(每小题5分,共10分)
(1)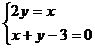
(2)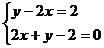
22、(本题满分8分)
已知第一个立方体纸盒的棱长是6厘米,第二个立方体纸盒的体积比第一个立方体纸盒的体积大127立方厘米,求第二个纸盒的棱长.
23、(本题满分8分)
如图,在四边形ABCD中,AB=20,BC=15,CD=7,AD=24,∠B=90°,求∠D的度数.
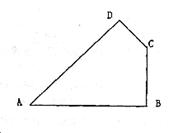
24、(本题满分8分)
等腰三角形中一个角是另一个的两倍,求各角的度数.
25、(本题满分9分)
购买作业本每个0.6元,若数量不少于13本,则按8折优惠.
(1)写出应付金额y元与购买数量 元之间的函数关系式:
元之间的函数关系式:
(2)求购买5本、20本的金额;
(3)若需12本作业本,怎样购买合算?
26、(本题满分9分)
从分别写有1、2、3的三张卡片中任意抽取一张,记下数字后放回,再任意抽取一张,记下数字,这两个数字之和为m,求:
(1) 两次数字相同的概率;(2)m为4的概率.
27、(本题满分9分)
“种粮补贴”惠农政策的出台,大大激发了农民的种粮积极性,某粮食生产专业户去年计划生产小麦和玉米共18吨,实际生产了20吨,其中小麦超产12%,玉米超产10%,该专业户去年计划生产小麦、玉米各多少吨?
28、(本题满分9分)
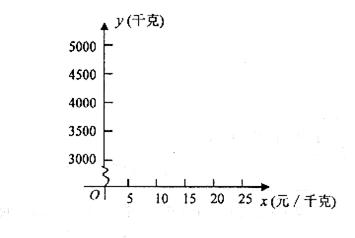
通过市场调查,一段时间内某地区某一种农副产品的需求数量y(千克)与市场价格 (元/千克)(0<
(元/千克)(0< <30)存在下列关系:
<30)存在下列关系:
 (元/千克)
(元/千克)
5
10
15
20
 (千克)
(千克)
4500
4000
3500
3000
假设该地区这种农副产品在这段时间内的生产数量z(千克)与市场价格 (元/千克)成正比例关系:z=400
(元/千克)成正比例关系:z=400 (0<
(0< <30).
<30).
现不计其它因素影响,如果需求数量y等于生产数量z,那么此时市场处于平衡状态.
(1)请通过描点画图探究y与 之间的函数关系,并求出函数关系式;
之间的函数关系,并求出函数关系式;
(2)根据以上市场调查,请你分析:当市场处于平衡状态时,该地区这种农副产品的市场价格与这段时间内农民的总销售收入各是多少?