2006-2007学年度济宁市微山县第二学期期末考试
七年级数学试题
一、选择题(本题共12小题,共36分,在每小题给出的四个选项中,只有一个是正确的,请把正确的选项选出来,把序号填在答案栏里。每小题选对得3分,选错、不选或选出的答案超过一个均记零分。)
1、在实数 ,3.1415926,
,3.1415926, ,
, ,
, ,4.15中,无理数的个数有( )
,4.15中,无理数的个数有( )
A.2个 B.3个 C.4个 D.5个
2、已知点P(m+3,m+1)在X轴上,那么点P的坐标为( )
A.(0, -2) B.(2, 0) C.(4, 0) D.(0, 4)
3、如果a>b,那么下列结论正确的是( )
A. B.4-a<4-b C.a-3>b-2 D.
B.4-a<4-b C.a-3>b-2 D.
4、小明有两根长度分别为3厘米,5厘米的木棒,要选择第三根木棒做成三角形,现有2厘米、4厘米、6厘米、8厘米、10厘米的木棒各一根.则可供小明选用木棒有( )
A.2根 B.3根 C.4根 D.5根
5、《九章算术》是我国东汉初年编订的一部数学经典著作,在它的“方程”一章里,一次方程组是由算筹布置而成的。《九章算术》中的算筹图是竖排的,为看图方便,我们把它改为横排,如图1-1、图l-2,图中各行从左到右列出的算筹数分别表示未知数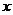 、
、 的系数与相应的常数项。把图1-1所示的算筹图用我们现在所熟悉的方程组形式表述出来,就是
的系数与相应的常数项。把图1-1所示的算筹图用我们现在所熟悉的方程组形式表述出来,就是 。类似地,图1-2所示的算筹图我们可以表述为( )
。类似地,图1-2所示的算筹图我们可以表述为( )

A. B、
B、
C、 D、
D、
6、下列说法中正确的是( )
A.64的立方根是±4 B. 是
是 的一个平方根
的一个平方根
C.平方根等于本身的数是0,1 D.立方根等于本身的数是0
7、下列说法中错误的个数是( )
(1)过一点有且只有一条直线与已知直线平行。
(2)过一点有且只有一条直线与已知直线垂直。
(3)在同一平面内,两条直线的位置关系只有相交、平行两种。
(4)不相交的两条直线叫做平行线。
(5)有公共顶点且有一条公共边的两个角互为邻补角。
A.5 B.
8、下列等式中,错误的是( )
A. B.
B.
C. D.
D.
9、如图2,△ABC中,∠ABC和∠ACB的平分线交于点O,∠BOC=120°,则∠A=( )

A.30° B.40° C.55° D.60°
10、四个电子宠物排座位,一开始,小鼠、小猴、小免、小猫分别坐在1、2、3、4号座位上(如图3所示),以后它们不停地变换位置,第一次上下两排交换,第二次是在第一次换位后,再左右两列交换位置,第三次上下两排交换,第四次再左右两列交换……这样一直下去,则第2005次交换位置后,小兔子坐在( )号位上。

A.1 B.
11、一次智力测验,有20道选择题。评分标准是:对l题给5分,错1题扣2分,不答题不给分也不扣分。小明有两道题未答,至少答对几道题,总分才不会低于60分。则小明至少答对的题数是( )
A.12题 B.13题 C.14题 D.15题
12、如图4,是测量一物体体积的过程:

步骤一:将180ml的水装进一个容量为300ml的杯子中;
步骤二:将三个相同的玻璃球放入水中,结果水没有满;
步骤三:同样的玻璃球再加一个放入杯中,结果水满溢出。
根据以上过程,推测一颗玻璃球的体积在下列哪个范围内(1ml=
A、
C、
二、填空题(共6小题,每小题3分,计18分)
13、 算术平方根是
。
算术平方根是
。
14、写出一个解为 的二元一次方程
。
的二元一次方程
。
15、如图5,在同一平面直角坐标系中,△ABC的顶点坐标分别为A(-8, 0),B(2, 0),C(-2, 5),则△ABC的面积是 。



16、生活中,将一个宽度相等的纸条按图6所示折叠一下,如果∠1=140°,那么∠2= 。
17、如图7,把直角梯形ABCD沿AD方向平移到梯形EFGH,HG=
18、小亮解方程组 的解为
的解为 ,由于不小心,滴上了两滴墨水,刚好遮住了两个数●和★,请你帮他找回这两个数●=
,★= 。
,由于不小心,滴上了两滴墨水,刚好遮住了两个数●和★,请你帮他找回这两个数●=
,★= 。
三、解答题:(本题共7个小题,共66分)
19、(本题6分)
20、(本题12分)
(1)解方程组:
(2)求不等式组 的解集。
的解集。
21、(本题10分)已知:方程组 的解为
的解为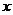 、
、 ,且
,且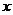 、
、 都是正数。
都是正数。
(1)求a的取值范围
(2)化简
22、(本题l0分)今年6月3号我国云南普洱境内发生里氏6.4级地震,给当地人民造成巨大的经济损失。某学校积极组织捐款支援灾区,初一(1)班有55名同学共捐款274元,捐款情况见下表,表中捐款2元和5元的人数不小心被墨水污染已经看不清楚,请你帮助确定表中的数据,并说明理由。

23、(本题9分)。
(1)如图①∠1+∠2与∠B+∠C有什么关系?为什么?
(2)把图①△ABC沿DE折叠,得到图②,填空:∠1+∠2 ∠B+∠C(填“>”“<”“=”),当∠A=40°时,∠B+∠C+∠1+∠2= 。
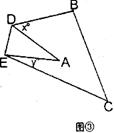
(3)如图③,是由图①的△ABC沿DE折叠得到的,猜想∠BDA+∠CEA与∠A的关系是怎样的?为什么?如果∠A=30°时,则x+y的度数是多少?


24、(本题9分)如图8,已知A、B是△ABC的两个顶点,P、Q是△PQK的两个顶点,且△PQR是△ABC经过某种变换后得到的图形。

(1)分别写出点A与点P,点B与点Q的坐标,并说明它们之间的关系?
(2)若点C的坐标为(x, y+1),点R的坐标为(x-2, y-3),且点C与点R也具有(1)中的关系,试求点C与点R的坐标,并画出△ABC与△PQR。
(3)把△PQR向上平移4个单位长度,画出平移后的新△P’Q’R’,并写出顶点坐标。
25、(本题10分)暑假期间,某学校准备组织学生参加夏令营活动,如果单独租用45座客车若干辆,刚好坐满;如果单独租用60座客车,可以少租一辆,且空余30个座位。
(1)求参加夏令营活动的学生人数。
(2)如果45座客车每辆租金为250元,60座客车每辆租金为300元,这次活动同时租用两种客车,其中60座比45座客车多l辆,所用租金比单独租用任何一种客车所需费用都低,按这种方案所需费用是多少?