2006-2007学年度潍坊市诸城第二学期期末考试
八年级数学试题
一、选择题（下列每小题给出的四个答案中，有且只有一个答案是正确的，请将正确答案的字母代号填入题后括号内，每小题3分，共30分）
1．已知分式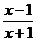
的值是零，那么
的值是（ ）
A．－1 B．0 C．1 D．±1
2．下列说法中，正确的是（ ）
A．每个命题都有逆命题 B．每个定理都有逆定理
C．真命题的逆命题是真命题 D．假命题的逆命题是假命题
3．已知点A（－1，0），B（1，1），C（0，－3），D（－1，2），E（0，1），F（6，0），其中在坐标轴上的点有（ ）
A．1个 B．2个 C．3个 D．4个
4．某车间6月上旬生产零件的次品数如下（单位：个）：0，2，0，2，3，0，2，3，1，2则在这10天中该车间生产零件的次品数的（ ）
A．众数是4 B．中位数是1.5 C．平均数是2 D．方差是l.25
5．在四边形ABCD中，AD∥BC，AB=DC，则四边形ABCD是（ ）
A．等腰梯形 B．平行四边形
C．直角梯形 D．等腰梯形或平行四边形
6．反比例函数
的图像在每个象限内，
随的增大而减小，则
的值可为（ ）
A．－l B．0 C．1 D．2
7．若点P（
，
）在第二、四象限内的两坐标轴的角平分线上，则与的关系是（ ）
A．
B．
C．
D．
8．下列判断中正确的是（ ）
A．四边相等的四边形是正方形
B．四角相等的四边形是正方形
C．对角线互相垂直的平行四边形是正方形
D．对角线互相垂直平分且相等的四边形是正方形
9．在下列图形中，沿着虚线将长方形剪成两部分，那么由这两部分既能拼成三角形，又能拼成平行四边形和梯形的可能是（ ）
10．在平面直角坐标系中，□ABCD的顶点A、B、D的坐标分别是
，
，
，则顶点C的坐标是（ ）
A（3，7） B．（5，3） C．（7，3） D．（8，2）
二、填空题（每小题2分，共20分）
11．计算：
。
12．皂泡表面厚度大约是
13．甲、乙两台机器分别罐装每瓶质量为
，
那么 （填“甲”或“乙”）罐装的矿泉水质量比较稳定。
14．在扇形统计图上，有一个数据是27％，在表示这个数据中，两条半径所夹的角约为 度。（精确到个位）
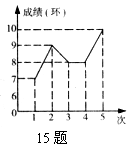
15．如图是小敏五次射击成绩的折线图，根据图示信息，则此五次成绩的平均数是 环。
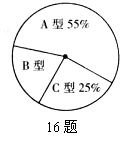
16．在暑期社会实践活动中，小明所在小组的同学与一家玩具厂联系，给该厂组装玩具，该厂同意他们组装240套玩具，这些玩具分为A、B、C三种型号，它们的数量比例以及每人每小时组装各种型号玩具的数量如图所示：
若每人组装同一种型号玩具的速度都相同，根据以上信息，完成下列填空：
从上述统计图可知，A型玩具有 套，B型玩具有 套，C型玩具有 套。
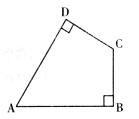
17．如上图，已知∠CDA=∠CBA=90°，且CD=CB，则点C一定在 的平分线上，点A在 的平分线上。
18．方程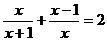
的解是
。
19．摩托车油箱中有汽油公升，摩托车已经跑过的路程为km，则与的函数关系式是 ，自变量的取值范围是
。
20．本题为选做题，若两题都做，按（A）题记分。
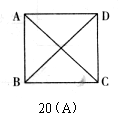
（A）如图，若四边形ABCD是矩形，要使四边形 ABCD为正方形，还需增加条件 。（只需填一个即可）
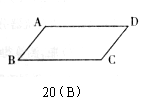
（B）如图，AD=BC，要使四边形ABCD是平行四边形，还需补充的一个条件是 。（只需填一个即可）
三、解答题（共65分）
21．（5分）
已知三个自然村，A、B、C的位置如图所示，现计划建一所学校，使其到三个村的距离相等请你设计出学校所在的位置。（不写画法，保留作图痕迹）。
22．（7分）
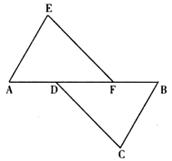
如图，A、D、F、B在同一直线上， AD=BF，AE=BC，且AE∥BC。
求证：（1）△AEF≌△BCD；（2）EF∥CD。
23．（7分）
为了调查八年级某班学生每天完成家庭作业所需的时间，在该班随机抽查了8名学生，他们每天完成作业所需时间（单位：分）分别为：
60，55，75，55，55，43，65，40．
（1）求这组数据的众数、中位数；
（2）求这8名学生每天完成家庭作业的平均时间；如果按照学校要求，学生每天完成家庭作业时间不能超过60分钟，问该班学生每天完成家庭作业的平均时间是否符合学校的要求？
24．（7分）
地表以下岩层的温度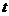
（℃）随着所处的深度
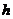（千米）的变化而变化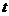，与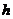之间在一定范围内近似地成一次函数关系。
（1）根据下表，求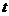（℃）与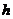（千米）之间的函数关系式；
（2）求当岩层温度达到
温度（℃）
…
90
160
300
…
深度（km）
…
2
4
8
…
25．（8分）
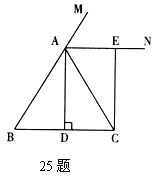
已知，如图，在△ABC中，AB=AC，AD⊥BC，垂足为点D，AN是△ABC外角∠CAM的平分线，CE⊥AN，垂足为点E。
（1）求证：四边形ADCE为矩形；
（2）当△ABC满足什么条件时，四边形ADCE是一个正方形？并给出证明。
26．（7分）
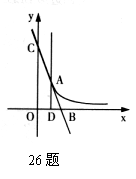
如图，直线
与双曲线
是只有一个交点A（1，2），且与轴、轴分别交于B、C两点，AD垂直平分OB，垂足为D，求直线、双曲线的解析式。
27．（7分）
甲、乙两工程队分别承担一条千米，另一半时间每天维修公路千米，乙队维修前千米；维修后千米（
）。
（1）求甲、乙两队完成任务各自需要的时间（用含，的代数式表示）；
（2）问甲、乙两队哪队先完成任务？
28．（8分）
已知：如图，在□ABCD中，E、F分别为边AB、CD的中点，BD是对角线，AG∥DB交CB的延长线于G。
（1）求证：△ADE≌△CBF；
（2）若四边形BEDF是菱形，则四边形AGBD是什么特殊四边形？并证明你的结论。
29．（9分）
为解决台湾民众水果销售困难问题，国家规定，对原产台湾地区的15种水果实施进口零关税措施，扩大了台湾水果在大陆的销售。某经销商销售了台湾水果凤梨，根据以往销售经验，每天的售价与销售量之间有如下关系：
每千克售价（元）
38
37
36
35
…
20
每天销量（千克）
50
52
54
56
…
86
设当单价从38元/千克下调了元时，销售量为千克；
（1）写出与间的函数关系式；
（2）如果凤梨的进价是20元/千克，某天的销售价定为30元/千克，问这天的销售利润是多少？
（3）如果运输要绕行，需耗时一周（七天），凤梨最长的保存期为一个月（30天），若每天售价不低于30元/千克，问一次进货最多只能是多少千克？