2007-2008学年度日照市五莲县上学期期末质量调查
九年级数学试题
(时间 l00分钟 总分120分)
一、选择题:(本题共12小题,第l~8小题,每小题3分,第9~12小题,每小题4分,共40分。在每小题给出的四个选项中,只有一项是正确的,请你把正确的选项选出来,把选项的代号填在下面表格中。)
1.下列计算正确的是
A.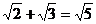 B.
B.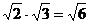
C.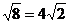 D.
D. 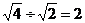
2.当m<0时,化简 的结果是
的结果是
A.一l B.
3.下列图形中,中心对称图形是

4.正方形ABCD中,点P是对角线AC上的任意一点(不包括端点),以P为圆心的圆与AB相切,则AD与⊙P的位置关系是
A.相切 B.相离 C.相交 D.不确定
5.下面有关概率的叙述,正确的是
A.因为购买彩票时有“中奖”与“不中奖”两种情形,所以购买彩票中奖的概率为
B.投掷一枚硬币,正面朝上的概率和正面朝下的概率不相同
C.随机事件发生的概率大于0且小于1
D.某种彩票的中奖概率是1%,买100张这样的彩票一定中奖
6.如图,不等长的两对角线AC、BD相交于D点,且将四边形ABCD分成甲、乙、丙、丁四个三角形。若OA:OC=OB:OD=1:2,则此四个三角形的关系是

A.甲丙相似,乙丁相似 B.甲丙相似,乙丁不相似
C.甲丙不相似,乙丁相似 D.甲丙不相似,乙丁不相似
7.如图,小明同学测量一个光盘的直径,他只有一把直尺和一块三角板,他将直尺、光盘和三角板如图放置于桌面上,并量出AB=
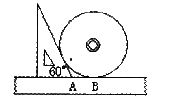
A. cm C.3
cm C.3 cm D.6
cm D.6 cm
cm
8.如图,将半径为2cm的圆形纸片折叠后,圆弧恰好经过圆心O,则折痕AB的长为

A.2cm B. cm C.2
cm C.2 cm D.2
cm D.2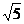 cm
cm
9.在同一坐标平面内,图象不可能由函数 的图象通过平移变换、轴对称变换得到的函数是
的图象通过平移变换、轴对称变换得到的函数是
A. B.
B.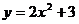
C. D.
D.
10.已知函数 的图象如图所示,那么关于
的图象如图所示,那么关于 的方程
的方程 的根的情况是
的根的情况是

A.无实数根 B.有两个相等实数根
C.有两个异号实数根 D.有两个同号不等实数根
11.将一块圆心角为120°,弧长为2 的扇形铁皮围成一个圆锥(接头忽略不计),则围成的圆锥的高为
的扇形铁皮围成一个圆锥(接头忽略不计),则围成的圆锥的高为
A. B.2
B.2 C.2
C.2 D.
D.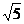
12.已知抛物线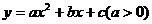 的对称轴为直线
的对称轴为直线 与
与 轴的一个交点为(
轴的一个交点为( ,0),且0<
,0),且0< <1,下列结论:①
<1,下列结论:①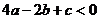 ;②
;② ;③
;③ >c。其中正确结论的个数是
>c。其中正确结论的个数是
A.0 B.1 C.2 D.3
二、填空题:(本题共有5小题,每小题4分,共20分)请把最终结果直接填在横线上。
13.已知 为整数,且满足
为整数,且满足 ,则
,则 =_____________.
=_____________.
14.若方程 的两根互为相反数,则m=__________.
的两根互为相反数,则m=__________.
15.如图,边长为3的正方形ABCD绕点C按顺时针方向旋转30°后得到正方形EFCG,EF交AD于点H,那么DH的长为______________.

16.如图,小正六边形沿着大正六边形的边缘顺时针滚动,小正六边形的边长是大正六边形边长的一半,当小正六边形由图①位置滚动到图②位置时,线段OA绕点O顺时针转过的角度为______________。
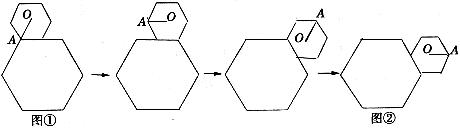
17.廊桥(如图一)是我国古老的文化遗产,如图二是某座抛物线型的廊桥示意图,跨度AB=40米,桥架的拱高OH为l0米,为保护廊桥的安全,在该抛物线上距水面AB高为8米的点E、F处要安装两盏警示灯,则这两盏灯的水平距离EF=__________米.

三、解答题:(本题共7小题,共60分。解答题都应写出文字说明、证明过程或推演步骤。)
18.(本题满分6分)
计算: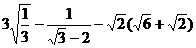
19.(本小题满分6分)
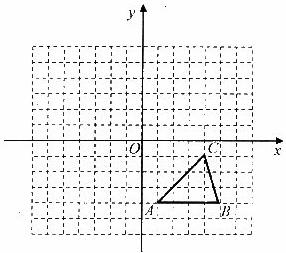
如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(4,一l).
(1)把△ABC向上平移5个单位后得到对应的△A1B1C1,画出△A1B1C1,并写出Cl的坐标;
(2)以原点O为对称中心,再画出与△A1B1C1关于原点O对称的△A2B2C2,并写出点C2的坐标.
20.(本题满分8分)
国家为了解决老百姓看病贵的问题,决定下调一些药品的价格.某种药品原售价为125元/盒,连续两次降价后售价为80元/盒.假设每次降价的百分率相同,求这种药品每次降价的百分率.
21.(本题满分8分)
在直角坐标平面内,二次函数图象的顶点为A(1,一4),且过点B(3,0)
(1)求该二次函数的解析式;
(2)将该二次函数图象向右平移几个单位,可使平移后所得图象经过坐标原点?并直接写出平移后所得图象与 轴的另一个交点的坐标.
轴的另一个交点的坐标.
22.(本题满分l0分)
如图,AB是半圆O的直径,AD是弦,E为弧 的中点,OE的延长线交切线AC(切点为A)于点C,连结BE,DE.
的中点,OE的延长线交切线AC(切点为A)于点C,连结BE,DE.

(1)求证:∠BED=∠C:
(2)若OA=5,AD=8,求AC的长.
23.(本题满分l0分)
张华和王平两位同学为得到一张观看足球比赛的入场券,各自设计了一种方案:
张华:如图,设计了一个可以自由转动的转盘,随意转动转盘,当指针指向阴影区域时,张华得到入场券;否则,王平得到入场券;
王平:将三个完全相同的小球分别标上数字1、2、3后,放入一个不透明的袋子中,从中随机取出一个小球,然后放回袋子;混合均匀后,再随机取出一个小球.若两次取出的小球上的数字之和为偶数,王平得到入场券;否则,张华得到入场券.
请你运用所学的概率知识,分析张华和王平的设计方案对双方是否公平.

24.(本题满分l2分)
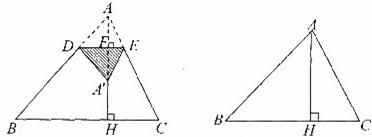
如图,在锐角△ABC中,BC=9,AH⊥BC于点H,且AB=6,点D为AB边上的任意一点,过点D作DE//BC,交AC于点E.设△ADE的高AF为 (0<
(0< <6),以DE为折线将△ADE翻折,所得的△A’DE与梯形DBCE重叠部分的面积记为
<6),以DE为折线将△ADE翻折,所得的△A’DE与梯形DBCE重叠部分的面积记为 (点A关于DE的对称点A’落在AH所在的直线上).
(点A关于DE的对称点A’落在AH所在的直线上).
(1)分别求出当0< ≤3与3<
≤3与3< <6时,y与
<6时,y与 的函数关系式;
的函数关系式;
(2)当 取何值时,y的值最大?最大值是多少?
取何值时,y的值最大?最大值是多少?