2007年张家口市中考模拟考试(二)数学试卷
本试卷分卷Ⅰ和卷Ⅱ两部分,卷Ⅰ为选择题,卷Ⅱ为非选择题。
本试卷满分为120分,考试时间为120分钟
卷Ⅰ(选择题,共20分)
一、选择题(本大题共10个小题;每小题2分,共20分。在每小题给出的四个选项中,只有一项是符合题目要求的)
1.计算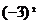 ,结果正确的是 ( )
,结果正确的是 ( )
A.-9 B.
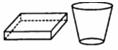
2.如下图。从左边看图中的物体,得到的图形是 ( )
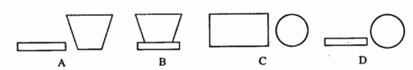
3.小马虎在下面的计算中只做对了一道题,他做对的题目是( )
A. B.
B.
C.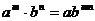 D.
D.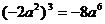
4.如图,在△ABC中,∠A=30°,∠B=50°,AC=AE,BC=BD,则∠DCE的度数为( )

A.20° B.25° C.30° D.40°
5.如图,水平放置的一个油管的截面为圆形,其直径为

A.
6.某商场出售甲、乙两种商品,售价都是1800元,其中甲商品能盈利20%,乙商品亏损20%,如果同时售出甲、乙商品各一件,那么( )
A.共盈利150元 B.共亏损150元 C.不赢也不亏 D.无法判断
7.下图是测量一物体体积的过程:
步骤一,将180ml的水装进一个容量为300名来的杯子中.
步骤二,将三个相同的玻璃球放入水中,结果水没有满.
步骤三,同样的玻璃球再加一个放入水中,结果水满溢出.

根据以上过程,请你判断一颗玻璃球的体积在下列哪一范围内(1ml=
A.
C.
8.如图,某运动员P从半圆跑道的A点出发沿 匀速前进到达终点B,若以时间
匀速前进到达终点B,若以时间 为自变量,扇形OAP的面积S为函数的图象大致是( )
为自变量,扇形OAP的面积S为函数的图象大致是( )


9.如图,反比例函数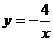 的图象与直线
的图象与直线 的交点为A、B,过点A作
的交点为A、B,过点A作 轴的平行线与过点B作
轴的平行线与过点B作 轴的平行线相交于点C,则△ABC的面积为( )
轴的平行线相交于点C,则△ABC的面积为( )
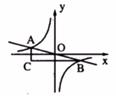
A.8 B.
10.某小区内有一块边长为a的正方形土地,园艺师设计了四种不同的图案,如下图所示,其中阴影部分用于种植花草,你认为种植花草部分面积最大的图案是( )
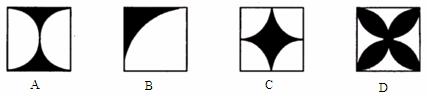
二、填空题(本大题共8个小题;每小题3分,共24分,把答案写在题中横线上)
11.分解因式: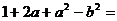 ______________.
______________.
12.用科学技术法表示0.0000106=______________.
13.某电视台举办歌手大奖赛,每场比赛都有编号为1~10号共10道综合素质题供选手随机抽取作答.在某场比赛中,前两位选手分别抽取了2号、7号题,那么第三位选手抽中8号题的概率是______________.
14.某款手机连续两次降价,售价由原来的1185元降到580元,设两次降价的平均百分率为 ,则可列方程为______________.
,则可列方程为______________.
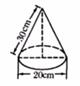
15.如图,是小顺制作的一个圆锥形纸帽的示意图,则围成这个纸帽的纸的面积为_________.
16.如图,△ABC是等腰直角三角形,BC是斜边,点P是△ABC内一定点,延长BP至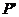 ,将△ABP绕点A旋转后,与△ACP′重合,如果
,将△ABP绕点A旋转后,与△ACP′重合,如果 ,那么
,那么 _________.
_________.

17.下图是小明用火柴搭的1条、2条、3条“金鱼”……,则搭 条“金鱼”需要火柴_______根
条“金鱼”需要火柴_______根

18.如图所示,某校宣传栏(图中的AB)后面

三、解答题(本题共8个小题;共76分)
19.(本小题满分8分)
已知 ,求
,求 的值.
的值.
20.(本小题满分8分)
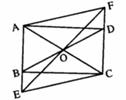
如图,矩形ABCD中,O是AC与BD的交点,过O点的直线EF与AB、CD的延长线分别交于点E、F.
(1)求证:△BOE≌△DOF;
(2)连接EC、AF,当EF与AC满足什么条件时,四边形AECF为菱形,并说明理由.
21.(本小题满分8分)
如图,图(1)是某中学初三(A)班全体学生对三种蔬菜的喜欢人数的频数分布直方图,解答下列问题:
(1)初三(A)班总人数为_______人;
(2)喜欢人数频率最高的蔬菜是_______,且频率为_______;
(3)请根据各统计图中的数据,补全图(1)、(2)中的统计图;
(4)根据上述统计的结果,请你为食堂的进货提出一条合理化的建议.

建议:
22.(本小题满分8分)
如图,花丛中有一路灯杆AB,在灯光下,小明在D点处的影长DE=

23.(本小题满分10分)
某空军加油飞机接到命令,立即给另一架正在飞行的运输机进行空中加油,在加油过程中,设运输飞机的油箱余油量为 吨,加油飞机的加油油箱余油量为
吨,加油飞机的加油油箱余油量为 吨,加油时间为
吨,加油时间为 分钟,
分钟, 、
、 与
与 之间的函数图象如图所示,结合图象回答下列问题:
之间的函数图象如图所示,结合图象回答下列问题:

(1)加油飞机的加油油箱中装载了多少吨油?将这些油全部加给运输飞机需要多少分钟?
(2)在加油过程中,运输飞机的余油量 (吨)与时间
(吨)与时间 (分钟)的函数关系式;
(分钟)的函数关系式;
(3)运输飞机加完油后,以原速继续飞行,需10小时到达目的地,油料是否够用?请说明理由.

证明:在矩形ABCD中,OE⊥BC,DC⊥BC,∴OE∥DC.
∵ ,∴
,∴ ,∴
,∴ .
.
(1)请你补全上面的证明过程;
(2)某广告设计需要在矩形的BC边上找到一个四等分点,请你仿照上面的方法,探究这个点的位置,在图上画出这个点,并说明理由.
25.(本小题满分12分)
某计算机商店销售计算机,现每台售价9000元时,每天销售20台,为了促销,经市场调查发现降价销售可使销量增加,若每台每降价300元,则日销量增加一台.设日销量增加 台时,日销售额为
台时,日销售额为 元.
元.
(1)用含 的代数式分别表示出日销售增加后每天的销量和每台计算机的售价;
的代数式分别表示出日销售增加后每天的销量和每台计算机的售价;
(2)写出 与
与 之间的函数关系式;
之间的函数关系式;
(3)如果你是计算机商店的经理,要使日销售额不低于促销前,那么降价后日销量增加的台数应确定在什么范围?并指出日销售额最大时每台计算机的售价应为多少?