2007-2008学年度菏泽市成武县第一学期期中考试
八年级数学试题
时间:120分钟 满分:120分
一、选择题:(每小题3分,共36分)
1.设圆的半径为R,周长为L,则R与L之间的关系式为L=2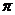 R,下面说法中正确的是( )
R,下面说法中正确的是( )
A.L、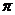 、R是变量,2是常量
B.L、R是变量,2、
、R是变量,2是常量
B.L、R是变量,2、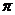 是常量
是常量
C.L、2是常量,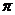 、R是变量 D.L、2、
、R是变量 D.L、2、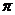 是常量,R是变量
是常量,R是变量
2.下列说法中正确的是 ( )
A.变量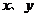 满足
满足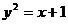 ,则y是
,则y是 的函数
的函数
B.变量a、b、c满足a=2b+c一1,则a是b和c的函数
C.变量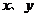 满足
满足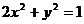 ,则y是
,则y是 的函数
的函数
D.变量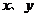 满足
满足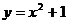 ,则y是
,则y是 的函数
的函数
3.关系式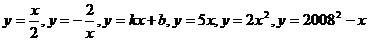 中,是一次函数的有 ( )
中,是一次函数的有 ( )
A.1个 B.2个 C.3个 D.4个
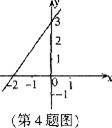
4.如图,一次函数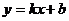 的图像经过A(0,3)和B(一2,0)两点,则
的图像经过A(0,3)和B(一2,0)两点,则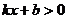 的解集为( )
的解集为( )
A.x>3 B.x>一2 C.x<3 D.x<一2
5.李老师骑自行车上班,最初以某一速度匀速行进,中途由于自行车发生故障,停下修车耽误了几分钟,为了按时到校,李老师加快了速度,仍保持匀速行进,结果准时到校,在课堂上,李老师请学生画出自行车行进路程s(km)与行进时间t(h)的函数图象的示意图.同学们画出的示意图有如下四种情况,你认为正确的是

A B C D
6.某班有50名学生,期中考试后,老师为了更清楚地表示数学成绩在每个分数段的人数占全班人数的百分比,应绘制 ( )
A.条形统计图 B.折线统计图 C.扇形统计图 D.直方图
7.八年级(1)班有48名学生,班长全面调查了全班同学的睡眠时间,并绘制了扇形统计图。其中“睡眠时间在8小时到8.5小时之间的学生人数的圆心角是60°,则下列说法正确的是 ( )
A.睡眠时间在8小时到8.5小时之间的学生人数占全班人数的60%
B.睡眠时间在8小时到8.5小时之间的学生有l2人
C.睡眠时间在8小时到8.5小时之间的学生最多
D.睡眠时间在8小时到8.5小时之间的学生人数占全班人数的
8.八年级(2)班有50名学生,一次数学测验,成绩落在80―89分之间的数据的频率是0.38.则成绩在80―89分之间的学生人数为 ( )
A.3 B.42 C.19 D.21
9.如图,∠l=∠2,AE=AB,添加下面条件不能使△AED≌△ABC的是 ( )
A.AD=AC B.ED=BC C.∠C=∠ADE D.∠B=∠E
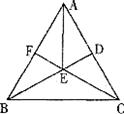
10.如图,△ABC中,AB=AC,AF=AD,则图中全等三角形共有 ( )
A.3对 B.4对 C.5对 D.6对
二、填空题:请将结果直接填在横线上(每小题4分,共32分)
11.若函数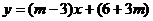 是一次函数,则m满足的条件是
;若此函数是正比例函数,则m满足的条件是
,此时,函数的解析式为
.
是一次函数,则m满足的条件是
;若此函数是正比例函数,则m满足的条件是
,此时,函数的解析式为
.
12.若y与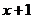 成正比例,且当
成正比例,且当 =2时,y=9,则当
=2时,y=9,则当 =4时,y=
.
=4时,y=
.
13.直线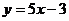 与直线
与直线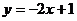 的交点坐标为
.
的交点坐标为
.
14.请写出一个一次函数的解析式,使它的图象经过点(0,4): .
15.本学期开学以来,你学习一直很努力,你的数学成绩逐步提高,为了让家长了解这种情况,你最好将开学以来几次数学测验的成绩用 统计图表示出来.
16.统计中常见的四种统计图是 、 、 、 .
17.如图,△ABD≌△CDB,∠ABD=40°,∠CBD=20°,则∠C= .

18.△ABC和△ADC中,下列三个论断:
(1)AB=AD (2) ∠BAC=∠DAC (3)BC=DC
将两个论断作为条件,另一论断作为结论,写出一个真命题
.
三、解答题(本题共7个小题,共58分)
19.(本题9分)如图甲是某中学某次“献爱心”自愿捐款活动学生捐款情况条形统计图,图乙是该中学学生人数比例分布图,该校共有学生l200人.
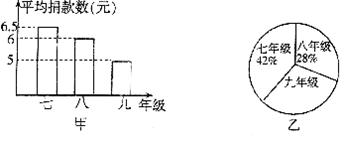
根据图示,求七、八、九年级学生各捐款多少元.
20.(本题8分)
下列数据是截止到2002年费尔兹奖得主获奖时的年龄:
29 39 35 33 39 28 33 35 31 31 37 32 38 36 31
39 32 38 37 34 29 34 38 32 35 36 33 29 32 35
36 37 39 38 40 38 37 39 38 34 33 40 36 36
若组距定为5,各组定为25≤ <30,30≤
<30,30≤ <35……,请列出频数分布表,并画出频数分布直方图.
<35……,请列出频数分布表,并画出频数分布直方图.
21.(本题8分)已知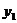 与
与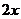 成正比例,
成正比例,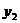 与
与 +1成正比例,
+1成正比例,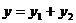 ,当
,当 =2时,y=9;当
=2时,y=9;当 =3时,y=14,求y与
=3时,y=14,求y与 的函数关系式.
的函数关系式.
22.(本题7分)已知直线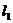 :
: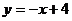 ,直线
,直线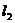 :y=3
:y=3 +6,求
+6,求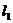 、
、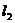 与
与 轴所围成的三角形的面积.
轴所围成的三角形的面积.
23.(本题l2分)我县为加快污水处理工程的进度,把两段长度相等的修建任务分别交给甲、乙两个工程队同时进行修建,如图是反映修建长度y(米)与修建时间 (时)之间关系的部分图象,请根据图象解答下列问题:
(时)之间关系的部分图象,请根据图象解答下列问题:
(1)写出甲队在0≤ ≤6的时段内,y与
≤6的时段内,y与 之间的函数关系式;
之间的函数关系式;
(2)写出乙队在2≤ ≤6的时段内,y与
≤6的时段内,y与 之间的函数关系式;
之间的函数关系式;
(3)施工几小时后,甲队所修的长度开始超过乙队;
(4)请你给乙队提一条合理化建议.

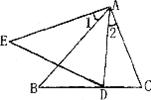
24.(本题6分)如图,D、E分别是等边△ABC的边AC、BC上的点.请问当D、E满足什么条件时,BD=AE,试说明理由.

25.(本题8分)如图,在△ABC中,AB=AC,且∠BAC=90°,DE过点A,且CE⊥DE,BD⊥DE.求证ED=EC+BD.
