1．-3的倒数是       ，-|-2|=       。

2．已知最简二次根式与是同类二次根式，则x=      ．

3．分解因式2m²-4mx+2m=           ．

4．如图，A是反比例函数的图像上一点，已知Rt△AOB的面积为3，则k=     ．

5．已知一个三角形的边长满足x²-6x+8=0,则这个三角形周长为          ．

6．三条直线最多能组成        个直角．

7．下列结论正确的是

A． 2a+3b-5ab          B． （10⁴）²=10¹⁶

C． a⁰=1                     D．-0．00120写成科学记数法的形式为-1．20×10^-3

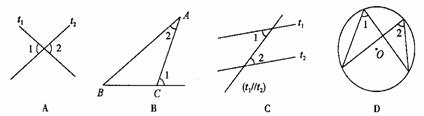
8．图中能够说明∠1>∠2的是

9．王老师对刘涛同学中考前的3次模拟考试数学成绩进行统计分析，判断刘涛同学的数学成绩是否稳定，王老师需要知道刘涛的这三次数学成绩的

A．平均数                    B．方差                      C．中位数                   D．无法确定

10．化简的结果是          ．

A．              B．         C． 0                        D．无法确定

11．下图中的主视图和俯视图对应的物体是

12．小明根据邻居家的故事写了一首小诗：“儿子学成今日返，老父早早到车站，儿子到后细端详，父子高兴把家还。”如果用纵轴y表示父亲与儿子进行离家的距离，用横轴x表示父亲离家的时间，那么下面的图像与上述诗的含义大致吻合的是

13．下列说法不正确的是

A． 单项式-3⁴a²ⁿb¹⁵的次数高于4²a⁵b⁴ⁿ的次数，则正整数n的值有5个

B． 近似数23．50有三个有效数字，分别为2，3，5

C． x^-1,都是分式

D．将点p（3，1）绕原点O按顺时针方向旋转90°到点Q，则点Q的坐标为（1，-3）

14．下列说法正确的是

A． “买一张体育彩票中奖”是属于确定事件

B． 函数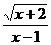中自变量x的取值范围是x≥-2或x≠1

C． 一个圆在平面上的平行投影可能是圆，也可能是椭圆或线段

D． 对于任何实数x、y多项式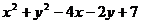的值不小于2

15．下列错误的是

A． 在半径为5的圆O中，弦AB=6cm，弦CD=8cm，且AB∥CD,则AB与CD之间的距离为7cm

B． 已知四个函数①y=-4x，②y=x-3，③y=④，其中y随x的增大而减小的函数有3个

C． 在Rt△ABC中，若BC=6，AC=8, 则cosB=

16．（本题满分6分）为了了解初三毕业班学生一分钟跳绳次数的情况，某校抽取了一部分初三毕业进行一分钟跳绳次数的测试，将所得数据进行处理，可得斌率分布表。

组别

分组

频数

频率

1

89．5～99．5

4

0．04

2

99．5～109．5

3

0．03

3

109．5～119．5

46

0．46

4

119．5～129．5

b

c

5

129．5～139．5

6

0．06

6

139．5～149．5

2

0．02

合计

a

1．00

（1）这个问题中，总体是                       ，样本容量a=            ；

（2）第四小组的频数b=              ，频数c=            ；

（3）若次数在110次（含110次）以上为达标，试估计该校初三毕业生一分钟跳绳次数的达标率是多少？

（4）在这次测试中，学生跳绳次数的中位数落在哪个小组内？

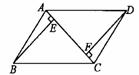
17．（本题满分6分）如图在□ABCD中，BE⊥AC于点E，DF⊥AC点F,求证：AE=CF．

18．（本题满分7分）有两个可以自由转动的均匀转盘A、B被分成了3等份，并在每份内均标有数字，如图所示，规则如下：①分别转动转盘A、B；②两个转盘停止后，将两个指针所指份内的数字相乘（若指针在等分线上，那么重转一次，直到指针指向某一份为止）．

（1）用列表法（或树形图）分别求出数字之积为3的倍数和数字之积为5的倍数的概

（2）小明和小亮想用两个转盘做游戏，他们规定：数字之积为3的倍数时，小明得2分；数字之积为5的倍数时，小亮得3分，这个游戏对双方公平吗？请说明理由；以为不公平的，试修改得分规定，使游戏对双方公平。

19．（本题满分7分）如图，已知点O为Rt△ABC斜边AB上一点，以O为圆心，OA为半径的圆与BC相切与点D，与AB相交于点E。（1）试判断AD是否平分∠BAC?并说明理由；（2）若BD=3BE,CD=3,求?O的半径。

20．（本题满分8分）谋单位需以：“挂号信”或“特快专递”方式向五所学校各寄一封信，这五封信的重量分别为75g，90g，250g，340g，400g。根据这五所学校的地址及信件的重量的范围，在邮局查得相关邮费标准如下：

业务种类

计费单位

资费标准（元）

挂号费（元/封）

特制信封（元/个）

挂号信

首重100g内，每重20g

0．8

3

3

0．5

续重101-2000g，每重100g

2．00

特快专递

首重1000g内

5

3

1．0

（1）重量为90g的信以“挂号信”方式寄出，邮寄费为多少元？若以“特快专递”方式寄出呢？

（2）这五封信分别以怎样的方式寄出最合算？请说明理由。

21． （本题满分8分）黄冈实验中学以促校园文化环境来带动教学质量的提升，学校想在校园一角的荒地处改建一个梅园，种植品种各样的梅花，荒地两边是互相垂直的墙，如图所示，经过测量，梅园另两边想用长30cm的装饰栏杆围成，现在全校学生中征集了三幅不同的设计图案，如图（1）（2）（3）．

（1）通过计算，比较S₁,S₂,S₃的大小（结果保留一位小数）

（2）请你设计出一种图案，使其面积最大，并在图中标出有关数据，求出其面积。（结果保留一位小数）

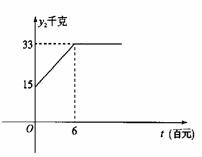
22． （本题满分10分）茶农张大爷种有茶树共50亩，其中丘陵地20亩，山地30亩，每亩丘陵地产量y₁（千克）与投资x（百元）之间的函数关系式为：

每亩山地产量y₁（千克）与投资x（百元）之间的关系如图所示，张大爷现在总投资金240（百元）。

（1）试求张大爷每亩丘陵山地投资600元和每亩山地投资600元时茶叶的总产量分别是多少千克？

（2）写成张大爷家茶叶总产量（千克）与丘陵地每亩投资x（百元）之间的函数关系式，并指出x的取值范围；

（3）当x取何值时，茶叶的总产量最高？最高产量为多少千克？

23． （本题满分14分）已知抛物线y=ax²+bx+c与y轴交于点A（0，3），与x轴分别交于B（1，0），C（5，0）两点。

（1）求此抛物线的解析式；

（2）若点D为线段OA的一个三等分点，求直线DC的解析式；

（3）若一个动点P自OA的中点M出发，先到达x轴上的某点（设为点E），再到达抛物线的对称轴上某点（设为点F），最后运动到点A，求使点P运动的总路径最短的点E，点F的坐标，并求出这个最短总路径的长。

（4）若点N的坐标为（3，4），Q为坐标轴上一点，△ONP为等腰三角形，请直接写出点Q的坐标。