2007-2008学年度云南省华宁一中九年级上学期期末测试
数学试题
一、填空题:(每题3分,共30分)
1.如果一个菱形的一条对角线的长为
2.在10张卡片上分别写有0至9十个数字,将它们放入纸箱后,任意摸出一张,则摸到数字2 的概率为 .
3.若反比例函数y=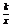 的图象经过点(3,-4),则此函数的表达式是
。
的图象经过点(3,-4),则此函数的表达式是
。
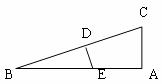
4.如图在△ABC中∠A=90o,∠B=30o,DE垂直平分BC,垂足为D,交AB于E,AC=
5.请你编写一个有一个根是-5的一元二次方程 。
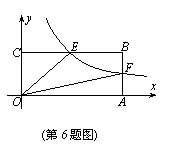
6.如图,已知双曲线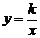 (x>0)经过矩形OABC边AB的中点F,交BC于点E,且四边形OEBF的面积为2,则k=______________。
(x>0)经过矩形OABC边AB的中点F,交BC于点E,且四边形OEBF的面积为2,则k=______________。
7.放学后,小明和小颖按如下规则做游戏:桌面上放有5支铅笔,每次取1支或2支,由小明先取,最后取完铅笔的人数获胜。如果小明获胜的概率为1,那么,小明第一次应该取走 支。
8.同时抛掷两枚均匀的硬币,则两枚硬币正面都向上的概率是 。
9.有一间长 ,四周未铺地毯的留空宽度相同,则留空的宽度是
。
,四周未铺地毯的留空宽度相同,则留空的宽度是
。
10.某个体户以50000元的资金经商,在第一年中获得一定利润,已知这50000元资金加上第一年的利润一起在第二年共得利润2612.50元,而且第二年的利润比第一年的利润多0.5%,则第一年的利润是 元。
二、选择题:(每题3分,共30分)
12.如果2是一元二次方程x2=c的一个根,那么常数c是 ( )
A.2 B.-
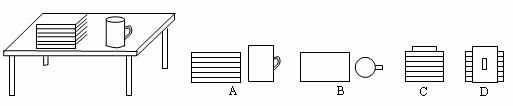
13.如图,桌上放着一摞书和一个茶杯,从正面看的图形是( )
14.下列说法正确的有( )个
(1)对于反比例函数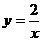 ,(x1,y1),(x2,y2)是其图象上两点,若x1<x2,则y1>y2;
,(x1,y1),(x2,y2)是其图象上两点,若x1<x2,则y1>y2;
(2)对角线互相垂直平分的四边形菱形;
(3) 一组对边平行的四边形是梯形;
(4) 是反比例函数;
是反比例函数;
(5)若一个等腰三角形的两边长为2和3,那么它的周长为7.
A.2
B.
15.将一元二次方程式x2-6x-5=0化成(x+a)2=b的形式,则b= ( )
A. -4 B.
16.下列四个几何体中,主视图、左视图与俯视图是全等图形的几何体是 ( )
A.球 B.圆柱 C.三棱柱 D.圆锥
17.设有12只型号相同的杯子,其中一等品7只,二等品3只,三等品2只,则从中任取一只,是二等品的概率等于 ( )
A.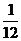 B.
B. C.
C.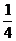 D.
D.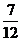
18.如图,四边形ABCD是矩形,F是AD上一点,E是CB延长线上一点,且四边形AECF是等腰梯形.下列结论中不一定正确的是 ( )

A.AE=FC B.AD=BC C.∠AEB=∠CFD D.BE=A
19.小明外出游玩,带上棕色、兰色、淡黄色3件上衣和兰色、白色2条长裤,他任意
拿出1件上衣和1条长裤正好是棕色上衣和兰色长裤的概率是 ( )
A. B.
B. C.
C. D.
D.
20.小刚与小亮一起玩一种转盘游戏。如图是两个完全相同的转盘,每个转盘分成面积相等的三个区域,分别用“

A.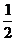 B.
B.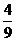 C.
C. D.
D.
21.近几年,某市在经济建设中取得突出成就,2004?2006年三年该市的国内生产总值的和为2200亿元。图甲是这三年该市的国内生产总值的扇形统计图,图乙是这三年该市总人口折线统计图。根据以上信息,下列判断:①2006年该市国内生产总值超过800亿元;②2006年该市人口的增长率比2005年人口的增长率低;③2006年比2004年该市人均国内生产总值增加 万元;④如果2007年该市人口的年增长率与2006年人口的年增长率相同,且人均国内生产总值增长10%,那么2007年全市的国内生产总值将为
万元;④如果2007年该市人口的年增长率与2006年人口的年增长率相同,且人均国内生产总值增长10%,那么2007年全市的国内生产总值将为 亿元。其中正确的只有(
)
亿元。其中正确的只有(
)
A.①②④ B.①③④ C.②③ D.①③

三、解答题:(每题10分,共60分)
22.如图所示的图象所描述的是一辆小汽车沿一条高速公路行驶过程的图象,根据图象所提供的信息回答下列问题:

(1)求出速度v与t之间的函数关系式并指出这条高速公路的全长是多少?
(2)汽车的最大速度可以达到多少?
(3)汽车最慢用几小时可以达到?如果在3小时以内到达,汽车的速度应该不少于多少?
23.已知关于x的一元二次方程x2-(k+1) x-6=0的一个根是2,求方程的另一根和k的值.
24.“便民”水泥代销点销售某种水泥,每吨进价为250元.如果每吨销售价定为290元时,平均每天可售出16吨.
(1)若代销点采取降低促销的方式,试建立每吨的销售利润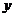 (元)与每吨降低
(元)与每吨降低 (元)之间的函数关系式.
(元)之间的函数关系式.
(2)若每吨售价每降低5元,则平均每天能多售出4吨.问:每吨水泥的实际售价定为多少元时,每天的销售利润平均可达720元.
25.如图,在△ABC中∠BCA=90°,D.E分别是AC.AB边的中点,F在BC的延长线上。∠CDF=∠A。求证:四边形DECF是平行四边形。

6.图2是中国象棋棋盘的一部分,图中红方有两个马,黑方有三个卒子和一个炮,按照中国象棋中马的行走规则(马走日字,例如:按图1中的箭头方向走),红方的马现在走一步能吃到黑方棋子的概率是多少?

27.如图,反比例函数y= 在第一象限内的图象上有A.B两点,横坐标分别为m、n,直线AB与x轴y轴分别交于点C.D,作AE⊥y轴于E,SF⊥x轴于F。
在第一象限内的图象上有A.B两点,横坐标分别为m、n,直线AB与x轴y轴分别交于点C.D,作AE⊥y轴于E,SF⊥x轴于F。
求证:△FADE≌△CBF
