2007年11月临沂市沂水县八年级数学定时作业
一、选择题:下列各题所给四个选项只有一个是正确的,请将正确选项的代号涂在答题卡上或填写在下列答题框内。(每小题4分,共32分)
1.下列给出的函数中,是正比例函数的是
(A) (B)
(B) (
( ,
, 为常数)
为常数)
(C) (D)
(D)
2.对于函数关系式 ,下列说法错误的是
,下列说法错误的是
(A) 、
、 都是变量
(B)
都是变量
(B) 是
是 的函数
的函数
(C) 也是
也是 的函数 (D)
的函数 (D) 的取值范围是任意实数,
的取值范围是任意实数,
3.正比例函数 (
( )的图像经过第二、四象限,则
)的图像经过第二、四象限,则
(A) 随
随 增大而减小
增大而减小
(B) 随
随 增大而增大
增大而增大
(C)当 时,
时, 随
随 增大而增大;当
增大而增大;当 时,
时, 随
随 增大而减小
增大而减小
(D)不论 值如何变化,
值如何变化, 值不变
值不变
4.如图,将直线 向上平移3个单位得到直线
向上平移3个单位得到直线 ,则
,则 的解析表达式为
的解析表达式为

(A)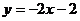 (B)
(B)
(C)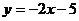 (D)
(D)
5.不能确定两个三角形全等的条件是
(A)三条边对应相等
(B)两条边及其夹角对应相等
(C)两角和一条边对应相等
(D)两条边和其中一条边所对的角对应相等
6.已知函数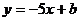 上三点A(-1,
上三点A(-1,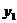 )、B(-3,
)、B(-3, )、C(2,
)、C(2,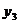 )
)
(A)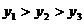 (B)
(B)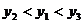
(C) (D)
(D)
7.在Rt△ABC和 中,
中,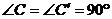 ,
, ,
, ,则下列结论正确的是
,则下列结论正确的是
(A) (B)
(B)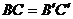
(C)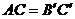 (D)
(D)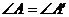
8.如图,若OA=OB,点C在OA上,点D在OB上,OC=OD,AD与BC相交于E,则图中全等三角形共有
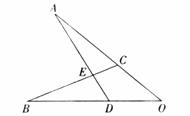
(A)1对 (B)2对 (C)3对 (D)4对
二、填空题:将正确的结果直接填在题中的横线上。(每小题4分,共32分)
9.陈村2006年的年总收入为800万元,当这个村人口数 变化时,该村的人均年收入P也发生变化,P=
。(
变化时,该村的人均年收入P也发生变化,P=
。( 为正整数)
为正整数)
10.直线 的图像与
的图像与 轴交于点(?2,0),当
轴交于点(?2,0),当 时,
时, 的取值范围是
。
的取值范围是
。

11.如图,在△AED和△BFC中,AF=BE,AD=BC,当添加条件 时,就有△AED≌△BFC。(只需填写一个你认为正确的条件即可)

12.在△ABC中,∠ABC=∠ACB,BD平分∠ABC交AC于D,若∠CDB=150°,则∠A= 0。
13.已知: ,
, ,当
,当 时,
时, 的取值范围是 。
的取值范围是 。
14.甲、乙两地间相距 (千米)与行驶的时间
(千米)与行驶的时间 (小时)之间的函数关系式为 。
(小时)之间的函数关系式为 。
15.某公司销售人员的个人月收入与其每月的销售量成一次函数关系,图像如图所示,则此销售人员的销售量为3千件时的月收入是 元。

16.如图,已知在△ABC中,AD平分∠BAC,AB+BD=AC,则∠B┱∠C= 。
三、证明题:本大题共两小题,共19分。
17.满分9分。
已知:如图,AB∥CD,F是AC的中点,求证:F是DE的中点。


18.满分10分。
如图,在△ABC和△ABD中,现给出如下三个论断:
①AD=BC;②∠C=∠D;③∠1=∠2。
请选择其中两个论断为条件,另一个论断为结论,构造一个命题。
(1)写出所有的真命题;(写成“若 , ,则 ”的形式,可用序号表示)
(2)请选择一个真命题证明。
你选择的真命题是:若 , ,则 。
四、解答题:本大题共3小题,共37分。
19.满分10分。
下面是某一年参加国际教育评估的20个国家学生的数学平均成绩( )的扇形统计图,试根据扇形统计图中的信息,在给定的坐标纸上画出这一统计结果的频数分布直方图,并回答下列问题:
)的扇形统计图,试根据扇形统计图中的信息,在给定的坐标纸上画出这一统计结果的频数分布直方图,并回答下列问题:


(1)哪一个图能很好地说明一半以上国家的学生成绩在 之间?
之间?
(2)哪一个图能更好地说明学生成绩在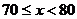 的国家多于在
的国家多于在 的国家?
的国家?
20.满分10分。
某地举办乒乓球比赛的费用 (元)包括两部分:一部分是租用比赛场地固定不变的费用
(元)包括两部分:一部分是租用比赛场地固定不变的费用 (元),另一部分与参加比赛的人数
(元),另一部分与参加比赛的人数 (人)成正比例,当
(人)成正比例,当 时,
时, ,当
,当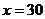 时,
时, 。
。
(1)求 与
与 之间的函数关系式;
之间的函数关系式;
(2)如果有50名运动员参加比赛,且全部费用由运动员分摊,那么每名运动员需要支付多少元?
21.满分15分。
小张骑车往返于甲、乙两地,距甲地的路程 (km)与时间
(km)与时间 (h)的函数图像如图所示。
(h)的函数图像如图所示。

(1)小张在路上停留 h,他从乙地返回时骑车的速度为 km/h。
(2)小李与小张同时从甲地出发,按相同路线匀速前往乙地,到乙地停止,途中小李与小张共相遇3次,请在图中画出小李距甲地的路程 (km)与时间
(km)与时间 (h)的函数的大致图像。
(h)的函数的大致图像。
(3)小王与小张同时出发,按相同路线前往乙地,距甲地的路程 (km)与时间
(km)与时间 (h)的函数关系式为
(h)的函数关系式为 。小王与小张在途中共相遇几次?请你计算第一次相遇的时间。
。小王与小张在途中共相遇几次?请你计算第一次相遇的时间。