2006-2007学年度浙江省宁波市镇海区第一学期期末考试测试
八年级数学试题
温馨提示:试卷共8页,有三大题,25小题,2道附加题。考试时间100分钟,满分l00分。请仔细审题,细心答题,相信你一定会有出色的表现!
一、选择题(每小题3分,共30分。每小题只有一个选项是正确)
1.如图1,已知 ,
,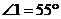 ,则
,则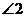 的大小是 ( )
的大小是 ( )
A、35° B、125° C、145° D、55°


2.平面直角坐标系中,点P(1,4)在 ( )
A、第一象限 B、第二象限
C、第三象限 D、第四象限
3.如图是一个水管的三叉接头,它的左视图是 ( )

4.下列运算正确的是 ( )
A、 B、
B、
C、 D、
D、
5.如图,在等腰三角形ABC中,AB=AC,CD⊥AB,垂足为D, ,则∠BCD=(
)
,则∠BCD=(
)
A、30° B、20° C、70° D、60°

6.三项调查:①了解一批炮弹的杀伤半径;②检查小锋作业中的20道化简题是否存在错误;③考查中国国民对环境的保护意识。其中不适合作普查而适合作抽样调查的个数是( ) A、0 B、l C、2 D、3
7.如下图表示关于 的一个不等式组的解,这个不等式的解是 ( )
的一个不等式组的解,这个不等式的解是 ( )

A、 B、
B、 或
或
C、 D、
D、
8.若将如图的立方体表面展开图折叠成立方体后,图中的“乐”所对的面是( )

A、“祝” B、“新” C、“年” D、“快”
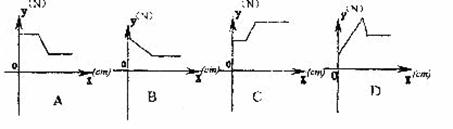
9.在实验课上,小明用弹簧称将铁块A悬于盛有水的水槽中,然后匀速向上提起,直至铁块完全露出水面一定高度,则下图能反映弹簧称的读数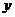 (单位N)与铁块被提起的高度
(单位N)与铁块被提起的高度 (单位cm)之间的函数关系的大致图像是 ( )
(单位cm)之间的函数关系的大致图像是 ( )

10.自

A、0.504亿元 B、50.4亿元 C、58.4亿元 D、62.4亿元
二、填空题(每小题3分,共24分)
11.要使二次根式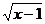 有意义,字母
有意义,字母 的取值范围是___________。
的取值范围是___________。
12.如图所示,相框一边AB长为 ,则相框的支架CD长为___________cm。
,则相框的支架CD长为___________cm。

13.某班10位N学将平时积攒的零花钱捐献给贫困地区的失学儿童。每人捐款金额(单位:元)依次为:l0,12,20,14,15,12,16,18,12,15。捐款金额的中位数是___________元,众数是___________元。
14.一次函数数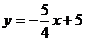 与
与 轴的交点坐标为___________。
轴的交点坐标为___________。
15.如图:CD平分∠ACB,DE∥AC且∠1=20°,则∠2=___________度。


16.如图,是象棋盘的一部分,若“帅”位于点(2,-l)上,,“相”位于点(4,-l)上,则“炮”所在的点的坐标是___________。
17.对于整数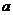 ,
,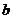 ,
, ,
, ,符号
,符号 表示运算
表示运算 ,已知,
,已知,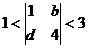 ,则
,则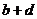 的值是___________。
的值是___________。
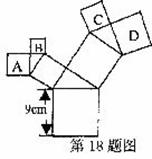
18.如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边和长为
三、解答题
19.计算(每小题4分,共8分)
(1)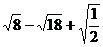
(2)
20.解不等式(组):(每小题4分,共8分)
(1)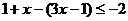
(2)
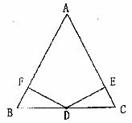
21.(本题6分)如图,已知D是△ABC的BC边的中点,DE⊥AC,DF⊥AB,垂足分别为E,F,且DF=DE,则△ABC是等腰三角形吗?请说明理由。
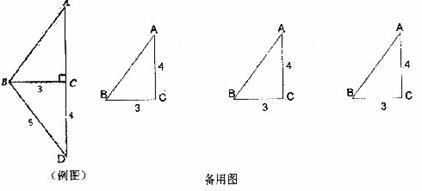
22.(本题6分)已知Rt△ABC中,∠C=90°,AC=4,BC=3。在Rt△ABC的外部拼接一个合适的直角三角形,使得拼成的图形是一个等腰三角形,如例图所示。请你用铅笔与尺子在备用图中分别画出三种与示例不同的拼接方法,并在图中标明拼接的直角三角形的三边长。
23.(本题8分)如图
(1)将△ABC向上平移2个单位,再向右平移2个单位,画出所得的像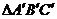 ,并求出三顶点的坐标。
,并求出三顶点的坐标。
(2)将△ABC以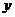 轴为对称轴作一次轴对称交换,画出所得的像
轴为对称轴作一次轴对称交换,画出所得的像 ,并写出经变换后
,并写出经变换后 各顶点的坐标。
各顶点的坐标。
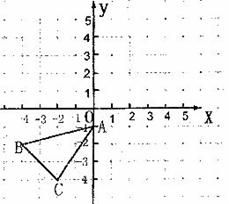
24.(本题l0分)如图甲所示,A、B两个旅游点从2002年至2006年“五一”黄金周的游客人数变化情况分别用实线和虚线表示。根据图中所示解答以下问题:
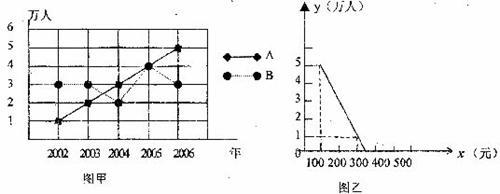
(1)分别求A、B两个旅游点从2002到2006年“五一”黄金周的游客人数的平均数和方差并从平均数和方差的角度,用一句话对这两个旅游点的情况进行评价;
(2)为保护旅游点环境和游客的安全,A、B旅游点“五一”黄金周的游客人数都不能超过4万人。
①A旅游点决定2007年起以提高门票价格来控制游客数量。经市场预测,绘制游客人数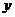 (万人)与门票价格
(万人)与门票价格 (元)函数图像如图乙所示。求游客人数
(元)函数图像如图乙所示。求游客人数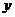 (万人)与门票价格
(万人)与门票价格 (元)的函数关系式。
(元)的函数关系式。
②B旅游点计划投入80万元引进一项游乐设施,预计开放后07年“五一”黄金周的游客数比上年有所增加,且其中6成的游客会参加此项游乐活动。若07年B旅游点门票保持06年相同价格120元/人,而该游乐项目每人需加收20元,已知该游乐设施每100个游客参加就要多投入管理维修等费用200元,假设B旅游点其他设施管理等投入与06年保持不变,那么在保护旅游点环境和游客的安全的前提下,对07年“五一”黄金周来说,该景点扣除投资和管理维修费用后的纯收益能否超过上年?若能,求出07年游客数比上年增长的百分率范围;若不能,请说明理由。(百分率精确到1%)
附加题:(不计总分,考生自己决定是否选做,具体由各校自行处理)
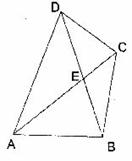
1.(10分)如图所示,在四边形ABCD中,对角线AC与BD相交于点E,若AC平分∠BAD,且AB=AE,AC=AD。对于下列结论:
①AB⊥BC ②DC=DE ③ 哪些是正确的,哪些是错误的?若是正确的请说明理由。
哪些是正确的,哪些是错误的?若是正确的请说明理由。
2.(10分)一只青蛙在平面直角坐标系上从点(1,1)开始,可以按照如下两种方式跳跃:
①能从任意一点(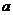 ,
,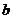 ),跳到点(
),跳到点(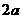 ,
,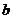 )或(
)或(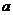 ,
,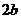 );
);
②对于点(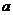 ,
,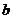 ),如果
),如果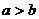 ,则能从(
,则能从(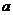 ,
,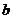 )跳到(
)跳到( ,
,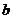 );如果
);如果 ,则能从(
,则能从(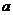 ,
,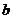 )跳到(
)跳到(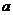 ,
,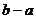 )。
)。
例如,按照上述跳跃方式,这只青蛙能够到达点(3,1),跳跃的一种路径为:
(1,1)→(2,1)→(4,1)→(3,1)
请你思考:这只青蛙按照规定的两种方式跳跃,能到达下列各点吗?如果能,请分别给出从点(1,1)出发到指定点的路径;如果不能,请说明理由。
(1)(3,5);
(2)(12,60)