2007年江西省中等学校招生考试
数学试卷(课标卷)
说明:本卷共有六个大题,25个小题,全卷满分120分,考试时间120分钟.
一、填空题(本大题共10小题,每小题3分,共30分)
1.计算: .
.
2.化简: .
.
3.在“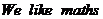 .”这个句子的所有字母中,字母“
.”这个句子的所有字母中,字母“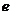 ”出现的频率约为
(结果保留2个有效数字).
”出现的频率约为
(结果保留2个有效数字).
4.在 中,
中,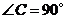 ,
, 分别是
分别是 的对边,若
的对边,若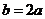 ,则
,则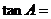 .
.

5.在加油站,加油机显示器上显示的某一种油的单价为每升4.75元,总价从0元开始随着加油量的变化而变化,是总价 (元)与加油量
(元)与加油量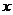 (升)的函数关系式是 .
(升)的函数关系式是 .
6.在数轴上与表示 的点的距离最近的整数点所表示的数是
.
的点的距离最近的整数点所表示的数是
.
7.如图,在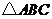 中,点
中,点 是
是 上一点,
上一点,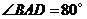 ,
, ,则
,则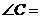
度.

8.如图,点 是⊙O上两点,
是⊙O上两点, ,点
,点 是⊙O上的动点(
是⊙O上的动点( 与
与 不重合),连结
不重合),连结 ,过点
,过点 分别作
分别作 于
于 ,
, 于
于 ,则
,则 .
.

9.已知二次函数 的部分图象如图所示,则关于
的部分图象如图所示,则关于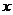 的一元二次方程
的一元二次方程 的解为
.
的解为
.

10.如图,已知 ,点
,点 在
在 边上,四边形
边上,四边形 是矩形.请你只用无刻度的直尺在图中画出
是矩形.请你只用无刻度的直尺在图中画出 的平分线(请保留画图痕迹).
的平分线(请保留画图痕迹).

每小题只有一个正确选项,请把正确选项的代号填在题后的括号内.
二、选择题(本大题共6小题,每小题3分,共18分)
11.在某次国际乒乓球单打比赛中,甲、乙两名中国选手进入最后决赛,那么下列事件为必然事件的是( )
A.冠军属于中国选手 B.冠军属于外国选手
C.冠军属于中国选手甲 D.冠军属于中国选手乙
12.对于反比例函数 ,下列说法不正确的是( )
,下列说法不正确的是( )
A.点 在它的图象上 B.它的图象在第一、三象限
在它的图象上 B.它的图象在第一、三象限
C.当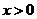 时,
时, 随
随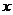 的增大而增大 D.当
的增大而增大 D.当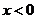 时,
时, 随
随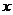 的增大而减小
的增大而减小
13.下列图案中是轴对称图形的是( )

14.已知: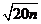 是整数,则满足条件的最小正整数
是整数,则满足条件的最小正整数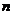 为( )
为( )
A.2 B.
15.桌面上放着1个长方体和1个圆柱体,按如图所示的方式摆放在一起,其左视图是( )

16.如图,将矩形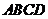 纸片沿对角线
纸片沿对角线 折叠,使点
折叠,使点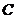 落在
落在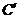 处,
处,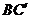 交
交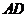 于
于 ,若
,若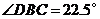 ,则在不添加任何辅助线的情况下,图中
,则在不添加任何辅助线的情况下,图中 的角(虚线也视为角的边)有( )
的角(虚线也视为角的边)有( )

A.6个 B.5个 C.4个 D.3个
三、(本大题共3小题,第17小题6分,第18、19小题各7分,共20分)
17.计算: .
.
18.化简:
19.如图,在正六边形 中,对角线
中,对角线 与
与 相交于点
相交于点 ,
, 与
与 相交于点
相交于点 .
.
(1)观察图形,写出图中两个不同形状的特殊四边形;
(2)选择(1)中的一个结论加以证明.

四、(本大题共2小题,每小题8分,共16分)
20.某学校举行演讲比赛,选出了10名同学担任评委,并事先拟定从如下4个方案中选择合理的方案来确定每个演讲者的最后得分(满分为10分):
方案1 所有评委所给分的平均数.
方案2 在所有评委所给分中,去掉一个最高分和一个最低分,然后再计算其余给分的平均数.
方案3 所有评委所给分的中位数.
方案4 所有评委所给分的众数.
为了探究上述方案的合理性,先对某个同学的演讲成绩进行了统计实验.下面是这个同学的得分统计图:

(1)分别按上述4个方案计算这个同学演讲的最后得分;
(2)根据(1)中的结果,请用统计的知识说明哪些方案不适合作为这个同学演讲的最后得分.
21.如图,在 中,
中, ,
,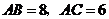 .若动点
.若动点 从点
从点 出发,沿线段
出发,沿线段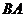 运动到点
运动到点 为止,运动速度为每秒2个单位长度.过点
为止,运动速度为每秒2个单位长度.过点 作
作 交
交 于点
于点 ,设动点
,设动点 运动的时间为
运动的时间为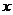 秒,
秒, 的长为
的长为 .
.
(1)求出 关于
关于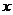 的函数关系式,并写出自变量
的函数关系式,并写出自变量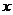 的取值范围;
的取值范围;
(2)当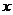 为何值时,
为何值时, 的面积
的面积 有最大值,最大值为多少?
有最大值,最大值为多少?

五、(本大题共2小题,第22小题8分,第23小题9分,共17分)
22.在一次数学活动中,黑板上画着如图所示的图形,活动前老师在准备的四张纸片上分别写有如下四个等式中的一个等式:
① ②
② ③
③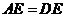 ④
④
小明同学闭上眼睛从四张纸片中随机抽取一张,再从剩下的纸片中随机抽取另一张.请结合图形解答下列两个问题:
(1)当抽得①和②时,用①,②作为条件能判定 是等腰三角形吗?说说你的理由;
是等腰三角形吗?说说你的理由;
(2)请你用树状图或表格表示抽取两张纸片上的等式所有可能出现的结果(用序号表示),并求以已经抽取的两张纸片上的等式为条件,使 不能构成等腰三角形的概率.
不能构成等腰三角形的概率.
23.2008年北京奥运会的比赛门票开始接受公众预订.下表为北京奥运会官方票务网站公布的几种球类比赛的门票价格,某球迷准备用8000元预订10张下表中比赛项目的门票.
(1)若全部资金用来预订男篮门票和乒乓球门票,问他可以订男篮门票和乒乓球门票各多少张?
(2)若在现有资金8000元允许的范围内和总票数不变的前提下,他想预订下表中三种球类门票,其中男篮门票数与足球门票数相同,且乒乓球门票的费用不超过男篮门票的费用,求他能预订三种球类门票各多少张?
比赛项目
票价(元/场)
男篮
1000
足球
800
乒乓球
500
六、(本大题共2小题,第24小题9分,第25小题10分,共19分)
24.在同一平面直角坐标系中有6个点: ,
, ,
, .
.
(1)画出 的外接圆⊙P,并指出点
的外接圆⊙P,并指出点 与⊙P的位置关系;
与⊙P的位置关系;
(2)若将直线 沿
沿 轴向上平移,当它经过点
轴向上平移,当它经过点 时,设此时的直线为
时,设此时的直线为 .
.
①判断直线 与⊙P的位置关系,并说明理由;
与⊙P的位置关系,并说明理由;
②再将直线 绕点
绕点 按顺时针方向旋转,当它经过点
按顺时针方向旋转,当它经过点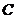 时,设此时的直线为
时,设此时的直线为 .求直线
.求直线 与⊙P的劣弧
与⊙P的劣弧 围成的图形的面积(结果保留
围成的图形的面积(结果保留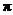 ).
).

25.实验与探究
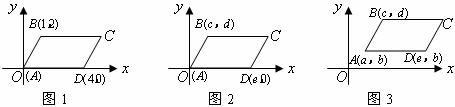
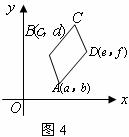
(1)在图1,2,3中,给出平行四边形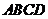 的顶点
的顶点 的坐标(如图所示),写出图1,2,3中的顶点
的坐标(如图所示),写出图1,2,3中的顶点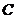 的坐标,它们分别是
的坐标,它们分别是 , ,
;
, ,
;
(2)在图4中,给出平行四边形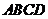 的顶点
的顶点 的坐标(如图所示),求出顶点
的坐标(如图所示),求出顶点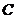 的坐标(
的坐标( 点坐标用含
点坐标用含 的代数式表示);
的代数式表示);
归纳与发现
(3)通过对图1,2,3,4的观察和顶点 的坐标的探究,你会发现:无论平行四边形
的坐标的探究,你会发现:无论平行四边形 处于直角坐标系中哪个位置,当其顶点坐标为
处于直角坐标系中哪个位置,当其顶点坐标为 (如图4)时,则四个顶点的横坐标
(如图4)时,则四个顶点的横坐标 之间的等量关系为
;纵坐标
之间的等量关系为
;纵坐标 之间的等量关系为
(不必证明);
之间的等量关系为
(不必证明);
运用与推广
(4)在同一直角坐标系中有抛物线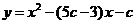 和三个点
和三个点 ,
,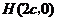 (其中
(其中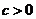 ).问当
).问当 为何值时,该抛物线上存在点
为何值时,该抛物线上存在点 ,使得以
,使得以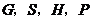 为顶点的四边形是平行四边形?并求出所有符合条件的
为顶点的四边形是平行四边形?并求出所有符合条件的 点坐标.
点坐标.