牡丹江名校调研系列卷?九年级月考(三)
数学(人教新课标版)
一、填空题(每小题2分,共20分)
1.如果 =
=
2.观察下列各式: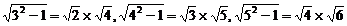 ……试猜想
……试猜想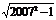 =
=
3.如图所示,分别以n边形的顶点为圆心,以单位1为半径画圆,则图中阴影部分的面积之和为 个平方单位。
4.若一元二次方程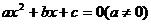 有一根是1,则a+b+c=
有一根是1,则a+b+c=
5.已知代数式 与代数式9x-9的值相等,则x=
与代数式9x-9的值相等,则x=
6.如图,正方形ABCD的边长为
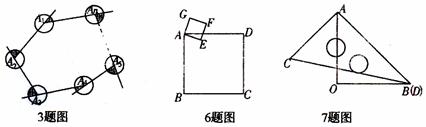
7.一副三角板按如图所示叠放在一起,若固定△AOB,将△ACD绕着公共顶点A,按顺时针方向旋转α度(0<α<180),当△ACD的边CD与△AOB的边AB平行时,相应的旋转角α的值是
8.已知圆A和圆B相切,两圆的圆心距为
cm.
9.如图,已知BC的等腰三角形纸片ABC的底边,AD⊥BC,∠BAC≠90°,将此三角形纸片沿AD剪开,得到两个三角形,若把这两个三角形拼成一个平行四边形,则能拼出中心对称图形 个。
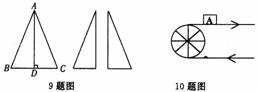
10.如图,半径为
二、选择题(选择题(每小题3分,共18分)
11.下列计算正确的是 ( )
A.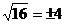 B.
B.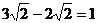
C.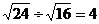 D.
D.
12.如图,将半径为

A.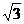 cm C.
cm C.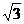 cm D.
cm D.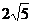 cm
cm
13.等腰△ABC的腰AB=AC=4cm,若以A的圆心,2cm为半径的圆与BC相切,∠BAC的度数为 ( )
A.30° B.60° C.90° D.120°
14.如图,△PQR是⊙O的内接正三角形,四边形ABCD是⊙O的内接正方形,BC//QR,则∠AOQ= ( )
A.60° B.65° C.72° D.75°
15.一块等边三角形的木板,边长为1,现将木板沿水平线翻滚(如图),那么B点从开始至结束所走过的路径长度为 ( )
A.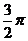 B.
B.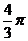 C.4 D.2+
C.4 D.2+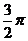

16.某经济开发区今年一月份工业产值达50亿元,第一季度总产值为175亿元,问2、3月份平均每月的增长率是多少?设平均每月的增长率为x,根据题意得方程为 ( )
A.50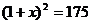 B.50+50
B.50+50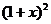 =175
=175
C.50(1+x)+50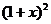 =175 D.50+50(1+x)+50
=175 D.50+50(1+x)+50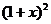 =175
=175
三、解答题(每小题5分,共20分)
17.计算: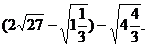
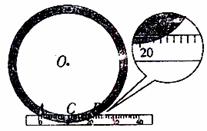
18.如图,某建筑工地上一钢管的横截面是圆环形。王师傅将直尺边缘紧靠内圆,直尺与外圆交于点A,B(AB与内圆相切于点C,其中点A在直尺的零刻度处)。请观察图形,写出线段AB的长(精确到1cm),并根据得到的数据计算该钢管的横截面积。(结果用含π的式表示)
19.解方程x2=4x+2时,有一位同学解答如下:
解:∵a=1,b=4,c=2,b2-4ac=42-4×1×2=8,
∴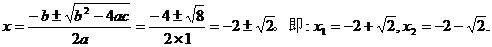
请你分析以上解答有无错误,如有错误,请指出错误的地方,并写出正确的解题过程。
 20.如图,O是圆柱木块底面的圆心,过底面的一条弦AD,沿母线AB剖开,得剖面矩形ABCD,AD=24cm,若弧AmD的长为底面周长的
20.如图,O是圆柱木块底面的圆心,过底面的一条弦AD,沿母线AB剖开,得剖面矩形ABCD,AD=24cm,若弧AmD的长为底面周长的 ,如图所示。求⊙O的半径。
,如图所示。求⊙O的半径。

四、解答题(每小题6分,共18分)
21.一个农户用24米长的篱笆围成一排一面靠墙、大小相等且彼此相连的三个矩形鸡舍,如图所示,要使三个鸡舍的总面积为36m2,那么每个鸡舍的长、宽各应是多少?

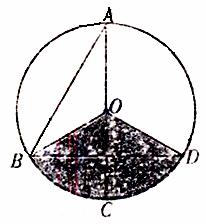
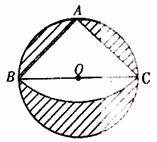
22.如图,已知在⊙O中,AB= ,AC是⊙O的直径,AC⊥BD于F。∠A=30°,求图中阴影部分的面积。
,AC是⊙O的直径,AC⊥BD于F。∠A=30°,求图中阴影部分的面积。
23.一名跳水运动员进行10m跳台训练,在正常情况下,运动员必须在距水面5m以前完成规定的翻腾动作,并且调整好入水姿势,否则就容易出现失误。假设运动员起跳后的运动时间t(s)和运动员距离水面的高度h(m)满足关系:h=10+2.5t-5t2,那么他最多有多长时间完成规定动作?
五、解答题(每小题8分,共24分)
24.认真观察图中的4个图的阴影部分构成的图案,回答下列问题:

(1)请写出这四个图案都具有的两个共同特征。
特征1:
特征2:
(2)请在图②中设计出你心中最美丽的图案,使它也具备你所写出的上述特征。

25.如图所示,有一直径是1m的圆形铁皮,要从中剪出一个圆心角为90°的扇形ABC。
(1)求被剪掉的阴影部分的面积;
(2)用所剪的扇形铁皮围成一个圆锥,该圆锥的底面半径是多少?(结果可用根号表示)
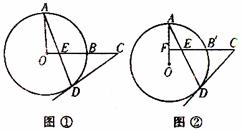
26.(1)如图①,OA、OB是⊙O的两条半径,且OA⊥OB,点C是OB延长线上任意一点,过点C作CD切⊙O于点D,连结AD交OC于点E。求证CD=CE。
(2)若将图①中的半径OB所在直线向上平行移动交OA于F,交⊙O于B′,其他条件不变(如图②),那么上述结论CD=CE还成立吗?为什么?
六、解答题(每小题10分,共20分)
27.某商场将某种商品的售价从原来的每件40元经两次调价后调至每件32.4元。
(1)若该商店两次调价的降价率相同,求这个降价率;
(2)经调查,该商品每降价0.2元,即可多销售10件。若该商品原来每月可销售500件,那么两次调价后,每月可销售该商品多少件?
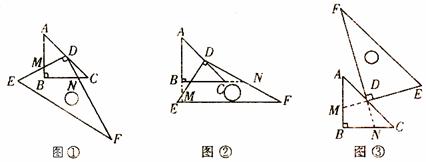
28.如图,已知△ABC中,AB=BC=1,∠ABC=90°,把一块含30°角的直角三角板DEF
的直角顶点D放在AC的中点上(直角三角板的短直角边为DE,长直角边为DF),将直角三角板绕点D按逆时针方向旋转。
(1)在图①中,DE交AB于M,DF交BC于N。
①证明:DM=DN;
②在这一旋转过程中,直角三角板DEF与△ABC的重叠部分为四边形DMBN,请说明四边形DMBN的面积是否发生变化?若发生变化,请说明是如何变化的?若不发生变化,求出其面积;
(2)继续旋转至如图②的位置,延长AB交DE于M,延长BC交DF于N,DM=DN是否仍然成立?若成立,请给出证明,若不成立,请说明理由;
(3)继续旋转至如图③的位置,延长FD交BC于N,延长ED交AB于M,DM=DN是否仍然成立?请写出结论,不用证明。