2007-2008学年第一学期期中考试八年级
数学试卷
时间:90分钟 满分:100分
一、选择题(每题3分,共30分)
1.已知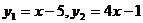 ,使不等式
,使不等式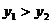 成立的
成立的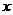 值中最大整数是( ).
值中最大整数是( ).
A.2 B.
2.如图所示,已知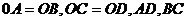 相交于
相交于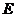 ,则图中全等的三角形的个数是( ).
,则图中全等的三角形的个数是( ).
A.2 B.
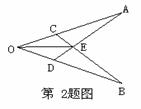
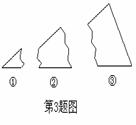
3.如图所示,某同学将一块三角形的玻璃打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的办法是( ).
A.带①去 B.带②去 C.带③去 D.带①②去
4.已知点(-2,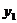 ),(-1,
),(-1, ),(1,
),(1,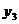 )都在直线
)都在直线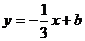 上,则
上,则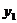 ,
, ,
,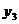 的值的大小关系是( ).
的值的大小关系是( ).
A.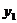
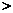

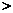
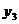 B.
B.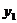
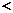

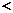
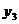 C.
C.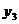
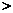
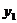
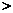
 D.
D.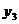 <
<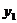 <
<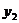
5.函数 的图像与函数
的图像与函数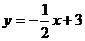 的图像平行,且与
的图像平行,且与 轴的交点为
轴的交点为 (0,2),则其函数表达式为( ).
(0,2),则其函数表达式为( ).
A.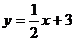 B.
B.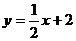 C.
C.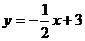 D.
D.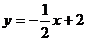
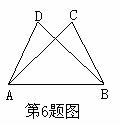
6.如图, ≌
≌ ,
, 和
和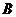 ,
,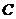 和
和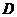 是对应顶点,如果
是对应顶点,如果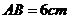 ,
,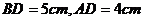 ,那么
,那么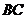 的长是( ).
的长是( ).
A.
7.已知一次函数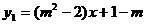 与
与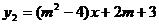 的图像与
的图像与 轴交点的纵坐标互为相反数,则
轴交点的纵坐标互为相反数,则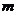 的值为( ).
的值为( ).
A.-2 B.
8.若直线 与
与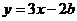 相交于
相交于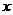 轴上,则
轴上,则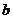 的值是( ).
的值是( ).
A.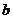 =-3
B.
=-3
B.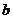 =-
=-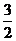 C.
C.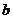 =-
=-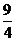 D.
D.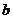 =6
=6
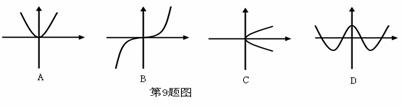
9.下列各曲线中不能表示y是x的函数的是 ( )
10.一个容量为80的样本最大值是146,最小值是50,取组距为10,则可以分成 ( )
A.8组 B.9组 C.10组 D.11组
二、填空题(每题3分,共15分)
11.已知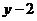 与
与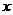 成正比例,当
成正比例,当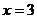 时,
时,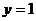 ,那么
,那么 与
与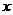 之间的函数关系式为______.
之间的函数关系式为______.
12.一个扇形统计图中,某部分所对应的扇形圆心角为36°,则该部分所占总体的百分比是______.
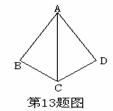
13.如图所示, ,要证明
,要证明 与
与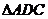 全等,还需要补充的条件是________.
全等,还需要补充的条件是________.
14.若一次函数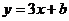 经过点
经过点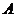 (1,7),则
(1,7),则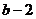 =_______,该函数图像经过点
=_______,该函数图像经过点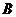 (4,______)和点
(4,______)和点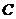 (_____,0).
(_____,0).
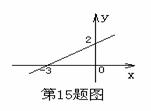
15.函数 的图像如图6所示,则当
的图像如图6所示,则当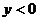 时,
时,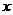 的取值范围是________.
的取值范围是________.
三、解答题(16题6分,17题7分,18、19、20每题8分,21、22每题9分,共55分)
16.如图是某汽车行驶的路程S(km)与时间t(min)的函数关系图。观察图中所提供的信息,解答下列问题:

(1)汽车在前9分钟内的平均速度是多少?
(2)汽车在中途停了多久?
(3)当16≤t≤30时,求S与t的函数关系式.
17.如图,已知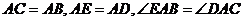 ,问
,问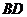 与
与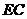 相等吗? 并说明理由。
相等吗? 并说明理由。
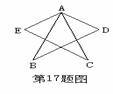
18.如图所示, ,
, 在
在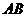 上,试说明:(1)点
上,试说明:(1)点
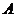 在
在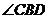 的平分线上.(2)
的平分线上.(2) .
.

19.如图所示,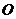 为码头,
为码头,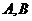 两个灯塔与码头的距离相等,
两个灯塔与码头的距离相等, 为海岸线,一轮船离开码头,计划沿
为海岸线,一轮船离开码头,计划沿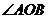 的平分线航行,在航行途中,测得轮船与灯塔
的平分线航行,在航行途中,测得轮船与灯塔 和灯塔
和灯塔 的距离相等,试问轮船航行时是否偏离预定航线,请说明理由.
的距离相等,试问轮船航行时是否偏离预定航线,请说明理由.
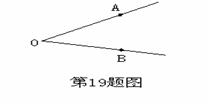
20.某车间有20名工人,每人每天加工甲种零件5个或乙种零件4个,在这20名工人中,派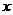 人加工甲种零件,其余人加工乙种零件,已知每加工一个甲种零件可获利16元,每加一个乙种零件可获利24元.
人加工甲种零件,其余人加工乙种零件,已知每加工一个甲种零件可获利16元,每加一个乙种零件可获利24元.
(1)写出此车间每天所获利润 (元)与
(元)与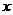 (人)之间的函数关系式.
(人)之间的函数关系式.
(2)若要使车间每天获利不低于1800元,问至少应派多少人加工乙种零件.
21.下面两个统计图(如图所示)反映的是某市甲、乙两所中学的学生参加课外活动的情况,请你通过图中信息回答下列问题:
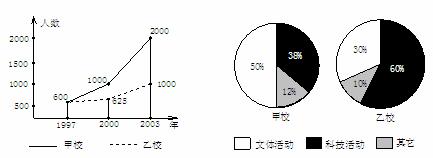
(1)通过对图(1)的分析,写出一条你认为正确的结论.
(2)通过对图(2)的分析,写出一条你认为正确的结论.
(3)2003年甲、乙两所中学参加科技活动的学生人数共有多少?
22.某中学对初二年级女生仰卧起坐的测试成绩进行统计分析,将数据整理后,画出如下频数分布直方图,如图,已知图中从左到右的第一、第二、第三、第四、第六小组的频率依次是0.10,0.15,0.20,0.30,0.05,第五小组的频数是36,根据所给的图填空:
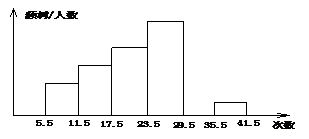
第22题图
(1)第五小组的频率是_______,请补全这个频数分布图.
(2)参加这次测试的女生人数是______;若次数在24(含24次)以上为达标(此标准为中考体育标准),则该校初二年级女生的达标率为________.
(3)请你用统计知识,以中考体育标准对该区12所中学初二学生仰卧起坐成绩的达标率作一个估计.