2007年滨州市博兴中考模拟试题(一)
数学试题
一、选择题:(本题有10小题,共30分。每小题只有一个选项是正确的,不选、多选、错选均不给分)
1.冬季的一天室内温度是
A.
2.如图是由一些相同的小正方体构成的几何体的三视图,则这些相同的小正方体的个数是 主视图 左视图 俯视图

A.4 B.
3.化简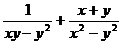 的结果是
的结果是
A. B.
B. C.
C.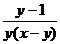 D.
D.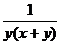
4.如果从一卷粗细均匀的电线上截取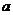 克,再称得剩余电线的质量为
克,再称得剩余电线的质量为 克,那么原来这卷电线的总长度是
克,那么原来这卷电线的总长度是
A. B.
B.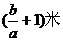 C.
C. D.
D.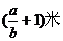
5.如图,⊙O是ABC的外接圆,连接OA、OC,⊙O的半径R=2, ,则AC的长为
,则AC的长为
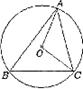
A.3 B.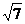 C.
C.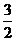 D.
D.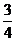
6.小颖的家与学校的距离为 千米,她从家到学校先以匀速
千米,她从家到学校先以匀速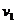 跑步前进,后以匀速
跑步前进,后以匀速 (
( <
<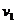 )走完余下的路程,共用了
)走完余下的路程,共用了 小时,下列能大致表示小颖离家的距离
小时,下列能大致表示小颖离家的距离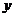 (千米)与离家时间
(千米)与离家时间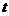 (小时)之间关系的图像是
(小时)之间关系的图像是
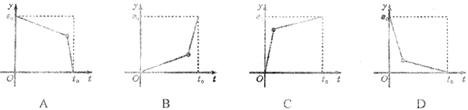
7.如图,农村常搭建横截面为半圆形的全封闭塑料薄膜蔬菜大棚。如果不考虑塑料薄膜埋在土里的部分,那么搭建一个这样的蔬菜大棚需用塑料薄膜的面积是

A.64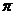 m2 B.
m2 B.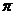 m2 C.78
m2 C.78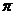 m2 D.80
m2 D.80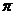 m2
m2
8.已知抛物 ,下列说法中正确的是
,下列说法中正确的是
A.当 =1时,函数取得最小值
=1时,函数取得最小值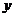 =3
=3
B.当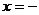 1时,函数取得最小值
1时,函数取得最小值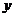 =3
=3
C.当 =1时,函数取得最小值
=1时,函数取得最小值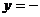 3
3
D.当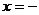 1时,函数取得最小值
1时,函数取得最小值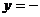 3
3
9.为了美化校园,同学们要在一块正方形空地上种上草,他们设计了如图所示的图案,其中阴影部分为绿化面积,哪个图案的绿化面积与其他图案的绿化面积不相等

10.如图,在□ABCD中,EF//AB,GH//AD,EF与GH交于点O,则该图中的平行四边形的个数共有

A.7 B.8 C.9 D.11
二、填空题(本大题共8小题,每小题4分,共32分)
11.如果关于 的不等式
的不等式 和
和 的解集相同,则
的解集相同,则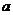 的值为
;
的值为
;
12.用计算器比较大小:
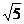 (填“>”、“=”、“<”)。
(填“>”、“=”、“<”)。
13.杏花村现有手机188部,比2004年底的3倍还多17部,则该村2004年底有手机 部。
14.若矩形的面积为6,则矩形的长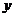 关于宽
关于宽 (
( >0)的函数关系式为
。
>0)的函数关系式为
。
15.小明的身高是1.7 m,他的影长是2m,同一时刻学校旗杆的影长是10m,则旗杆的高是____ m。
16.如图,正方形ABCD的边长为8,M在DC上,且DM=2,N是AC上一动点,则DN+MN的最小值为 。

17.在解分式方程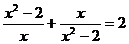 时,若设了
时,若设了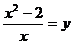 ,则原分式方程可化为 。
,则原分式方程可化为 。
18.如图,作△ABC的中线AD,并将△ADC绕点D旋转l80º,那么点C与点B重合,点A转到A´点,不难发现AC= A′B,AD= A′D,BD=DC。如果知道AB=4cm,AC=3cm,则中线AD的范围 。

三、解答题(本题有7个小题,共58分)
19.(5分)甲乙两人各持标有1、2、3的三张扑克,每次每人出一张,若出现的数字之和为3,则甲加一分,否则不得分;若出现的数字之和为7,则乙加一分,否则不得分;甲、乙各出牌10次,得分高者胜。
(1)请用列表法求出甲获胜的概率;
(2)这个游戏公平吗?请说明理由。
20.(7分)等腰梯形ABCD中,AD//BC,∠DBC=45º,翻折梯形ABCD,使点B重合于点D,折痕分别交边AB、BC于点F、E。若AD=2,BC=8。
求(1)BE的长:(2)∠CDE的正切值。

21.(8分)如图, 、
、 分别表示一种白炽灯和一种节能灯的费用
分别表示一种白炽灯和一种节能灯的费用 (费用=灯的售价+电费,单位:元)与照明时间
(费用=灯的售价+电费,单位:元)与照明时间 (小时)的函数图像,假设两种灯的使用寿命都是2000小时,照明效果一样。若
(小时)的函数图像,假设两种灯的使用寿命都是2000小时,照明效果一样。若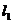 过两点(0,2)和(500,17),
过两点(0,2)和(500,17), 过两点(0,20)和(500,26)。
过两点(0,20)和(500,26)。
(1)根据图像分别求出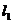 、
、 的函数关系式;
的函数关系式;
(2)当照明时间为多少时,两种灯的费用相等?
(3)小亮房间计划照明2500小时,他买了一个白炽灯和一个节能灯,请你帮他设计最省钱的用灯方法。(直接给出答案,不必写出解答过程)。

22.(8分)某研究性学习小组,为了了解本校初一学生一天中做家庭作业所用的大致时间(时间以整数记,单位:分钟),对本校的初一学生做了抽样调查,并把调查得到的所有数据(时间)进行整理,分成五个时间段,绘制成统计图(如图所示),请结合统计图中提供的信息,回答下列问题:
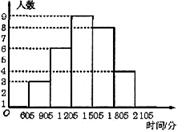
(1)这个研究性学习小组所抽取样本容量是多少?
(2)在被调查的学生中,一天做家庭作业所用的大致时间超过120分钟(不包括120分钟) 的人数占被调查学生总人数的百分之几?
(3)这次调查得到的所有数据的中位数落在了五个时间段中的哪一段内?
23.(8分)已知某山区的平均气温与该山区的海拔高度的关系见下表:
海拔高度(单位:米)
0
100
200
300
400
500
平均气温(单位:℃)
22
21.5
21
20.5
20
19.5
(1)若海拔高度用 (米)表示,平均气温用
(米)表示,平均气温用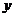 (℃)表示,试写出
(℃)表示,试写出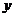 与
与 之间的函数关系式;
之间的函数关系式;
(2)若某种植物适宜生长在18℃~20℃(包括l8℃,也包括20℃)的山区,请问该植物适宜种植在海拔为多少米的山区?
24.(10分)在△CDE中,∠C=90º,CD,CE的长分别为 ,
, ,且DE
,且DE 。
。
(1)求证: ;
;
(2)若 =2,抛物线
=2,抛物线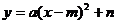 与直线
与直线 交于
交于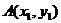 和
和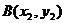 两点,求
两点,求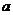 的取值范围。
的取值范围。
25.(12分)已知:如图,AB是⊙O的直径,点P是AB延长线上一点,PC切⊙O于点C,在射线PA上截取PD=PC,连接CD,并延长交⊙O于点E。

(1)求证:∠ABC+∠BCF=90º;∠BCF=∠E。
(2)求证:∠ABE=∠BCE。
(3)当点P在AB的延长线上运动时,判断sin∠BCE的值是否随点P位置的变化而变化,提出你的猜想并加以证明。