2006-2007学年度潍坊市诸城九年级下学期
单元过关考试(四)
第I卷(选择题 共36分)
一、选择题(本题共12小题,共36分。在每小题给出的四个选项中,只有一个是正确的,请把正确选项的字母填在题后的括号内。每小题选对得3分,选错、不选或选出的答案超过一个,均记零分。)
1.一个不透明的袋中装有除颜色外其余均相同的5个红球和3个黄球,从中随机摸出一 个,则摸到黄球的概率是
A. B.
B.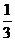 C.
C. D.
D.
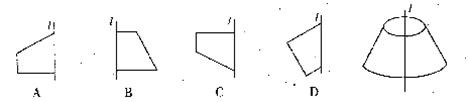
2.将下面的直角梯形绕直线l旋转一周,可以得到右边立体图形的是
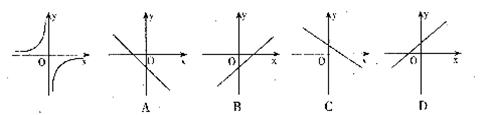
3.函数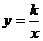 (k≠0)的图象如图所示,那么函数y=kx-k的图象大致是
(k≠0)的图象如图所示,那么函数y=kx-k的图象大致是
4.如果从一卷粗细均匀的电线上截取
A. 米 B.(
米 B.(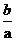 +1)米 C.(
+1)米 C.(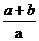 +1)米 D.(
+1)米 D.(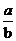 +1)米
+1)米
5.如图,有两个形状相同的星星图案,则x的值为
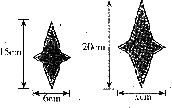
A.15 B.
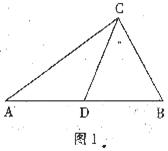
6.如图:已知AD为等腰△ABC底边上的高,且tan∠B,AC上有一点E,满足AE:EC=2:3,那么tan∠ADE是

A. B.
B.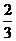
C.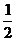 D.
D.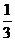
7.下面是两户居民家庭全年各项支出的统计图。根据统计图,下列对两户教育支出占全年总支出的百分比作出的判断中正确的是

A.甲户比乙户大 B.乙户比甲户大
C.甲、乙两户一样大 D.无法确定哪一户大
8.已知方程组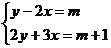 的解x、y满足2x+y≥0,则m的取值范围是
的解x、y满足2x+y≥0,则m的取值范围是
A.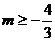 B.
B.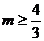 C.
C. D.
D.
9.已知在正方形网格中,每个小方格都是边长为1的正方形,A、B两点在小方格的顶点上,位置如图所示,点C也在小方格的顶点上,且以A、B、C为顶点的三角形面积为1,则点C的个数为
A.3个 B.4个 C.5个 D.6个

10.如图,正方形ABCD的边长为2,点E在AB边上,四边形EFGB也为正方形,设△AFC的面积为S,则
A.S=2 B.S=2.
11.二次函数 的图象如图所示,则点A(a,b)所在象限为
的图象如图所示,则点A(a,b)所在象限为

A.第一象限 B.第二象限
C.第三象限 D.第四象限
12.数字解密:第一个数是3=2+1,第二个数是5=3+2,第三个数是9=5+4,第四个数是17=9+8 ……观察并猜想第六个数是
A.35 B.
第II卷(非选择题共84分)
二、填空题(本题共5小题,共15分.只要求填写最后结果,每小题填对得3分,其中,第16、17两小题为选做题,只须做A、B题中的一个即可,若两题都做,只以A题计分。)
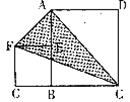
13.如图,P是正三角形ABC内的一点,且PA=6,PB=8, PC=10。若将△PAC绕点A逆时针旋转后,得到△P′AB,则∠APB= 。

14.分解因式: =
=
15.圆柱的底面半径是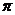 )
)
16.(A题)如图,一圆与平面直角坐标系中的X轴切于点A(8,O),与y轴交于点B(0,4),C(0,16),则该圆的直径为 。
(B题)将多项式 加上一个整式,使它成为完全平方式,试写出满足上述条件的三个整式:
, , 。
加上一个整式,使它成为完全平方式,试写出满足上述条件的三个整式:
, , 。
17.(A题)如图1,三角形纸片∠ABC中,∠A=65°,∠B=75°,将纸片的一角折叠,使点C落在△ABC内,若∠1=20°,则∠2的度数为 。
(B题)如图2,D、E为AB、AC的中点,将△ABC沿线段DE折叠,使点A落在点F处,若∠B=50°,则∠BDF= 。

三、解答题(本题共7小题,共69分。解答应写出文字说明、证明过程或推演步骤。)
18.(本小题满分8分)
某中学图书馆将图书分为自然科学、文学艺术、社会百科、数学四类。在“爱校读书月”活动期间,为了解图书的借阅情况,图书管理员对本月各类图书的借阅量进行了统计,图1和图2是图书管理员通过采集数据后,绘制的两幅不完整的频率分布表与频数分布直方图。请你根据图表中提供的信息,解答以下问题:
图书种类
频数
频率
自然科学
400
0.20
文学艺术
1000
0.50
社会百科
500
0.25
数 学
(1)(2分)填充图1频率分布表中的空格。

(2)(2分)在图2中,将表示“自然科学”的部分补充完整.
(3)(2分)若该学校打算采购一万册图书,请你估算“数学”类图书应采购多少册较合适?
(4)(2分)根据图表提供的信息,请你提出一条合理化的建议。
19.(本小题满分8分)如图甲,李叔叔想要检测雕塑底座正面四边形ABCD是否为矩形,但他随身只带了有刻度的卷尺,请你设计一种方案,帮助李叔叔检测四边形ABCD是否为矩形(图乙供设计备用)。


20.(本小题满分9分)
日照市是中国北方最大的虾养殖产区,被国家农业部列为对虾养殖重点区域;贝类产品西施舌是日照特产,沿海某养殖场计划今年养殖无公害标准化对虾和西施舌,由于受养殖水面的制约,这两个品种的苗种的总投放量只有50吨。根据经验测算,这两个品种的种苗每投放一吨的先期投资、养殖期间的投资以及产值如下表:(单位:千元/吨)
品种
先期投资
养殖期间投资
产值
西施舌
9
3
30
对虾
4
10
20
养殖场受经济条件的影响,先期投资不超过360千元,养殖期间的投资不超过290千元。设西施舌种苗的投放量为x吨.
(1)求x的取值范围;
(2)设这两个品种产出后的总产值为y(千元),试写出y与x之间的函数关系式,并求出当x等于多少时,y有最大值?最大值是多少?
21.(本小题满分10分)
已知反比例函数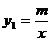 (m≠0)的图象经过点A(一2,1),一次函数
(m≠0)的图象经过点A(一2,1),一次函数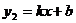 (k≠0)的图象经过点C(0,3)与点A,且与反比例函数的图象相交于另一点B。
(k≠0)的图象经过点C(0,3)与点A,且与反比例函数的图象相交于另一点B。
(1)分别求出反比例函数与一次函数的解析式;(6分)
(2)求点B的坐标.(4分)
22.(本小题满分11分)
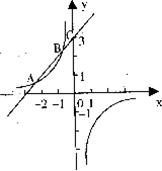
如图,从⊙0外一点A作⊙O的切线AB、AC,切点分别为B、C,且⊙0直径BD=6,连结 CD、A0。
(1)求证:CD∥A0;(3分)
(2)设CD=x,AO=y,求y与x之间的函数关系式,并写出自变量x的取值范围;(4分)
(3)若AO + CD=11,求AB的长.(4分)
23.(本小题满分11分)
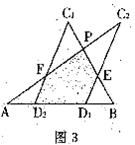
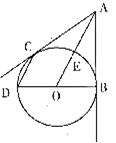
已知∠AOB=90°,在∠AOB的平分线OM上有一点C,将一个三角板的直角顶点与C重合,它的两条直角边分别与
当三角板绕点C旋转到CD与OA垂直时(如图1);易证:0D+OE= OC。当三角板绕点C旋转到CD与OA不垂直时,在图2、图3这两种情况下,上述结论是否还成立?若成立,请给予证明:若不成立,线段OD、OE、OC之间又有怎样的数量关系?请写出你的猜想,不需证明。
OC。当三角板绕点C旋转到CD与OA不垂直时,在图2、图3这两种情况下,上述结论是否还成立?若成立,请给予证明:若不成立,线段OD、OE、OC之间又有怎样的数量关系?请写出你的猜想,不需证明。
24.(本小题满分12分)
如图1所示,一张三角形纸片ABC,∠ACB=90°,AC=8,BC=6。沿斜边AB的中线CD把这张纸片剪成△AC1D1和△BC2D2两个三角形(如图2所示)将纸片△AC1D1沿直线D2B(AB)方向平移(点A,D1D2,B始终在同一直线上),当点D1与点B重合时,停止平移。在平移的过程中,C1D1与BC2交于点E,AC1与C2D2、BC2分别交于点F、P。
(1)当△AC1D1平移到如图3所示位置时,猜想D1E与D
(2)设平移距离D2D1为x,△AC1D1和△BC2D2重复部分面积为y,请写出y与x的函数关系式,以及自变量的取值范围;
(3)对于(2)中的结论是否存在这样的x,使得重复部分面积等于原△ABC纸片面积的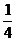 ?若存在,请求出x的值;若不存在,请说明理由。
?若存在,请求出x的值;若不存在,请说明理由。