2007年甘肃省兰州市初中毕业生学业考试试卷
数学(A)
(全卷共计150分,考试时间120分钟)
一.选择题(本题共12个小题,每小题4分,共计48分。在每小题给出的4个选项中,只有一项是符合题目要求的.)
1.下列方程中是一元二次方程的是( ).
A、2x+1=0
B、y2+x=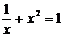
2.把Rt△ABC各边的长度都扩大3倍得Rt△A'B'C',那么锐角A、A'的余弦值的关系为( ).
A、cosA=cosA' B、cosA=3cosA' C、3cosA=cosA' D、不能确定
3.下列函数中,自变量x的取值范围是x>2的函数是( ).
A、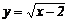 B、
B、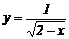 C、
C、 D、
D、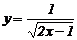
4.下列说法正确的是( ).
A、在同一年出生的367名学生中,至少有两人的生日是同一天
B、彩票中奖的机会是1%,买100张一定会中奖
C、天气预报说每天下雨的概率是50%,所以明天将有一半的时间在下雨
D、抛一枚图钉钉尖着地和钉尖朝上的概率一样大
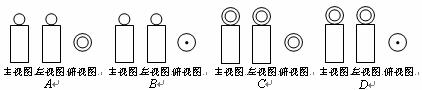
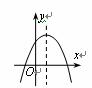
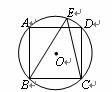
5.下列四个图形中,既是轴对称图形,又是中心对称图形的是( ).
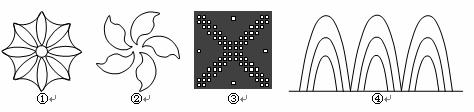
|

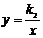 的图象大致是( ).
的图象大致是( ).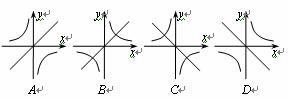
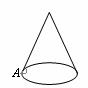
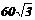 cm
B、
cm
B、 cm
C、
cm
C、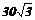 cm
D、
cm
D、
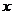 的增大而减小。请你写一个满足上述性质的函数解析式_________________.
的增大而减小。请你写一个满足上述性质的函数解析式_________________.




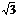 -1)0+tan60°
-1)0+tan60°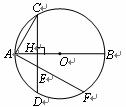


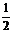 <x<4时,(3)小题中平行四边形的面积是否有最大值,若有,请求出,若无,请说明理由.
<x<4时,(3)小题中平行四边形的面积是否有最大值,若有,请求出,若无,请说明理由.