2007年济南市天桥区九年级毕业升学模拟考试
数学模拟试题(B)
本试卷分第I卷(选择题)和第II卷(非选择题)两部分.第I卷1~2页,第II卷3~8页.共120分.考试时间l20分钟.
第I卷(选择题共48分)
注意事项:
1.数学考试允许使用不含有存储功能的计算器.
2.答第I卷前,考生务必将自己的姓名、准考证号、考试科目用铅笔涂写在答题卡上。
3.选择题为四选一题目,每小题选出答案后,用铅笔把答题卡上对应题目的答案标号 涂黑.如需改动,用橡皮擦干净后,再选涂其他答案,不能答在试卷上.
4.考试结束,监考教师将本试卷和答题卡一并收回.
一、选择题:(本大题共l2小题,每小题4分,共48分。在每小题给出的四个选项中,只有一项符合题目要求)
1.一个数的相反数是3,则这个数是
A.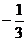 B.
B.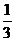 C.一3 D.3
C.一3 D.3
2.在 中,
中,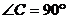 ,若
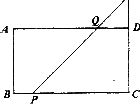
,若 ,则sinA的值为
,则sinA的值为
A. B.
B.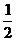 C.
C.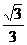 D.
D.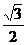
3.下列运算中,正确的是
A.
B.
C.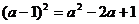
D.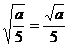
4.三角形两边长分别为3和6,第三边是方程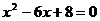 的解,则此三角形周长是
的解,则此三角形周长是
A.1l B.13 C.11或l3 D.不能确定
5.样本6,7,8,9,10,10,10的中位数和众数分别是
A.9,3 B.8,10 C.10,l0 D.9,10
6.下列命题中,真命题是
A.两条对角线相等的四边形是矩形
B.两条对角线垂直的四边形是菱形
C.两条对角线垂直且相等的四边形是正方形
D.两条对角线相等的平行四边形是矩尹
7.如图①是一个正三棱柱毛坯,将其截去一部分,得到一个工件如图②对于这个工件,俯视图、主视图依次是
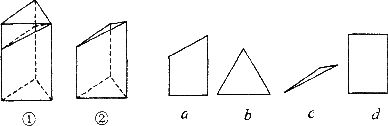
A.c、a B.c、d C.b、d D.b、a
8.反比例函数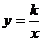 与直线
与直线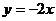 相交于点A,A点的横坐标为一l,则反比例函数的解析式为
相交于点A,A点的横坐标为一l,则反比例函数的解析式为
A. B.
B. C.
C. D.
D.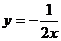
9.如图,用8块相同的长方形地砖拼成一个矩形地面,则每块长方形地砖的长和宽分别是
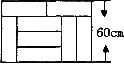
A.48cm,12cm B.48cm,16cm
C.44cm,l6cm D.45cm,15cm
10.如图,已知直线MN切⊙A于4点,AC为的⊙O弦,CO的延长线交MN于N,若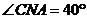 ,则
,则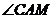 等于
等于

A.50° B.65° C.80° D.85°
11.如图,等边△ABC外一点P,P点落在∠ABC内,设P到AB、AC、BC的距离分别为hl、h2、h3,且满足h1-h2+h3=6,则
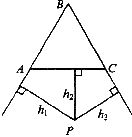
A.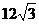 B.
B.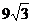 C.
C.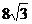 D.
D.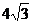
12.如图,边长为2的正方形ABCD中,顶点A的坐标是(0,2),一次函数 的图象从过原点的位置沿y轴向上平移,当直线
的图象从过原点的位置沿y轴向上平移,当直线 扫过正方形的面积为3时,t的值为
扫过正方形的面积为3时,t的值为

A.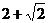 B.3 C.
B.3 C.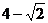 D.2
D.2
第II卷(非选择题,共72分)
注意事项:
1.第II卷共6页,用蓝、黑钢笔或圆珠笔直接答在试卷上.
2.答卷前将密封线内的项目填写清楚.
二、填空题:(本大题共5小题,每小题3分,共15分,把答案填写在题中横线上)
13.分解因式: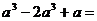 ___________
___________
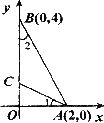
14.如图,已知两点A(2,0), B(0,4),且 ,则点C的坐标是__________
,则点C的坐标是__________
15.如图,一只蚂蚁在图案内任意爬动,若两圆的半径分别为lcm和2cm,则蚂蚁停在阴影内的概率为_____________

16.如图,在矩形ABCD中,AB=4,BC=7,P是BC边上与B点不重合的动点,过点P的直线交CD延长线于R,交AD于Q(Q与D不重合),且 ,设BP=x,梯形ABPQ的面积为y,则y与
,设BP=x,梯形ABPQ的面积为y,则y与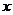 的函数关系式为____________.
的函数关系式为____________.
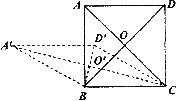
17.边长为2的正方形ABCD的两条对角线交于点0,把BA与CD同时分别绕点B和C逆时针方向旋转,此时正方形 ABCD随之变成四边形A’BCD',设A’C、BD’交于点O’则旋转60°时,由点O运动到点O’所经过的路径的长是______________.
三、解答题:(本大题共7小题,共57分,解答应写出文字说明,证明过程或演算步骤)
18.(本小题满分7分)
(1)化简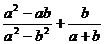
(2)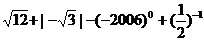
19.(本小题满分7分)完成下列各题:
(1)如图,平行四边形ABCD中,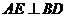 于E,
于E, 于F,
于F,
证明: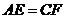

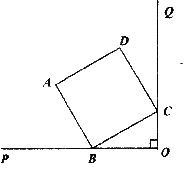
(2)已知,如图 ,边长为2cm的正方形ABCD的顶点B在OP上,C在OQ上且
,边长为2cm的正方形ABCD的顶点B在OP上,C在OQ上且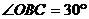 ,求出点A到OP的距离.
,求出点A到OP的距离.
20.(本小题满分8分)
(1)解不等式组 并把解集在数轴上表示出来.
并把解集在数轴上表示出来.
(2)已知方程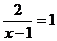 的解是a,求关于x的方程
的解是a,求关于x的方程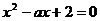 的解.
的解.
21.(本小题满分8分)有四张背面相同的纸牌A,B,C,D,其正面分别画有四个不同的几何图形(如图).小华将这4张纸牌背面朝上洗匀后摸出一张,放回洗匀后再摸出一张.
(1)用树状图(或列表法)表示两次摸牌所有可能出现的结果(纸牌可用A,B,C,D表示):
(2)求摸出两张牌面图形都是中心对称图 形的纸牌的概率.

22.(本小题满分9分)某公司为了扩大经营,决定购进6台机器用于生产某种活塞.现有甲、乙两种机器供选择,其中每种机器的价格和每台机器日生产活塞的数量如下表所示.经过预算,本次购买机器所耗资金不能超过34万元.
(1)按该公司要求可以有几种购买方案?
(2)若该公司购进的6台机器的日生产能力不低于380个,那么为了节约资金应选择哪种购买方案?
甲
乙
价格(万元/台)
7
5
每台日产量(个)
100
60
23.(本小题满分9分)如图,点P在x正半轴上,以P为圆心的⊙P与x轴交于A、B两点,与y轴交于C、D两点,⊙P的半径是4,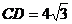 .
.
(1)求点P和点C的坐标;
(2)过点C作⊙P的切线,交x轴于E,求点E的坐标;
(3) 若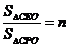 ,求满足下列两个条件的抛物线解析式:
,求满足下列两个条件的抛物线解析式:
①过点P、E:
②抛物线的顶点到x轴的距离为n
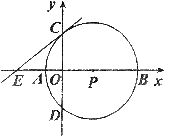
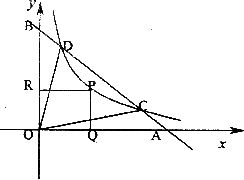
24。(本小题满分9分)如图,直线AB过点A(m,0),B(0,n)(m>0,n>0)反比例函数的图象与AB交于C,D两点,P为双曲线 一点,过P作
一点,过P作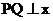 轴于Q,
轴于Q,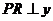 轴于R,请分别按(1)(2)(3)各自的要求解答闷题。
轴于R,请分别按(1)(2)(3)各自的要求解答闷题。
(1)若m+n=10,当n为何值时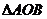 的面积最大?最大是多少?
的面积最大?最大是多少?
(2)若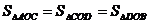 ,求n的值:
,求n的值:
(3)在(2)的条件下,过O、D、C三点作抛物线,当抛物线的对称轴为x=1时,矩形PROQ的面积是多少?