2007年聊城市高唐县中考模拟考试二
数学试卷
注意事项:
1.本试卷分为试题和答卷两部分。
2.试题由第Ⅰ卷和第Ⅱ卷组成,共6页,第Ⅰ卷为选择题,48分;第Ⅱ卷为非选择题,102分,共150分。考试时间为120分钟。
3.答第Ⅰ卷前,务必将自己的姓名、准考证号、考试科目涂写在答题卡上,每题选出答案后,都必须用2B铅笔把答题卡上对应题目的答案标号(ABCD)涂黑,如需改动,必须先用橡皮擦干净,再改涂其它答案。
4.第Ⅱ卷试题的答案直接写在答卷上,考试结束,将答题卡、答卷和试题一并收回。 第Ⅰ卷(选择题,共48分)
一、选择题(本题共12个小题,每小题4分,在每小题给出的四个选项中,只有一项符合题目要求)
1.一元二次方程菇x 一2x=0的解是( )
一2x=0的解是( )
A.0 B.2 C.0,一2 D.0,2
2.某工厂计划产值为a元,比去年增长10%,如果今年实际产值可超过计划1%,那么实际产值将比去年增长( )
A.11% B.10.1% C.11.1% D.10.01%
3.如图,在平行四边形ABCD中,AE⊥BC,垂足为E,AF⊥CD,垂足为F,若AE:AF=2 :3,平行四边形ABCD的周长为40,则AB的长为( )
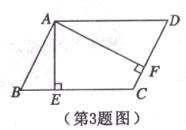
A.12 B.9 C.8 D.6
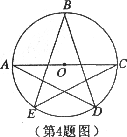
4.如图,已知A、B、C、D、E均在⊙O上,且AC为⊙O的直径,则∠A+∠B+∠C= ( )
A.180° B.90° C.45° D.30°
5.已知点A(一2,y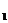 ),B(1,y
),B(1,y ),C(3,y
),C(3,y )都在函数y= 一
)都在函数y= 一 的图象上,那么比较y
的图象上,那么比较y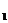 ,y
,y ,y
,y 大小正确的是( )
大小正确的是( )
A.y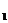 > y
> y > y
> y B.y
B.y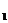 < y
< y < y
< y C.y
C.y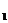 > y
> y > y
> y D.y
D.y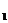 < y
< y < y
< y
6.如图,是一个正方体纸盒的展开图,若在其中的三个正方形A、B、C内分别填入适当的数,使得它们折成正方体后相对的面上的两个数为相反数,则填入正方形A、B、C内的三个数依次为( )

A.一2,0,1 B.0,一2,
7.不等式组 的解集为( )
的解集为( )
A.xㄒ3 B.x<一
8.小明本学期6次数学考试成绩依次是92分、87分、87分、72分、67分、75分,老师要求把六次测试的平均水平告知家长,小明应选择哪个值能使家长感觉他的成绩不错( )
A.平均数 B.中位数 C.极差 D.众数
9.口袋中放有2个黄球和2个黑球,每个球除颜色外都相同,从中任意摸出一个球,然后放回去再摸出一个球,摸出的球一个是黄球,一个是黑球的概率是( )
A. B.
B.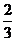 C.
C.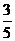 D.
D.
10.如图,小颖有一张矩形纸片经过三次对折后展开,发现第三次对折形成的折痕所围成的四边形是一种特殊的四边形,则这个四边形的对角线满足( )

A.互相平分 B.互相垂直 C.相等 D.互相垂直平分
11.已知x=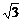 +1,y=
+1,y=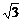 一1,那么(1+
一1,那么(1+ )(1一
)(1一 )的值为( )
)的值为( )
A.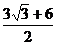 B.
B.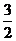 C.
C. D.
D.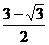
12.在圆锥高的中点处用平行于底面的平面去截圆锥,得到一个小圆锥,则小圆锥的表面积是原来表面积的( )
A. B.
B.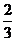 C.
C. D.
D.
二、填空题(本大题共有5个小题,每小题4分,共20分),要求填写最后结果)
13.一个凸多边形,除了一个内角外,其余各内角之和是2750°,则这个多边形的边数是_______.
14.如图,双曲线y=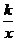 经过点(2,一6),点P为该双曲线上的一点,连接OP,OP与y轴所夹锐角为
经过点(2,一6),点P为该双曲线上的一点,连接OP,OP与y轴所夹锐角为 ,若sin
,若sin =
=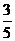 ,则点P的坐标为_________.
,则点P的坐标为_________.

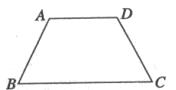
15.在等腰梯形ABCD中,AB=2,BC=4,∠B=45°,则该梯形的面积是_____________.
16.二次函数y=(x一3)(x+2)的图象的对称轴是_________________.
17.小王利用计算机设计一个个计算程序,输入和输出的数据如下表:
输入
…
l
2
3
4
5
…
输出
…


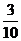
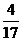

…
当输入数据是8时,输出的数是___________.
三、解答题(本题共8小题,共82分),解答应写出文字说明过程或演算步骤)
18.(本题满分8分)
 化简求值:(
化简求值:( )÷
)÷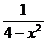 ,其中
,其中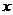 =
=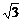 +2
+2
19.(本题满分8分)
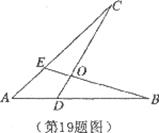
如图四个条件中,请你以其中两个为已知条件,第三个为结论,推出一个正确的命题(只需写出一种情况)写出证明过程
①AE=AD,②AB=AC,③OB=OC,④∠B=∠C.
20.(本题满分10分)
如图已知测速站P到公路L的距离PO为40米,一辆汽车在公路L上行驶,测得此车从A到B所用时间为2秒,并测得∠APO=60°,∠BPO=40°,计算此车从A到B的平均速度为每秒多少米?(结果保留四位有效数字)并判断此车是否超过了每秒22米的限制速度?

21.(本题满分10分)
某单位想为每名职工买一个电热水壶,采购员获得的信息是:甲、乙、丙三家商场均有销售同一牌子的电热水壶,并且各有自已的优惠办法.甲商场每个电热水壶定价100元,九折;买10个以上可以八折;买50个以上可以七折.乙商场每个电热水壶定价90元,九折;买10个以上可以八五折;买50个以上可以八折.丙商场每个电热壶定价为78元,不打折.请你为采购员设计方案,究竟在哪一家买更合算?
22.(本题满分10分)
如图,有两个可以自由转动的均匀转盘A、B,转盘A被均匀地分成4等份,每份分别标上l,2,3,4四个数字;转盘B被均匀地分成6等份,每份分别标上l,2,3,4,5,6六个数字,有人为甲、乙两人设计了一个游戏,其规则如下:

(1)同时自由转动转盘A与B;
(2)转盘停止后,指针各指向一个数字(如果指针恰好指在分格线上,那么重转一次,直到指针指向某一数字为止),用所指的两个数作乘积,如果得到的积是偶数,那么甲胜;如果得到的积是奇数,那么乙胜(如转盘A指向3,转盘B指针指向5,3×5=15,按规则乙胜).你认为这样的规则是否公平?请说明理由;如果不公平,请你设计一个公平的规则,并说明理由.
23.(本题满分10分)
一长为2的定线段AB为边作正方形ABCD,取AB的中点P,连接PD,在BA的延长线上取点F,使PF=PD,以AF为边作正方形AMEF,点M在AD边上(如图).

(1)求AM、MD的长;
(2)你能说明点M是线段AD的黄金分割点吗?
24.(本题满分12分)
已知抛物线y=ax +bx+c与y轴交于A(0,3),与x轴分别交于B(1,0)、C(5, 0)两点.
+bx+c与y轴交于A(0,3),与x轴分别交于B(1,0)、C(5, 0)两点.
(1)求此抛物线的解析式;
(2)若一个动点P自OA的中点M出发先到达x轴上的某点(设为点E),再到达抛物线的对称轴上某点(设为点F),最后运动到点A,求使点P运动的总路径最短的点E、点F的坐标,并求出这个最短总路径的长.
25.(本题满分14分)
(1)图①是一块直角三角形纸片.将该三角形纸片按如图①方法折叠,其中点A与点C重合,DE为折痕.试证明△CBE是等腰三角形;
(2)再将图①中的△CBE沿对称轴EF折叠(如图②).通过折叠,原三角形恰好折成两个重合的矩形,其中一个是内接矩形,另一个是拼合(指无缝无重叠)所成的矩形,我们称这样的两个矩形为“组合矩形”.你能将图③中的△ABC折叠成一个组合矩形吗?如果能折成,请在图③中画出折痕;
(3)请在图④的方格纸中画出一个斜三角形,同时满足下列条件:①折成的组合矩形为正方形;②顶点都在格点(各小正方形的顶点)上;
(4)有一些特殊的四边形,如菱形,通过折叠也能折成组合矩形(其中的内接矩形的四个顶点分别在原四边形的四条边上).请你进一步探究,一个非特殊的四边形(指除平行四边形、梯形外的四边形)满足何条件时,一定能折成组合矩形?
