2007年枣庄市滕州九年级三调考试
数学试题
亲爱的同学:
祝贺你完成了初中阶段的学习,现在是展示你的学习成果之时,你可以尽情地发挥,相信你能静心、尽心、诚实答卷。祝你成功!
注意:
1.答题前,必须把考号和姓名写在密封线内。
2.答题时,不得将答案写到密封线内。
3.选择题答案用2B铅笔涂在答题卡上,如不用答题卡,请将答案填在题后括号里。
4.考试时,不允许使用科学计算器。
一、选择题(本大题共12小题,共36分,在每小题给出的四个选项中,只有一项是正确的,请把正确的选项选出来。每小题选对得3分。选错、不选或选出的答案超过一个均记零分)。
1.世界文化遗产长城的总长度约为670000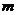 ,用科学记数法表示为(
)
,用科学记数法表示为(
)
A. B.
B.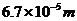
C.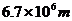 D.
D.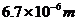
2.下列各图中,不是中心对称图形的是( )

3.下列调查方式合适的是( )
A.为了了解炮弹的杀伤力,采用普查的方式
B.为了了解全国中学生的睡眠状况,采用普查的方式
C.为了了解人们保护水资源的意识,采用抽样调查的方式
D.对载人航天器零部件的检查,采用抽样调查的方式
4.用两块边长为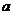 的等边三角形纸片拼成的四边形是(
)
的等边三角形纸片拼成的四边形是(
)
A.等腰梯形 B.正方形 C.矩形 D.菱形
5.若方程组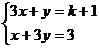 的解是
的解是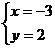 ,则
,则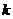 的取值(
)
的取值(
)
A.-4 B.
6.由一些大小相同的小正方体组成的几何体的三视图如下图所示,那么,组成这个几何体的小正方体有( )
A.6块 B.5块 C.4块 D.3块

7.如图,已知在⊙O中,BC是直径,
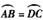 ,∠AOD=80°,则∠ABC等于( )
,∠AOD=80°,则∠ABC等于( )

A.40° B.65° C.100° D.105°
8.已知反比例函数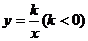 )的图像上有两点A(
)的图像上有两点A(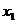 ,
, ),B(
),B(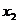 ,
,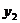 ),且
),且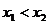 ,则
,则 的值是(
)
的值是(
)
A.正数 B.负数 C.非正数 D.不能确定
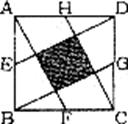
9.如图,E、F、G、H分别是正方形ABCD各边的中点,要使中间阴影部分小正方形的面积是5,那么大正方形的边长应该是( )
A.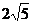 B.
B. C.5 D.
C.5 D.
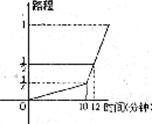
10.一名考生步行前往考场,10分钟走了总路程的 ,估计步行不能准时达,于是他改乘出租车赶往考场,他的行程与时间关系如图所示(假定总路程为1),则他到达考场所花的时间比一直步行提前了( )
,估计步行不能准时达,于是他改乘出租车赶往考场,他的行程与时间关系如图所示(假定总路程为1),则他到达考场所花的时间比一直步行提前了( )
A.20分钟 B.22分钟 C.24分钟 D.26分钟
11.正比例函数 的图像经过二、四象限,则抛物线
的图像经过二、四象限,则抛物线 的大致图像是(
)
的大致图像是(
)
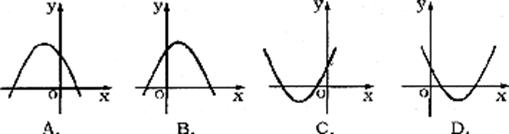
12.甲、乙两人比赛投篮球,以命中率(投进球数与投球次数的比值)来比较投球成绩的好坏,下表为两人投篮球的记录:
学 生
投进球数
没投进球数
投球次数
甲
10
5
15
乙
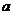

18
得知他们的成绩一样好,下面有四个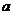 、
、 的关系式:
的关系式:
①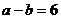 ; ②
; ② ;③
;③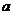 ∶
∶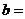 2∶1;④
2∶1;④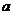 ∶
∶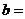 2∶3。 其中正确的是( )
2∶3。 其中正确的是( )
A.①②③ B.①③④ C.①②③④ D.②③④
二、填空题(本大题共6小题.共24分,只要求填写最后结果,每小题填对得4分)。
13.因式分解 ___________________.
___________________.
14.计算tan60°+2sin45°-2cos30°的结果是___________.
15.将矩形ABCD沿AE折叠,得到如图所示的图形,已知∠CED =60°,则∠EAD′=_______.
=60°,则∠EAD′=_______.

16.计算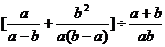 的值等于___________.
的值等于___________.
17.如图,以等腰三角形ABC的一腰AB为直径的⊙O交BC于点D,交AC于点G,连结AD,并过点D作DE⊥AC,垂足为E.根据以上条件写出三个正确结论(除AB=AC,AO=BO,∠∠ABC=∠ACB外)是:
(1) ___________;(2) ___________;(3) ___________.

18.观察图l至图5中小黑点的摆放规律,并按照这样的规律继续摆放,记第n个图中小黑点的个数为___________.

三、完成下列各题(本大题共7题,共60分,解答时要写出必要的文字说明、演算步骤或证明过程)。
19.(本题满分8分)
如图,两圆都以点O为圆心,直线分别交两圆于A、曰两点和C、D两点,请你找出线段AC和BD的数量关系,并证明你的结论。

20.(本题满分8分)
如图,有两个可以自由转动的均匀转盘A、B,转盘A被均匀地分成4等份,每份分别标上l、2、3、4 四个数字;转盘B被均匀地分成6等份,每份分别标上1、2、3、4、5、6 六个数字。有人为甲、乙两人设计了一个游戏,其规则如下:
(1)同时自由转动转盘A与B;
(2)转盘停止后,指针各指向一个数字(如果指针恰好指在分格线上,那么重转一次,直到指针指向某一数字为止),用所指的两个数作乘积,如果得到的积是偶数,那么甲胜;如果得到的积是奇数,那么乙胜(如转盘A指针指向3,转盘B指针指向5,3×5=15,按规则乙胜)。
你认为这样的规则是否公平?请说明理由;如果不公平,请你设计一个公平的规则。

21.(本题满分8分)
某企业投资112万元引进一条农产品加工生产线,若不计维修、保养等费用预计投产后每年可创利33万元,该生产线投产后从第一年到第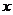 年的维修、保养费用累计为
年的维修、保养费用累计为 万元,且
万元,且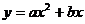 ,若第一年的维修保养费用为2万元,第二年为4万元。
,若第一年的维修保养费用为2万元,第二年为4万元。
(1)求 关于
关于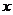 的解析式;
的解析式;
(2)设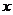 年后企业纯利润为
年后企业纯利润为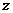 万元(纯利润=创利―维修、保养费用),投产后这个企业在第几年就能收回投资?
万元(纯利润=创利―维修、保养费用),投产后这个企业在第几年就能收回投资?
22.(本题满分8分)
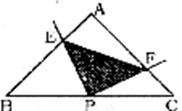
如图,在等腰Rt△ABC中,P是斜边BC的中点,以P为顶点的直角的两边分别与边AB,AC交于点E,F,连接EF。当∠EPF绕顶点P旋转时(点E不与A,B重合),△PEF也始终是等腰直角三角形,请你说明理由。
23.(本题满分8分)
电线杆上有一盏路灯O,电线杆与三个等高的标杆整齐划一地排列在马路的一侧,AB、CD、EF是三个标杆,相邻的两个标杆之间的距离都是
(1)请画出路灯O的位置和标杆EF在路灯灯光下的影子;
(2)求标杆EF的影长。

24.(本题满分10分)
下图是某次运动会开幕式上点燃火炬时在平面直角坐标系中的示意图,在O、A两个观测点,分别测得目标点火炬C的仰角分别为 ,
,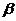 ,OA=
,OA=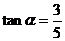 ,
,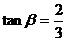 ,位于点O正上方
,位于点O正上方

(1)求火球运行轨迹的抛物线对应的函数解析式;
(2)说明按(1)中轨迹运行的火球能否点燃目标C。
25.(本题满分10分)
已知如图所示,直线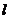 的解析式为
的解析式为 ,并且与
,并且与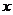 轴、
轴、 轴分别相交于点A、B。
轴分别相交于点A、B。
(1)求A、B两点的坐标;
(2)一个圆心在坐标原点、半径为1的圆,以0.4个单位/每秒的速度向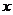 轴正方向运动,问什么时刻该圆与直线
轴正方向运动,问什么时刻该圆与直线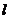 相切;
相切;
(3)在题(2)中,若在圆开始运动的同时,一动点P从B点出发,沿BA方向以0.5个单位/秒的速度运动,问在整个运动的过程中,点P在动圆的圆面(圆上和圆的内部)上一共运动了多少时间?