2007年枣庄市滕州市初中毕业考试
数学试题
本试卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分。第I卷1至2页.第Ⅱ卷3至8页。全卷满分150分。考试时间120分钟。
第I卷(选择题共60分)
注意事项:
1.答第I卷前,考生务必将自己的姓名、准考证号写在卷Ⅱ的密封线内;
2.每小题选出答案后,把答案填入卷Ⅱ的方格中;
3.考试结束后,监考人将第Ⅱ卷收回。
一、选择题:每小题4分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。
A.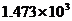 B.
B.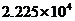 C.
C.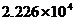 D.
D.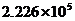
2.若方程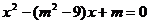 的两根互为相反数,则m等于
的两根互为相反数,则m等于
A.3 B.
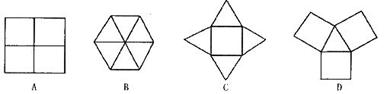
3.下面由正三角形和正方形拼成的图形中,是轴对称图形而不是中心对称图形的是
4.若 ,
,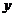 都是实数且满足
都是实数且满足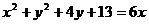 ,则
,则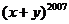 的值为
的值为
A.2007 B.-2007 C.1 D.-1
5.估算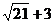 的值
的值
A.在5和6之间 B.在6和7之间
C.在7和8之间 D.在8和9之间
6.有13位同学参加跳远比赛。他们的成绩互不相同,取前6名同学进入决赛,某同学知道了自己的成绩后,还需知道这13位同学成绩的什么量,就能判断他能不能进入决赛
A.平均数 B.众数 C.最高分 D.中位数
7.双曲线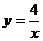 经过的点是
经过的点是
A.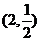 B.
B.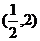 C.
C.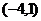 D.
D.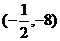
8.2006年的某个月份中有5个星期三,它们的日期之和为80(把日期作为一个数,例如26日看作26),那么这个月的18号是星期
A.一 B.二 C.四 D.五
9.已知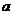 ,
,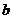 是一元二次方程
是一元二次方程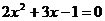 的两实根,则
的两实根,则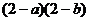 的值为
的值为
A. B.
B.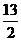 C.9 D.
C.9 D.
10.如图,O是原点,实数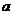 、
、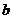 、
、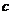 在数轴上对应的点分别为A、B、C,则下列结论错误的是
在数轴上对应的点分别为A、B、C,则下列结论错误的是
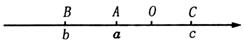
A.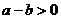 B.
B.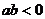 C.
C.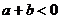 D.
D.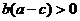
11.将进货单价为70元的某种商品按零售单价100元售出时,每天能卖出20个,若这种商品的零售单价在一定范围内每降价1元,其日销售量就增加1个,为了获取最大利润,则应降价
A.5元 B.10元 C.15元 D.20元
12.一次函数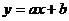 与二次函数
与二次函数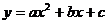 在同一坐标系的图像可能是
在同一坐标系的图像可能是

13.某商店售某种商品每件可获利m元,利润率为20%(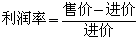 ),若这种商品的进价提高25%,而商店将这种商品的售价提高到每件仍可获利m元,则提价后的利润率为
),若这种商品的进价提高25%,而商店将这种商品的售价提高到每件仍可获利m元,则提价后的利润率为
A.20% B.16% C.18% D.25%
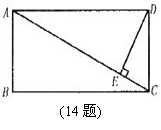
14.如图,在矩形ABCD中,DE⊥AC于点E,设∠ADE=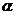 ,且
,且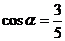 ,AB=4,则AD的长为
,AB=4,则AD的长为
A.3 B.4 C.5 D.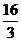

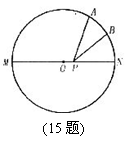

15.如图,点A是半圆上的一个三等分点,点P是直径MN上的一个动点,点B是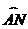 的中点。若已知⊙O的半径为
的中点。若已知⊙O的半径为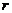 ,则AP+BP的最小值为
,则AP+BP的最小值为
A.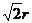 B.
B. C.
C.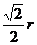 D.
D.
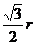
第Ⅱ卷 (非选择题共90分)
注意事项:
1.第Ⅱ卷共6页,用蓝色钢笔或圆珠笔直接答在试题卷上;
2.答卷前将密封线内的项目填写清楚.
二、填空题:本大题共5小题,每小题4分,共20分。把答案填在题中横线上。
16.函数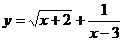 的自变量
的自变量 的取值范围是
。
的取值范围是
。
17.二次函数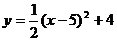 是由原来的二次函数向右平移4个单位,又向上平移5个单位得到的,则原二次函数的解析式为
。
是由原来的二次函数向右平移4个单位,又向上平移5个单位得到的,则原二次函数的解析式为
。
18.袋子里有2个红球、3个白球,每个球除颜色外都相同,任意摸出两个球均为红球的概率是 。
19.小勇在上午8时、9时30分、10时、12时四次到室外的阳光下观察向日葵的头茎随太阳转动的情况,无意中,他发现这四个时刻向日葵影子的长度各不相同,那么在这四个时刻中影子最长的是 。
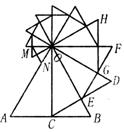
20.如右图,以等边△OAB的高OC为边向逆时针方向作等边△OCD,CD交OB于点E,再以OE为边向逆时针方向作等边△OEF,EF交OD于点G,再以OG为边向逆时针方向作等边△OGH,…,按此方法操作,最终得到△OMN,此时ON在OA上,若AB=2,则ON= 。
三、解答题:本大题共7小题。满分70分。解答应写出文字说明、证明过程或演算步骤。
21.(本小题满分8分)
计算: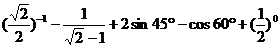
22.(本小题满分8分)
某甲鱼养殖专业户共养甲鱼200只,为了与客户签订购销合同,对自己所养甲鱼的总重量进行估计,随意捞了5只,称得重量如下:1.71 1.5 1.62 1.9(单位:千克)
(1)根据样本平均数估计甲鱼的总重量约是多少千克?
(2)如果甲鱼的市场价为每千克150元,那么该专业户卖出全部甲鱼的收入约为多少元?
23.(本小题满分8分)
已知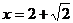 ,求代数式
,求代数式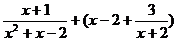 的值。
的值。
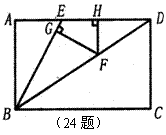
24.(本小题满分10分)
如图,E是矩形ABCD的边AD上一点,且∠EBD=∠EDB,F是对角线BD上任意一点,FG⊥BE,FH⊥AD,垂足分别是G、H。求证:FG+FH=AB。

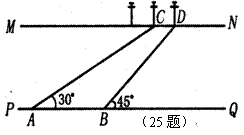

25.(本小题满分10分)
如图,河流的两岸PQ、MN互相平行,河岸MN上有一排间隔为50米的电线杆C,D,……,某人在河岸PQ的A处测得∠CAQ=30°,然后沿河岸走了110米到达B处,测∠DBQ=45°,求河流的宽度(结果保留根号)。
26.(本小题满分12分)
如图,AB是⊙O的直径,D是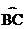 的中点,DE⊥AC交AC延长线于E,⊙O的切线BF交AD的延长线于点F。
的中点,DE⊥AC交AC延长线于E,⊙O的切线BF交AD的延长线于点F。
(1)求证:DE是⊙O的切线;
(2)若BF=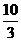 ,DE=3,求⊙O的半径。
,DE=3,求⊙O的半径。
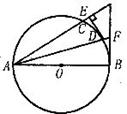
27.(本小题满分14分)
(1)求一次函数的表达式;
(2)若一开口向上的抛物线经过A、B、C三点,求此抛物线的函数表达式;
(3)过(2)中的A、B、C三点作△ABC,求tan∠ABC的值。