2006-2007学年度济宁市汶上县第二学期期中考试
八年级数学试题
一、选择题(请将正确答案的序号填在相应的括号内,每小题3分,共36分)
1.计算的结果是(x2y)-2.(2x-2y-3)-2的结果是( )
A.-4y4 B.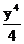 C.-4y5 D.
C.-4y5 D.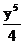
2.一辆汽车从甲地到乙地的速度为vl,从乙地原路返回甲地的速度为v2。则这辆汽车来回的平均速度是( )
A.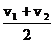 B.
B.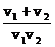 C.
C.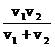 D.
D.
3.纳米是一种长度单位,1纳米=10
A.3.5×
C.3.5×10
4.计算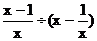 所得正确结果是( )
所得正确结果是( )
A.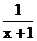 B.
B. D.-1
D.-1
5.已知点A (-3,4)在反比例函数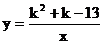 的图像上,那么下列各点在此函数图像上的是( )
的图像上,那么下列各点在此函数图像上的是( )
A.(3,4) B.(-3,-4) C.(3,-4) D.(-2,-6)
6.一双曲线的图象过点(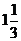 ,-3),则此双曲线的解析式为( )
,-3),则此双曲线的解析式为( )
A.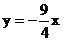 B.
B.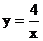 C.
C.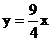 D.
D.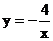
7.函数y=kx+l与函数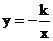 在同一坐标系中的大致图像是( )
在同一坐标系中的大致图像是( )

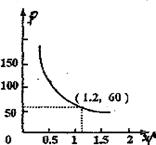 8.某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压P(KPa)是气体体积V(m3)的反比例函数,其图像如图所示,当气球内的气压大于105KPa时,气球将爆炸。为了安全起见,气体体积应( )
8.某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压P(KPa)是气体体积V(m3)的反比例函数,其图像如图所示,当气球内的气压大于105KPa时,气球将爆炸。为了安全起见,气体体积应( )
A.不大于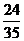 m3
m3
B.不小于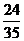 m3
m3
C.不大于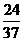 m3
m3
D.不小于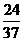 m3
m3
9.下列数组是勾股数的是( )
A.21,28,35 B.12,13,
10.一直角三角形的两直角边长分别为
A.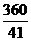 cm D.
cm D.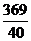 cm
cm
11.已知一个三角形的三边长a、b、c满足等式(a+b+c)(a+b-c)=2ab,则此三角形是( )
A.锐角三角形 B.直角三角形
C.等腰三角形 D.等边三角形
12.如图,P、Q为反比例函数的图像上任意两点,PP′、QQ′分别垂直x轴于点P′、Q′,则△PP′O与△QQ′O面积大小关系是( )
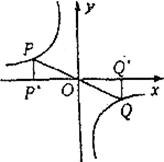
A.S△PP′=OS△QQ′O B.S△PP′O<S△QQ′O
C.S△PP′>OS△QQ′O D.无法确定
=、填空题(每小题3分.共24分)
13.当x_______时,分式 的值为0。
的值为0。
14.若关于x的分式方程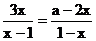 无解,则a=_________。
无解,则a=_________。
15.若反比例函数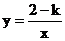 中,当x<0时,y随x的增大而减小,则k的取值范围是_____。
中,当x<0时,y随x的增大而减小,则k的取值范围是_____。
16.已知y1与x+1成正比例,比例系数为kl,y2与x成反比例,比例系数为k2,若函数y=y1+y2的图像过点(1,1)、(-1,3),则kl+k2=______。
17.如图所示的图形中,所有四边形都是正方形,三角形都是直角三角形,其中最大的正方形的边长为
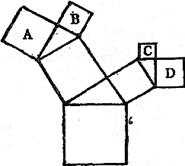
17题图 20题图
18.△ABC中,AB=
19.若点M(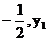 )、m(
)、m(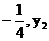 )、P(
)、P( )三点都在函数
)三点都在函数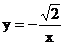 的图像上,则y1、y2、y3的大小关系为_________。
的图像上,则y1、y2、y3的大小关系为_________。
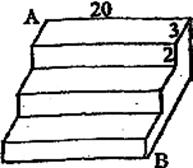
20.如图是一个三级台阶,它的每一级长、宽、高分别为20、3、2,A和B是这个台阶两个相对的端点,A点有一对蚂蚁。想到B点吃可口的食物,则蚂蚁沿着台阶面爬到B点最短路程是_______________。
三、解答题。(共60分)
21.计算(每小题5分,共10分)
(1)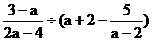
(2)
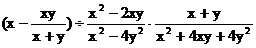
22.解方程。(每小题5分,共10分)
(1)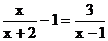
(2)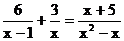
23.(本小题8分)
小明家离学校
24.(本题8分)
如图,在△ABC中,AC=8,BC=6,在△ABE中,DE为AB边上的高,DE=12,S△ABE=60。求∠C的度数。
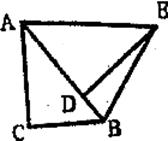
25.(本题共12分)
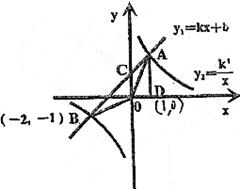
如图,已知一次函数yl=kx+b与反比例函数y2=k′的图像相交于A、B两点,AD上x轴,根据图中条件:
(1)求出两函数的解析式;
(2)求出△AOB的面积;
(3)根据图像写出一次函数yl的值大于反比例函数y2的值时的x值的取值范围。
26.(本题12分)
某厂从2002年开始投入技术改进资金,经技术改进后,其产品的生产成本不断降低,具体数据如下表:(12分)
年度
2002
2003
2004
2005
投入资金x(万元)
2.5
3
4
4.5
产品成本y(万元/件)
7.2
6
4.5
4
(1)请你认真分析表中数据,从你学过的一次函数和反比例函数中确定哪一种函数能表示其变化规律,说明确定是这种函数而不是另一种函数的理由,并求出它的函数解析式。
(2)按照这种变法规律,若2006年已投入改进资金5万元。
①预计生产成本每件比2005年低多少万元?
②如果打算在2006年把每件产品降低到3.2万元,则还需要投入技改资金多少万元?(结果精确到0.01万元)