1．下列各组数中、互为相反数的是（  ）

A. 2 与    B. 与1     C. -1与      D. 2与?-2?

2 ．从7¹ = 7 , 7² =49 ，7³=343,7⁴=2401,7⁵=16807…… 可以得出7 的正整数次幂的个位数的规律，从而可知7²⁰⁰⁷ 的个位数字是（  )
A. 1         B. 7          C.3           D. 9
3. 2006 年2 月12 日，我国发布了以“建设社会主义新农村”为主题的中央一号文件，文件指出：2006年至2010 年，我国将逐步把农村义务教育全面纳入公共财政保障体系，免除学杂费后，平均每个小学生每年可减负约140元，初中生减负约180 元，中央和地方各级财政5 年间将累计新增农村义务教育经费约2182 亿元．用科学记数法表示累计新增农村义务教育经费为(   )
A. 2.182 ×l0⁸      B. 21.82×10¹¹元
C. 2.182×10¹¹元    D. 2. 182×10¹²元
4．下表是体育彩票3D 游戏中奖号码，从第2006019 期到2006048 期和值（和值是指每期3D 开奖号码中三个数码的和）分布表：

则这30 天里中奖号码和值的众数，中位数分别是（   )

A. 8 和16

B. 8 和15

C. 15 和16

D. 15 和4

5. 不等式组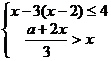无解,则 的取值范围是 （   ）

A. 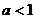   B.    C.     D.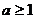  

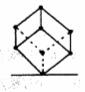
6. 如图所示，把一个正方体朝上立放，若此时该正方体上方亮一盏灯，则该正方体的影子（如图所示）应是（   ）

7. 六张完全相同的卡片上，分别画有等边三角形、正六边形、矩形、平行四边形、等腰梯形、菱形，现从中随机抽取一张，卡片上画的恰好既是轴对称图形又是中心对称图形的概率为 （   ）

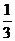A.       B.      C.      D.

8.已知点（）是反比例函数图像上一点，则此函数图像必经过点（  ）

A. (3,-5)     B. (5,-3)     C. (-3,5)     D. (3,5)

9.如图，小正方形的边长均为1，则下列图形中的三角形（阴影部分）与△ABC相似的是（   ）

10. 某种商品进价为800元，出售时标价为1200元，后来由于该商品积压，准备打折出售，要保持利润率不低于5％，该商店至多可打（   ）

A. 6 折      B. 7 折      C. 8 折     D. 8折

11．将一张正方形的纸片按下图所示的方式三次折叠，折叠后再按图所示沿MN 裁剪，则可得（    ）

A．多个等腰直角三角形
B．一个等腰直角三角形和一个正方形
C．四个相同的正方形
D．两个相同的正方形
12．如图，两块完全重合的正方形纸片，如果上面的一块绕正方形的中心O做0°～ 90°的旋转，那么旋转时露出的△ ABC 的面积（S ）随着旋转角度（n ）的变化而变化，下面表示S 与n 关系的图象大致是（   )

13．请写出一个顶点在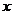 轴上，且开口方向向下的二次函数解析式                 。

14. ()的平方根是           
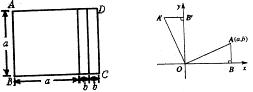
15．如图，由一个边长为的小正方形与两个长、宽分别为、 的小矩形拼接成矩形ABCD , 则整个图形可表达出一些有关多项式分解因式的等式，请你写出其中任意一个等式：

16．如图，将△AOB 绕点O逆时针旋转90°, 得到△A′OB′，若点A 的坐标为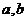（) ，则点A′的坐标为            ．
17．小红家春天粉刷房间，雇用了5 个工人，干了10 天完成；用了某种涂料150 升，每升32 元；每升涂料能粉刷1．最后结算工钱时，有以下几种方案：

方案一：按工算，每个工30 元；( 1 个工人干1 天是叫个工)；

方案二：按涂料费用算，涂料费用的30％作为工钱；

方案三：按粉刷面积算，每平方米付工钱12 元．

请你帮小红家出主意，选择方案     付钱最合算最省）.

18.如图，AB 、CD 是圆O 的直径，圆0 的半径为R , AB ⊥CD 以B 为圆心，以BC 为半径作。则与围成的新月形ACED 的面积为          平方单位。

19. （本题共8 分，每小题4 分）

（1）解方程：

（2）解不等式

20．（本小题满分8 分）

求 的值，其中

21. （本题满分10 分）

下面两幅统计图（如图l 、图2 ) ，反映了某市甲、乙两所中学学生参加课外活动的情况，请你通过图中信息回答下面的问题。

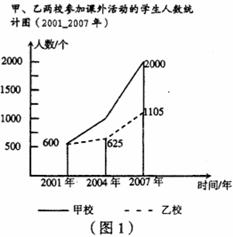
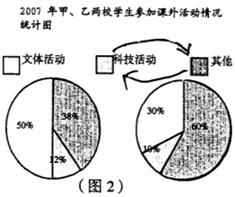
                                              甲                   乙

（1）通过对图1的分析，写出一条你认为正确的结论；

（2）通过对图的分析，写出一条你认为正确的结论；

（3）2007年甲、乙两所中学参加科技活动的学生人数共有多少？

22.（本题满10分）我们学过的确定物体位置的方法有平面直角坐标系法和方位角法，现在再给你介绍一种方法：如图① ，将射线OX 按逆时针方向绕O点旋转度，得到射线OY，如果P为射线OY上的一点，且OP＝，我们规定用（）P点位置。问题：

(1）在图② 中，如果点Q 在平面内的位置记为Q (8, 100°），那么OQ =      。∠XOQ =          

(2）在图③ 中，如果点A 、B 在平面内的位置分别记为A (4,45°）, B( ，75°）试求A 、B 两点间的距离．

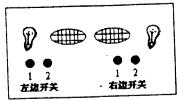
23. （本题满分8 分）依据闯关游戏规则，请你探究“闯关游戏”的奥秘：

(1) 用列表的方法表示所有可能的闯关情况；

(2）求出闯关成功的概率。

24.（本题满分10 分）如图，给出五个条件：① AE平分∠BAD ，② BE 平分∠ABC ，③ E 是CD 的中点，④ AE⊥EB ，⑤ AB = AD + BC
(l）请你以其中三个作为命题的条件，写出一个能推出AD//BC的正确命题，并加以说明；

(2）请你以其中三个作为命题的条件，写出一个不一定能推出AD//BC 的正确命题，并举例说明．

25. （本题满分12 分）春、秋季节，由于冷空气的入侵，地面气温急剧下降到0℃ 以下的天气现象称为“霜冻”。由霜冻导致植物生长受到影响或破坏现象称为霜冻灾害。某种植物在气温是0℃ 以下持续时间超过3 小时，即遭到霜冻灾害，需采取预防措施。下图是气象台某天发布的该地区气象信息，预报了次日0时～8时气温随着时间变化情况，其中0时～5时的图象满足一次函数关系，5 时～8 时的图象满足二次函数关系。请你根据图中信息，解答下列问题：

(1）求次日5 时的气温；
(2）求二次函数的解析式；

(3）针对这种植物判断次日是否需要采取防霜措施，并说明理由．（参考数据：）

26. （本题满分12 分）在一次课题学习中活动中，老师提出了如下一个问题：
点P 是正方形ABCD 内的一点，过点P 画直线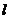 分别交正方形的两边于点M 、N ，使点P 是线段MN 的三等分点，这样的直线 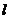能够画几条？
经过思考，甲同学给出如下画法：
如图1 ，过点P 画PE ⊥AB 于E ，在EB 上取点M 使EM＝2EA ，画直线MP 交AD 于N ，则直线MN 就是符合条件的直线 .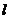
根据以上信息解决下列问题：
(1）甲同学的画法是否正确？请说明理由．

(2）在图（1）中，能否画出符合题目条件的直线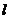？如果能，请直接在图1 中画出．

(3）如图2 , A₁、C₁ 分别是正方形ABCD的边AB、CD上的三等分点，且A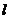₁C₁ //AD ．当点P 在线段A₁C₁上时能否画出符合题目条件的直线 ？如果能，可以画出几条？

(4）如图3 ，正方形ABCD 边界上的A₁ 、A₂、B₁、B₂ 、C₁、C₂、D₁、D₂ 都是所在边的三等分点．当点P 在正方形ABCD 内的不同位置时，试讨论，符合题目条件的直线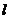 的条数的情况．