2006-2007学年度潍坊市昌邑第二学期期中考试
八年级数学试卷
说明:1、本试卷共2张8页。满分120分,考试时问120分钟。
2、用蓝、黑色钢笔或圆珠笔答卷,字迹清楚,卷面整洁。
3、请在密封线以内答题.
一、填空题(每空2分.共34分)
1、分式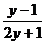 中,y________时.分式有意义.
中,y________时.分式有意义.
2、计算: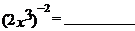 ,
,
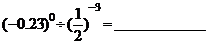
3、某种感冒病毒的直径是0.000 000
4、化简: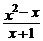 ÷
÷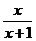 =_______________________.
=_______________________.
5、己知点M(1-a,2)在第二象限,则a的取值范围是____________?
6、若直线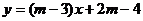 过原点,则直线解析式为_____________________
过原点,则直线解析式为_____________________
7、用一根长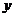 (cm)与腰长
(cm)与腰长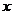 (cm)之间的函数关东式是_____________,自变量
(cm)之间的函数关东式是_____________,自变量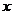 的取值范围是______________________?
的取值范围是______________________?
8、一次函数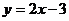 不经过第__________象限。
不经过第__________象限。
9、直线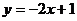 上的点A到x轴的距离为3,则点A的坐标是____________。
上的点A到x轴的距离为3,则点A的坐标是____________。
10、对于函数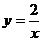 ,当
,当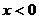 对,它的图象在第_________象限。
对,它的图象在第_________象限。
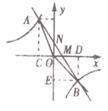
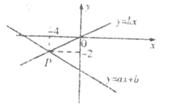
11、如图,已知函数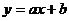 和
和 的图象交于点P,则根据图象可得:关于
的图象交于点P,则根据图象可得:关于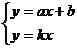 的二元一次方程组的解是_________________________。
的二元一次方程组的解是_________________________。
12、把“等腰梯形的两条对角线相等”改写成“如果……,那么……”的形式为_________
______________________________________
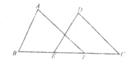
13、如图,AB=DE,BE=OF,若证△ABF≌△DEC,还需补充的一个条件____________或_____________________________
14.如果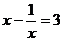 ,那么
,那么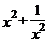 占的值为____________________________
占的值为____________________________
二、选择题(每小题3分,共30分)
1、给出下列说法
(1)因为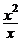 约分后得x,所以
约分后得x,所以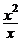 不是分式。
不是分式。
(2)分式是有理式
(3)分式的分子和分母都减去l,分式的值不变。
(4)分式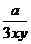 ,
, 的最简公分母是
的最简公分母是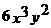 .其中说法正确的有:( )
.其中说法正确的有:( )
A.0个 B.1个 C.2个 D.3个
2、如果从一卷粗细均匀的电线上截取
A.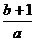 米 B.
米 B.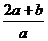 米 C.
米 C.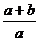 米 D.
米 D.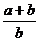 米
米
3、若关于x的方程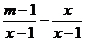 =0有增根.则m的值是( )
=0有增根.则m的值是( )
A.3 B.
4、当自变量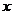 增大时.下列函数值反而减小的是( )
增大时.下列函数值反而减小的是( )
A.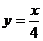 B.y=-3+4x
C.
B.y=-3+4x
C. 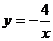 D.y=-3x
D.y=-3x
5、已知反比例函散的图象经过点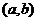 ,则它的图象一定也经过( )-
,则它的图象一定也经过( )-
A.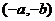 B.
B. C.
C.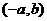 D
D 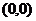
6、下列各点中,在函数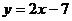 的图象上的是( )
的图象上的是( )
A.(2,3) B.(3,1) C.(0,一7) D、(-1,9)
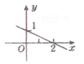
7、若函数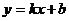 (k,b为常数)的图象如图所示,那么当
(k,b为常数)的图象如图所示,那么当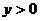 时,
时,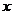 的取值范围是( )
的取值范围是( )
A.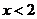 B.
B. 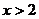 C.
C.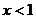 D.
D.
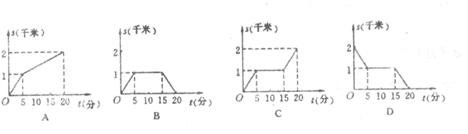
8、小明所在学校离家距离为
9、两个直角三角形全等的条件是( )
A.一条边对应相等 B.两条边对应相等
C.一锐角对应相等 D.两锐角对应相等
10、己知△ABC和△DEF中,∠B=∠E,∠C=∠F,只需满足下列条件的( )就能得到△ABC≌△DEF
A.AB=DE B.AC=DF C.BC=EF D.以上都正确
三、解答题(共56分)
1.小林家距离学校a千米,距离爸爸的单位b千米。小林骑自行车上学需要m分钟,爸爸开车上班需要n分钟,爸爸的速度是小林速度的多少倍?(3分)
2.计算:(1)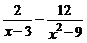 (4分)
(4分)
(2)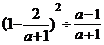
 (4分)
(4分)
3解方程: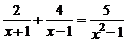 (6分)
(6分)
4.甲、乙两地相距390千米,新修的高速公路开通后。在甲、乙两地间行驶的长途客车平均车速提高了30%,所以从甲地到乙地的时问缩短了1.5小时,求原来的平均车速。(6分)
5.如图,已知AB=DC,AC=DB;求证:BE=CE(6分)

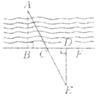
6要测量河两岸相对的两点A、B的距离,如图所示,可以在AB的垂线BF上取两点C、D,使CD=BC,再确定出BF的垂线DE,使A、C、E在一条直线上,这时测得DE的长就是AB的长,请说明这是为什么?(6分)
7.为了鼓励居民节约用水,某城市自来水公司实行分段收取水费,每户居民每月用水在10立方米以内,则每立方米收水费0.8元,若超过10立方米,则超过部分的水费按每立方米1.2元收费;
(1)请写出这个城市居民每月的水费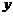 (元)与用水量
(元)与用水量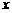 (立方米)之间的函数关系式;
(立方米)之间的函数关系式;
(2)该城市的居民李明家2月份和3月份分别交水费7.6元和11.6元,请你帮李明算一下他家这两个月的用水量分别是多少。(10分)
8.如图,已知一次函数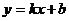 的图象与反比倒函数
的图象与反比倒函数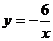 的图象交于A、B两点,且点A的横坐标和点B的纵坐标都是一2.
的图象交于A、B两点,且点A的横坐标和点B的纵坐标都是一2.
(1)求一次函数的解析式;
(2)求△AOB的面积。(11分)