2006-2007学年度泰安市上学期期末会考初二数学试题
(考试时间120分钟,满分120分)
注意事项:
1.本试题分第1卷和第Ⅱ卷两部分.第1卷2页为选择题共36分;第Ⅱ卷3至10页为非选择题,共84分,全卷满分120分.考试时间120分钟.
2.答第1卷前务必将自己的姓名、考号、考试科目涂写在答题卡上.考试结束,只收第Ⅱ卷和答题卡,不收第Ⅰ卷.
3.第1卷每题选出答案后,都必须用2B铅笔把答题卡上对应题目的答案标号(AB―CD)涂黑,如需改动,必须先用橡皮擦干净,再改涂其他答案,不能答在试题卷上.
第Ⅰ卷 (选择题共36分)
一、选择题(每小题3分.满分36分)
1.若一个直角三角形的三边长分别为3,4,x,则满足条件的x2的值为
A.5 B.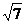 或5 C.25或7 D.16
或5 C.25或7 D.16
2.下列各组算式中,正确的是
A.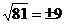 B.
B.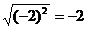 C.
C.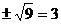 D.
D.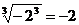
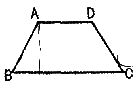
3.如图所示.等腰梯形的底角为45。,它的高恰好与上底长相等,若下底BC=9,那么梯形的腰长为
A.3 B.5 C.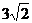 D.
D.
4.用两个形状和大小完全一样的直角三角形纸片,一定能拼成下列图形中的(不重叠,不留缝隙) ①等腰三角形 ②平行四边形 ③矩形 ④菱形 ⑤正方形
A.①②③ B.②③④ C.①③⑤ D.①②③④⑤
5.在第二象限内到X轴距离为3,到y轴距离为5的点的坐标为
A.(-5,3) B.(-3,5) C.(5,-3) D.(3,-5)
6.菱形的周长为20cm,一条对角线长为6cm,则另一条对角线的长为
A.4cm B.6cm C.8cm D.16cm
7.过点(2,3)的正比例函数的解析式是
A. B.
B.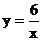 C.y=2x-1 D.
C.y=2x-1 D.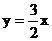
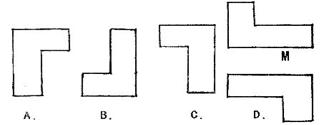
8.下列选项所对应的图形中,不能由图形M经过一次平移或旋转得到的是
9.二元一次方程组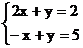 的解是
的解是
A.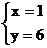 B.
B.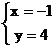 C.
C.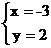 D.
D.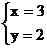
10.有l0个数据的平均数为12,另有20个数据的平均数为15,那么所有这30个数据的平均数是
A.12 B.15 C.13.5 D.14
11.能够密铺的正多边形组合是
A.正方形和正六边形 B.正方形和正八边形
C.正三角形和正八边形 D.正三角形和正十边形
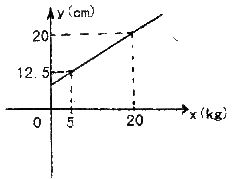
12.弹簧的长度与所挂物体的质量的关系为一次函数关系,如图所示,由图可知,不挂物体时弹簧的长度为
A.7cm B.8cm C.9cm D.10cm
第Ⅱ卷 (非选择题,共84分)
注意事项:
1.答卷前将密封线内的项目填写清楚.
2.第Ⅱ卷共8页,用蓝黑钢笔或圆珠笔直接答在试卷上.
二、填空题(每小题3分.满分21分)
13.若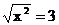 ,则X的值为______.
,则X的值为______.
14.某多边形的每个内角都等于1440,则这个多边形的边数为_____
15.数据8,9,9,8,10,8,9,9,8,10,7,9,9,8,10,7的众数是_____,中位数是_____,平均数是_____.
16.如果四边形ABCD是一个平行四边形,那么再加上条件_____,它就可变为菱形(只需填一个条件).
17.若平行四边形一个内角的平分线分一边为3cm,5cm两部分,则这个平行四边形的周长为_____cm.
18.一次函数y=-x+l与y=x-7的图象的交点坐标为_____.
19.□ABCD在坐标系内的位置如图所示,其中0点恰为□ABCD对角线的交点,若B点坐标为(-3,3),则D点坐标为_____

三、解答题(本大题满分63分)
20.(本大题满分12分)
(1)
(2) 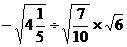
21.(本大题满分6分)
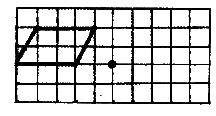
如图,已知平行四边形平移到某处后,又绕图中所给的点旋转了1800,所得图形恰好与初始图形重合,请说明平行四边形是怎么平移的.
22.(本大题满分8分)
某校为了了解本校中小学实施素质教育的情况,抽查了某校初一年级甲、乙两个班部分学生,了解他们在一周内(星期一至星期五)参加课外活动的次数情况,抽查结果如下图:

(1)在这次抽查中,甲班被抽查了______人,乙班被抽查了______人;
(2)在被抽查的学生中,甲班学生参加活动的平均次数为―次,乙班参加活动的平均次数为______次;
(3)根据以上信息用你学过的知识,估计甲、乙两班在开展课外活动方面哪个班更积极些?
(4)从图中你还能得到哪些信息?(写出一个即可).
23.(本大题满分8分)
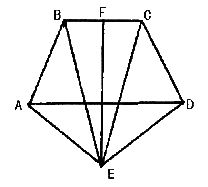
如图,在等腰梯形ABCD中,AB=CD,AD//BC,E是梯形外一点,且EA=ED,若F是BC的中点,判断EF与BC的位置关系,并说明理由.
24.(本大题满分7分)
某厂去年总产值比总支出多500万元,即利润为500万元,今年计划的总产值比总支出多950万元,已知今年计划总产值比去年增加15%,而计划总支出比去年减少10%,
求今年计划的总产值和总支出各为多少?
25.(本大题满分10分)
某农场20名职工承包了农场50亩土地,计划用来种植蔬菜,烟草或小麦,种这些作物每亩地所需职工数和产值预测如下表(要求每个人都有工作,每亩地都种上作物)
作物名称
每亩地需要职工数
每亩地预测产值
蔬菜
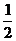
1100元
烟草
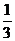
750元
小麦
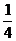
600元
(1)如果种植蔬菜X亩,烟草Y亩,根据题意,你能求出Y与x之间的关系式吗?它们是何种关系?
(2)若设预测总产值为W,请将W用含X的代数式表示出来.
(3)请设计出一种种植方案,使获得的利润最大,并求出这个最大值
26.(本大题满分12分)
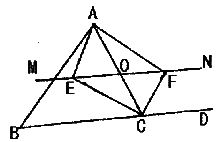
如图所示,△ABC中,点O是AC边上一动点,过点O作直线MN//BC,设MN交∠BCA的外角平分线于点F,交∠BCA的平分线于点E.
(1)说明EO=OF.
(2)当点O运动到何处时,四边形AECF是矩形?并说明理由.
(3)当△ABC满足什么条件时,四边形AECF是正方形?并说明理由.