2007年淄博市张店区初中毕业班第一次模拟考试
数学试题
一、选择题(第1-6小题,每小题各3分,第7-12小题,每小题各4分,共42分,请将正确选项的字母填在相应的空格内.)
1.方程组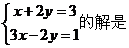
A. 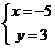 B.
B. 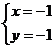 C.
C. 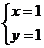 D.
D. 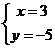
2.下列叙述正确的是
A.若ac=bc,则a=b B.若a2=b2,则a=b
C.若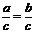 ,则a=b D.若|a|=|b|,则a=b
,则a=b D.若|a|=|b|,则a=b
3.将方程x2+4x+1=O配方后,原方程变形为
A.(x+2)2=3 B.(x+4)2=
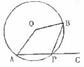 4.如图,图心角∠AOB=120°,P是
4.如图,图心角∠AOB=120°,P是 上任一点(不与A、B重合),点C在AP的延长线上,则∠BPC等于
上任一点(不与A、B重合),点C在AP的延长线上,则∠BPC等于
A.45° B.60° C.75° D.85°
5.若点P在第四象限内,且到x轴、y轴的距离分别是3和4,则点P的坐标为
A.(-4,3) B.(4,-3) C.(3,-4) D.(-3,4)
6.抛物线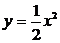 向左平移3个单位,再向下平移2个单位后,所得的抛物线的表达式是
向左平移3个单位,再向下平移2个单位后,所得的抛物线的表达式是
A.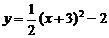 B.
B. 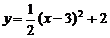
C. 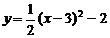 D.
D. 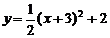
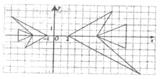 7.某学习小组在讨论“变化的鱼”时,知道大鱼与小鱼是位似图形(如图所示),则小鱼上的点(a,b)对应大鱼上的点
7.某学习小组在讨论“变化的鱼”时,知道大鱼与小鱼是位似图形(如图所示),则小鱼上的点(a,b)对应大鱼上的点
A.(
C.(-2b,
8.点P是△ABC中AB边上的一点,过点P作直线(不与直线AB重合)截△ABC使得的三角形与原三角形相似,满足这样条件的直线最多有
A.2条 B. 3条 C.4条 D.5条
9.半径为4的圆中,垂直平分半径的弦长是

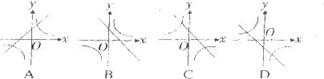
10.反比例函数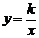 和一次函数y=kx-k在同一直角坐标系中的图象大致是
和一次函数y=kx-k在同一直角坐标系中的图象大致是
11.已知二次函数y=ax2+bx+c(a≠0)的图象如右图的所示,则下列结论:
①a-b+c>o,
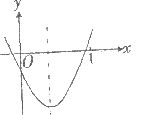 ②方程ax2+bx+c=0的两根之和大于零;
②方程ax2+bx+c=0的两根之和大于零;
③y随x的增大而增大;
④一次函数y=ax+bc的图象一定不过第二象限.
其中正确的个数是
A.1个 B.2个 C.3个 D.4个
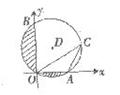 12.如图,在平面直角坐标系中,已知圆D经过原点O,与x轴、y轴分别交于A、B两点,B点坐标为(0,
12.如图,在平面直角坐标系中,已知圆D经过原点O,与x轴、y轴分别交于A、B两点,B点坐标为(0,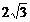 ),OC与圆D相交于点C,∠OCA=30°,则图中阴影部分的面积为
),OC与圆D相交于点C,∠OCA=30°,则图中阴影部分的面积为
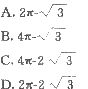
二 、 填空题(共5小 题,每小题4分,共20分)
13.函数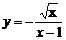 中自变量x的取值范围是________________
中自变量x的取值范围是________________
14.若关于x的方程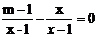 有增根,则m=_________________
有增根,则m=_________________
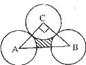 15.如图,在Rt△ABC中,∠C=90°,AC=BC=a,分别以A、B、C为圆心,以
15.如图,在Rt△ABC中,∠C=90°,AC=BC=a,分别以A、B、C为圆心,以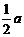 为半径画圆,三个圆与边AB所围成的阴影部分面积为_____________
为半径画圆,三个圆与边AB所围成的阴影部分面积为_____________
16. 一次函数y=4-3x利y=2x-1的图象交于一点,看直线y=ax-6经过它们的交点,则a的值为___________________________________________
17.在方格纸中,每个小格的顶点称为格点,以格点连线为边的三角形叫格点三角形。在如图5×5的方格中,作格点△ABC和△OAB相似(相似比不为1),则点C的坐 标是_____________________
标是_____________________
三、解答题(共7小题,共58分)
18.(本题满分6分)
为响应承办“绿色奥运”的号召,某中学初四(2)班计捌组织部分同学义务植树180棵,由于同学们参与的积极性很高,实际参加植树活动的人数比原计划增加了50%,结果每人比原计划少栽了2棵树,问实际有多少人参加了这次植树活动?
19.(本题满分8分)
为了培养同学们的综合实践能力,某数学老师让大家测量校园内的一棵高大松柏树,要测出它的高度,不能爬到树尖上去,也不能将树砍倒.老师提供的工具有小镜子和测量土地用的圈尺,请你写出两种测量方法,并加以论述,你是怎样计算出这棵大树的高度的(请画出示意图,并标明测量的数据,数据用a,b,……表示,并进行论证)。
20.(本题满分8分)
通过实验研究,专家们发现,初中学生听课的注意力指标是随着老师讲课时间变化而变化的,讲课开始时,学生的兴趣激增,中间有一段时间,学生的兴趣保持平稳的状态,随后开始分散.学生注意力的指标,y 随时间x(分)变化的图象如图所示(y越大注意力越集中).当0≤x≤10时,图象是抛物线的一部分,当10≤x≤20和20≤x≤40时,图象是线段.
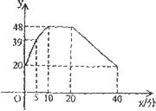 (1)当O≤x≤10时,求注意力的指标y随时间x变化的函数关系式,
(1)当O≤x≤10时,求注意力的指标y随时间x变化的函数关系式,
(2)现有一节课需要老师讲24分钟,何老师是否能经过适当的安排,使学生在听课时能够保证注意力的指标数一直不低于36?
21.(本题满分8分)
关于x的方程k2x2+2(k-1)x+1=0。有实数根.
(1)求k的取值范围;
(2)如果这个方程的两个实数根的倒数和的平方等于8,求k的值.
22.(本题满分8分)
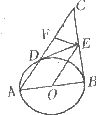 已知,以Rt△ABC的直角边AB为直径作圆O,与斜边AC交于点D,过点D作圆O的切线交BC边于点E.
已知,以Rt△ABC的直角边AB为直径作圆O,与斜边AC交于点D,过点D作圆O的切线交BC边于点E.
(1)如图,求证EB=EC=ED
(2)若∠DEF=∠C,EF交DC于点F
求证:BC2=4DF?DC
23.(本题满分8分)
某商场经营一批进价为a元/台的小加湿器,经调查得到下面表中的数据:
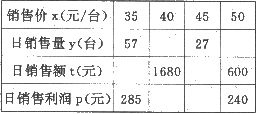
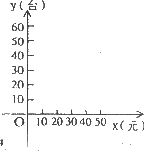
(1)请根据题意和表中已有的数据,在表中空白处填上适当的数;
(2)如图,在平面直角坐标系中,根据(1)中的数据,描出实数对(x,y)的对应点,根据你的猜测写出y与x的一个函数关系式;
(3)根据(2)中的关系写出p与x的函数关系式,并指出当销售价x为多少元时,才能获得最大的销售利润?
24.(本题满分12分)
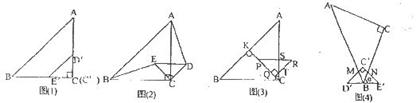
如图(1)是腰长分别是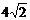 和2的两个等腰直角三角形ABC和C‘D‘E‘叠放在一起(C与C’重合).
和2的两个等腰直角三角形ABC和C‘D‘E‘叠放在一起(C与C’重合).
(1)固定△ABC,将△C‘D‘E‘绕点C顺时针旋转45°得到△CDE,如图(2),若连结BE、 AD,请你判断BE与AD的大小关系,并证明你的结论;
(2)延长CE交AB于K点,将图(2)中的△CDE在线段CK上沿着CK方向以每秒1个单位长度的速度平移,如图(3),将平移后的△CDE设为△PQR,设△PQR移动的时间为x秒,点P运动到K点停止,设△PQR与△AKC重叠的面积为y,求y与x的函数关系式,并写出自变量x的取值范围;
(3)将△D‘E‘C‘按如图(4)固定,将△ABC一锐角顶点B落在斜边E’D’的中点,然后绕B点逆时针旋转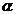 度,使边AB交D’C’于点M,边BC交E’C’于点N.
度,使边AB交D’C’于点M,边BC交E’C’于点N.
请你探究:图(4)的D’M?E’N的值是否随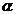 的变化而变化?如果没有变化,请求出D’M?E’N的值,并说明理由;如果有变化,也请说明理由.
的变化而变化?如果没有变化,请求出D’M?E’N的值,并说明理由;如果有变化,也请说明理由.