2006-2007学年度江苏省兴化市边城中学第一学期期中试卷
第一部分 选择题(36分)
一、选择题(下列各题所给答案中只有一个答案是正确的,每小题3分,共36分)
1.
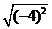 等于: ( )
等于: ( )
A. 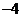 B.
B.
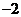
2. 一元二次方程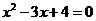 的根的情况是: ( )
的根的情况是: ( )
A. 有两个不相等的实数根 B. 有两个相等的实数根
C. 有一个实数根 D. 没有实数根
3. 如图,△ABC的3个顶点都在⊙O上,∠ACB = 40°,则∠AOB的度数是( )
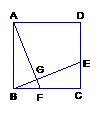
 A.
20°
B. 40°
C. 80°
D. 100°
A.
20°
B. 40°
C. 80°
D. 100°
第3题 第6题 第7题
4.
已知两圆的半径分别是方程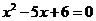 的两根,圆心距是5,则这两个圆的位置关系是: ( )
的两根,圆心距是5,则这两个圆的位置关系是: ( )
A. 外离 B. 外切 C. 相交 D. 内切
5. 李老师对学生小明一学期中的10次数学考试成绩进行分析,判断他的数学成绩是否稳定,则李老师需要知道该同学这10次考试成绩的: ( )
A. 众数 B. 方差 C. 平均数 D. 中位数
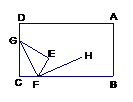
6.
如图:将一张矩形纸片ABCD的角C沿着GF折叠(F在BC边上,不与B、C重合)使得C点落在矩形ABCD内部的E处,FH平分∠BFE,则∠GFH的度数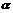 满足:
满足:
A. 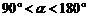 B.
B.
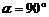 ( )
( )
C. 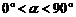 D.
D.
 随着折痕位置的变化而变化
随着折痕位置的变化而变化
7. 如图,在正方形ABCD中,点E、F分别在CD、BC上,且BF=CE,连结BE、AF相交于点G,则下列结论:①BE=AF;②∠DAF=∠BEC;③∠AFB+∠BEC=900;④AF⊥BE中正确的有 ( )
A. 1个 B. 2个 C. 3个 D. 4个
8. 如图是一个利用四边形的不稳定性制作的菱形晾衣架。已知其中每个菱形的边长为
A. 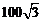 cm
cm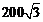 cm2
cm2
 |

第8题 第11题
9. 已知,E、F、G、H分别是四边形ABCD四条边的中点,要使四边形EFGH为矩形,四边形ABCD应具备的条件是 ( )
A. 一组对边平行而另一组对边不平行 B. 对角线相等
C. 对角线互相垂直 D. 对角线互相平分
10. 半径分别是2,4,6的三圆两两外切,那么以这三个圆的圆心为顶点的三角形的形状
是: ( )
A. 钝角三角形 B. 等腰三角形 C. 锐角三角形 D. 直角三角形
11. PA、PB切⊙O于A、B,C为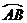 上一点,过C作⊙O的切线交PA、PB于M、N,若△PMN的周长为
上一点,过C作⊙O的切线交PA、PB于M、N,若△PMN的周长为
A.
12. 下列说法正确的个数是: ( )
① 同圆中,相等的圆心角所对的弧是等弧。
② 90°的角所对的弦是直径。
③ 圆的切线垂直于经过切点的半径。
④ 到三角形三边所在直线距离相等的点有且只有一个。
A. 1个 B. 2个 C. 3个 D. 4个
第二部分 非选择题(114分)
二、填空题(每空3分,共24分)
13. 若代数式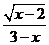 有意义,则
有意义,则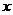 的取值范围是___________________。
的取值范围是___________________。
14. 请写出一个以2和3为根的一元二次方程(要求二次项系数为1)________________。
15. 一组数据0,1,2,3,4的标准差是_________________。
16. △ABC中,AB = 12,BC = 10,AC = 8,D、E、F分别是BC、CA、AB的中点,则△DEF的周长是______________。
17. 某商品经过连续两次降价,价格下降了19%,则平均每次降低的百分率是_________。
18. 如图,∠AOB = 900,将三角尺的直角顶点P,置于∠AOB的平分线OC上,让三角尺绕点P旋转,设三角尺的两直角边与∠AOB的两边分别交于E、F,请写出一个利用上述所有条件推出的一个正确结论(不再标注其它字母)_____________________。
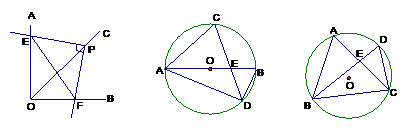 19.
如图,AB是⊙O的直径,弦AB、CD相交于E,∠ACD = 600,∠ADC = 500,则∠CEB = __________。
19.
如图,AB是⊙O的直径,弦AB、CD相交于E,∠ACD = 600,∠ADC = 500,则∠CEB = __________。
第18题 第19题 第20题
20. △ABC内接于⊙O,D为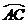 的中点,BD交AC于点E,若DC = 4,DB = 8,则
的中点,BD交AC于点E,若DC = 4,DB = 8,则
DE=____________。
三、解答题:
21. 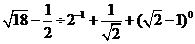 (8分)
(8分)
22. 先化简后求值:
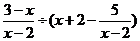 ,其中
,其中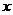 是方程
是方程 的根。 (8分)
的根。 (8分)
23.将进货单价为40元的商品按50元售出时,能卖出500个,已知这种商品每涨价0.1元时,其销量就减少1个,问:为了赚得9000元的利润,售价应定为多少?这时应进货多少个? (9分)
24. 如图,已知菱形ABCD,AE⊥BC于E,AF⊥CD于F。
(1) 求证:CE = CF;
(2) 若菱形边长为8,E是BC的中点,求菱形的面积。 (10分)
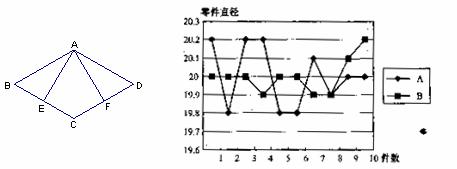
25. 如图,AB是⊙O的直径,PB与⊙O相切于点B,弦AC//OP。
(1) 求证:PC是⊙O的切线;
(2) 若BC = 8,AB = 10,求BP的长。 (10分)
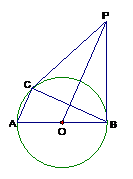
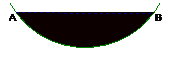
26. 某居民小区一处圆柱形的输水管道破裂,维修人员为更换管道,需确定管道圆形截面的半径,下图是水平放置的破裂管道有水部分的截面。
(1) 请你补全这个输水管道的圆形截面;
(2) 若这个输水管道有水部分的水面宽AB =
27. 某校为选派一名学生参加全市实践活动技能竞赛,分别对A、B两位同学加工的直径为
根据测试得到的有关数据,解答下列问题:
平均数
方差
完全符合要求的个数
A
20
0.026
2
B
20
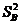
5
(1) 考虑平均数与完全符合要求的个数,你认为谁的成绩好些;
(2) 计算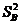 的大小,考虑平均数与方差,说明谁的成绩好些;
的大小,考虑平均数与方差,说明谁的成绩好些;
(3) 由图中折线走势及竞赛中加工零件个数远远超过10个的实际情况下,你认为派谁去参加较合适?说明你的理由。 (10分)
28. 矩形ABCO的面积为10,OA比OC大3,E为BC的中点,以OE为直径的⊙O'交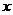 轴于D,DF⊥AE于F。
轴于D,DF⊥AE于F。
(1) 求OA、OC的长。
(2) 求DF长;
(3)
P为边BC上一动点,设△ABP的面积为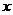 ,△OPC的面积为
,△OPC的面积为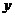 ,求
,求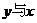 的函数关系式,并写出
的函数关系式,并写出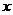 的取值范围。
的取值范围。
(4) 直线BC上是否存在点Q,使∠AQO = 90°,若存在,求出Q点坐标,若不存在,请说明理由。
(12分)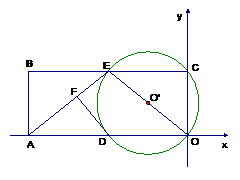
29. 如图(1),正△ABC和正△FDE,F与B重合,AB与FD在一条直线上。
(1) 若将△FDE绕点B旋转一定角度(如图2),试说明CD = AE;
(2)
已知AB = 6,DE =  ,把图(1)中的△FDE绕点B逆时针方向旋转90°(如图3),试判断四边形EBDC的形状,并说明你的理由;
,把图(1)中的△FDE绕点B逆时针方向旋转90°(如图3),试判断四边形EBDC的形状,并说明你的理由;
(3)
若把图(1)中的正△FDE沿BA方向平移(如图4),连结AE、BE,已知正△ABC和正△FDE的边长分别是 cm,问在平移过程中, △ABE是否会成为等腰三角形?若能,直接写出FB的值;若不能,说明理由。
(13分)
cm,问在平移过程中, △ABE是否会成为等腰三角形?若能,直接写出FB的值;若不能,说明理由。
(13分)
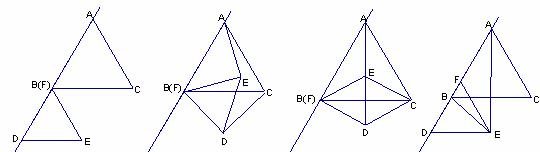
图1 图2 图3 图4